
Όριο ολοκληρώματος
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
- Tolaso J Kos
- Δημοσιεύσεις: 5237
- Εγγραφή: Κυρ Αύγ 05, 2012 10:09 pm
- Τοποθεσία: Λάρισα, Βαρκελώνη
- Επικοινωνία:
Όριο ολοκληρώματος
Να υπολογιστεί το παρακάτω όριο:


Η φαντασία είναι σημαντικότερη από τη γνώση !


Λέξεις Κλειδιά:
-
Λάμπρος Κατσάπας
- Δημοσιεύσεις: 838
- Εγγραφή: Σάβ Ιουν 17, 2017 10:17 pm
- Τοποθεσία: Αθήνα
Re: Όριο ολοκληρώματος
Θεωρούμε την
 και το ολοκλήρωμα γράφεται
και το ολοκλήρωμα γράφεται  .
. Με την αλλαγή μεταβλητής
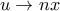 πάμε στο
πάμε στο  .
. Τώρα σπάμε το
![[0,n] [0,n]](/forum/ext/geomar/texintegr/latexrender/pictures/f0eb94d54e8e6126be266c0715815198.png) σε διαστήματα μήκους
σε διαστήματα μήκους  (στο τέλος περισσεύει ένα διάστημα μήκους
(στο τέλος περισσεύει ένα διάστημα μήκους ![n-\left [ \frac{n}{\pi } \right ]\pi <\pi. n-\left [ \frac{n}{\pi } \right ]\pi <\pi.](/forum/ext/geomar/texintegr/latexrender/pictures/a3e21ffeecb3bad36cbab44d4b93c468.png) )
) To τελευταίο ολοκλήρωμα γράφεται τώρα
![\displaystyle \frac{1}{n}\left (\sum_{k=0}^{\left [ \frac{n}{\pi } \right ]}\int_{k\pi} ^{(k+1)\pi } \ f\left (\frac{x}{n} \right )|\sin x|\, \mathrm{d}x+\int_{\left [ \frac{n}{\pi } \right ]\pi } ^{n } \ f\left (\frac{x}{n} \right )|\sin x|\, \mathrm{d}x \right ) \displaystyle \frac{1}{n}\left (\sum_{k=0}^{\left [ \frac{n}{\pi } \right ]}\int_{k\pi} ^{(k+1)\pi } \ f\left (\frac{x}{n} \right )|\sin x|\, \mathrm{d}x+\int_{\left [ \frac{n}{\pi } \right ]\pi } ^{n } \ f\left (\frac{x}{n} \right )|\sin x|\, \mathrm{d}x \right )](/forum/ext/geomar/texintegr/latexrender/pictures/f0b3978ef512f22381cd552f6218daaa.png)
![\displaystyle \frac{1}{n}\sum_{k=0}^{\left [ \frac{n}{\pi } \right ]}\int_{k\pi} ^{(k+1)\pi } \ f\left (\frac{x}{n} \right )|\sin x|\, \mathrm{d}x+ \frac{1}{n}\int_{\left [ \frac{n}{\pi } \right ]\pi } ^{n } \ f\left (\frac{x}{n} \right )|\sin x|\, \mathrm{d}x \right )=A+B. \displaystyle \frac{1}{n}\sum_{k=0}^{\left [ \frac{n}{\pi } \right ]}\int_{k\pi} ^{(k+1)\pi } \ f\left (\frac{x}{n} \right )|\sin x|\, \mathrm{d}x+ \frac{1}{n}\int_{\left [ \frac{n}{\pi } \right ]\pi } ^{n } \ f\left (\frac{x}{n} \right )|\sin x|\, \mathrm{d}x \right )=A+B.](/forum/ext/geomar/texintegr/latexrender/pictures/695ade8c894286ec582ee48aa4762ad4.png)
Ξεφορτωνόμαστε τώρα το απόλυτο ως εξής:
Με
 έχουμε
έχουμε 
Επίσης, επειδή η
 είναι γνησίως φθίνουσα, έχουμε
είναι γνησίως φθίνουσα, έχουμε![\displaystyle nB =\int_{\left [ \frac{n}{\pi} \right ]\pi}^{n} f\left ( \frac{x}{n} \right ) \left | \sin x \right |\, \mathrm{d}x <\int_{\left [ \frac{n}{\pi} \right ]\pi}^{n} f(0) \left | \sin x \right |\, \mathrm{d}x<\int_{0}^{\pi} \sin x \, \mathrm{d}x=2. \displaystyle nB =\int_{\left [ \frac{n}{\pi} \right ]\pi}^{n} f\left ( \frac{x}{n} \right ) \left | \sin x \right |\, \mathrm{d}x <\int_{\left [ \frac{n}{\pi} \right ]\pi}^{n} f(0) \left | \sin x \right |\, \mathrm{d}x<\int_{0}^{\pi} \sin x \, \mathrm{d}x=2.](/forum/ext/geomar/texintegr/latexrender/pictures/f40c5d58eeb31875f2972e0946b96449.png)
Συνεπώς
 .
.Δείχνουμε τέλος ότι
![\displaystyle A=\int_{0} ^{\pi }\frac{1}{n}\sum_{k=0}^{\left [ \frac{n}{\pi } \right ]} \ f\left (\frac{x+k\pi}{n} \right )\sin x\, \mathrm{d}x\rightarrow \int_{0} ^{\pi }\left ( \frac{1}{\pi}\int_{0}^{1}f(x)\, \mathrm{d}x \right )\sin x\, \mathrm{d}x=\frac{1}{2}. \displaystyle A=\int_{0} ^{\pi }\frac{1}{n}\sum_{k=0}^{\left [ \frac{n}{\pi } \right ]} \ f\left (\frac{x+k\pi}{n} \right )\sin x\, \mathrm{d}x\rightarrow \int_{0} ^{\pi }\left ( \frac{1}{\pi}\int_{0}^{1}f(x)\, \mathrm{d}x \right )\sin x\, \mathrm{d}x=\frac{1}{2}.](/forum/ext/geomar/texintegr/latexrender/pictures/dc5ab286f9fe92452af092777b76c11e.png)
Γι'αυτό θα δείξουμε ότι
![\displaystyle \frac{1}{n}\sum_{k=0}^{\left [ \frac{n}{\pi } \right ]} \ f\left (\frac{x+k\pi}{n} \right )\rightarrow \frac{1}{\pi}\int_{0}^{1}f(x)\, \mathrm{d}x \displaystyle \frac{1}{n}\sum_{k=0}^{\left [ \frac{n}{\pi } \right ]} \ f\left (\frac{x+k\pi}{n} \right )\rightarrow \frac{1}{\pi}\int_{0}^{1}f(x)\, \mathrm{d}x](/forum/ext/geomar/texintegr/latexrender/pictures/13fbf369a21f36d61e4f7893fb2e85ca.png) ομοιόμορφα στο
ομοιόμορφα στο ![[0,\pi]. [0,\pi].](/forum/ext/geomar/texintegr/latexrender/pictures/d1adee7c964715df2e19777eab1c612f.png)
Πράγματι, για κάθε
![x \in[0,\pi] x \in[0,\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/5bf1a9d0ca63a23bd851de2a28ee76a5.png) , επειδή η
, επειδή η  είναι γνησίως φθίνουσα παίρνουμε
είναι γνησίως φθίνουσα παίρνουμε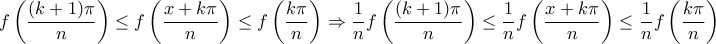
και
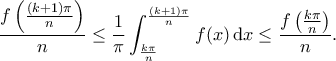
Άρα

Αθροίζοντας τις τελευταίες για
![k=0,1,...,\left [ \frac{n}{\pi} \right ] k=0,1,...,\left [ \frac{n}{\pi} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/294e9492f654f47416a0c8be56cca611.png) παίρνουμε
παίρνουμε ![\displaystyle \frac{1}{n}f\left ( \frac{(\left [ \frac{n}{\pi} \right ]+1)\pi}{n} \right )-\frac{1}{n}f\left ( 0\right )\leq \frac{1}{\pi}\int_{0}^{\frac{(\left [ \frac{n}{\pi} \right ]+1)\pi}{n}}f(x)\,\mathrm{d}x - \frac{1}{n}\sum_{k=0}^{\left [ \frac{n}{\pi} \right ]}f\left ( \frac{x+k\pi}{n} \right )\leq \frac{1}{n}f\left ( 0 \right )-\frac{1}{n}f\left ( \frac{(\left [ \frac{n}{\pi} \right ]+1)\pi}{n} \right ) \displaystyle \frac{1}{n}f\left ( \frac{(\left [ \frac{n}{\pi} \right ]+1)\pi}{n} \right )-\frac{1}{n}f\left ( 0\right )\leq \frac{1}{\pi}\int_{0}^{\frac{(\left [ \frac{n}{\pi} \right ]+1)\pi}{n}}f(x)\,\mathrm{d}x - \frac{1}{n}\sum_{k=0}^{\left [ \frac{n}{\pi} \right ]}f\left ( \frac{x+k\pi}{n} \right )\leq \frac{1}{n}f\left ( 0 \right )-\frac{1}{n}f\left ( \frac{(\left [ \frac{n}{\pi} \right ]+1)\pi}{n} \right )](/forum/ext/geomar/texintegr/latexrender/pictures/e6de8b6abbbd349138d6f7ac5292b0a2.png)
και παίρνοντας
 έχουμε το ζητούμενο.
έχουμε το ζητούμενο.H απόδειξη έχει ολοκληρωθεί.
τελευταία επεξεργασία από Λάμπρος Κατσάπας σε Πέμ Ιούλ 11, 2019 10:26 pm, έχει επεξεργασθεί 2 φορές συνολικά.
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Όριο ολοκληρώματος
Θα δείξω κάτι γενικότερο
Αν
![f:[0,1]\rightarrow \mathbb{R} f:[0,1]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/061d8197e20e9853f16cbd308ba889c8.png)
Lebesgue ολοκληρώσιμη τότε

Από σειρές Fourier έχουμε ότι για

είναι

Επειδή η σειρά συγκλίνει ομοιόμορφα είναι
 (1)
(1)Χρησιμοποιώντας ότι

και το Riemann-Lebesgue
παίρνοντας
 στην (1) έχουμε το ζητούμενο.
στην (1) έχουμε το ζητούμενο.Re: Όριο ολοκληρώματος
Από την σκοπιά της Fourier γενικεύεται και άλλο. Συγκεκριμένα, έστωΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Πέμ Ιούλ 11, 2019 5:11 pmΘα δείξω κάτι γενικότερο
Αν
Lebesgue ολοκληρώσιμη τότε
Από σειρές Fourier έχουμε ότι για
είναι
Επειδή η σειρά συγκλίνει ομοιόμορφα είναι
(1)
Χρησιμοποιώντας ότι
και το Riemann-Lebesgue
παίρνονταςστην (1) έχουμε το ζητούμενο.
 τότε:
τότε: 
Όπου
 ο μοναδιαιος κύκλος, τα ολοκληρώματα είναι Lebesgue.
ο μοναδιαιος κύκλος, τα ολοκληρώματα είναι Lebesgue.Αρμενιάκος Σωτήρης
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Όριο ολοκληρώματος
Μπράβο Σωτήρη.sot arm έγραψε: ↑Πέμ Ιούλ 11, 2019 6:23 pmΑπό την σκοπιά της Fourier γενικεύεται και άλλο. Συγκεκριμένα, έστωΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Πέμ Ιούλ 11, 2019 5:11 pmΘα δείξω κάτι γενικότερο
Αν
Lebesgue ολοκληρώσιμη τότε
Από σειρές Fourier έχουμε ότι για
είναι
Επειδή η σειρά συγκλίνει ομοιόμορφα είναι
(1)
Χρησιμοποιώντας ότι
και το Riemann-Lebesgue
παίρνονταςστην (1) έχουμε το ζητούμενο.
τότε:
Όπουο μοναδιαιος κύκλος, τα ολοκληρώματα είναι Lebesgue.
Αν και γνώριζα την σχέση δεν πήγε το μυαλό μου σε αυτήν.
Αν την προσαρμόσουμε στο
![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) το αποτέλεσμα γίνεται τετριμμένο.
το αποτέλεσμα γίνεται τετριμμένο.Αποδίδεται στον Fejer και ισχύει ακόμα αν

με

Η απόδειξη της είναι σχετικά εύκολη.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 16 επισκέπτες

 Αν και η απόδειξη που έχω κάνει είναι σχεδόν στοιχειώδης (μόνο ομοιόμορφη
Αν και η απόδειξη που έχω κάνει είναι σχεδόν στοιχειώδης (μόνο ομοιόμορφη