 , παίρνουμε σημείο
, παίρνουμε σημείο  και φέρουμε τις προβολές
και φέρουμε τις προβολές  στις πλευρές
στις πλευρές  αντίστοιχα.
αντίστοιχα. Αν
 και
και  , να βρείτε το μήκος του τμήματος
, να βρείτε το μήκος του τμήματος 
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 , παίρνουμε σημείο
, παίρνουμε σημείο  και φέρουμε τις προβολές
και φέρουμε τις προβολές  στις πλευρές
στις πλευρές  αντίστοιχα.
αντίστοιχα.  και
και  , να βρείτε το μήκος του τμήματος
, να βρείτε το μήκος του τμήματος 
Καλησπέρα σε όλους!Μιχάλης Νάννος έγραψε: ↑Τετ Ιουν 26, 2019 4:07 pmshape.pngΣτο εσωτερικό ισοπλεύρου τριγώνου, παίρνουμε σημείο
και φέρουμε τις προβολές
στις πλευρές
αντίστοιχα.
Ανκαι
, να βρείτε το μήκος του τμήματος

 είναι η πλευρά του ισοπλεύρου, τότε με τους συμβολισμούς του σχήματος είναι:
είναι η πλευρά του ισοπλεύρου, τότε με τους συμβολισμούς του σχήματος είναι:

 και
και 
ΚαλησπέραΜιχάλης Νάννος έγραψε: ↑Τετ Ιουν 26, 2019 4:07 pmshape.pngΣτο εσωτερικό ισοπλεύρου τριγώνου, παίρνουμε σημείο
και φέρουμε τις προβολές
στις πλευρές
αντίστοιχα.
Ανκαι
, να βρείτε το μήκος του τμήματος


 ,
,
 θεωρώ σημείο
θεωρώ σημείο  και κατασκευάζω δύο ημιευθείες
και κατασκευάζω δύο ημιευθείες  προς το αυτό μέρος της ευθείας και σχηματίζοντας από
προς το αυτό μέρος της ευθείας και σχηματίζοντας από  .
. θεωρώ σημείο
θεωρώ σημείο  για το οποίο
για το οποίο  .
.  . κάθετη στο
. κάθετη στο  επί την
επί την  και μεταξύ αυτής και της
και μεταξύ αυτής και της  τοποθετώ τμήμα μήκους
τοποθετώ τμήμα μήκους  και κάθετο στην
και κάθετο στην  .
.  . . Η παράλληλη προς την
. . Η παράλληλη προς την  από το
από το  τέμνει την
τέμνει την  στο
στο 
 στην
στην  την τέμνει στο
την τέμνει στο  . Στην δε προέκταση της
. Στην δε προέκταση της  θεωρώ τμήμα
θεωρώ τμήμα  , ώστε :
, ώστε : 
 , παράλληλη στην ευθεία
, παράλληλη στην ευθεία  που συναντά τη
που συναντά τη  στο
στο  .
. το σημείο τομής της
το σημείο τομής της 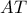 με την
με την  . Τα
. Τα 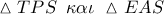 είναι της μορφής :
είναι της μορφής : και αφού
και αφού 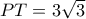 θα είναι :
θα είναι : 

ΈστωΜιχάλης Νάννος έγραψε: ↑Τετ Ιουν 26, 2019 4:07 pmshape.pngΣτο εσωτερικό ισοπλεύρου τριγώνου, παίρνουμε σημείο
και φέρουμε τις προβολές
στις πλευρές
αντίστοιχα.
Ανκαι
, να βρείτε το μήκος του τμήματος

 η πλευρά του ισοπλεύρου και
η πλευρά του ισοπλεύρου και 
 είναι ορθογώνιο και ισοσκελές άρα
είναι ορθογώνιο και ισοσκελές άρα  . Από το εγγράψιμο
. Από το εγγράψιμο  έχουμε ότι
έχουμε ότι 
 .Το
.Το  είναι ισοσκελές ,έστω
είναι ισοσκελές ,έστω 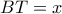 . Είναι
. Είναι 
 .Με νόμο συνημιτόνων στο
.Με νόμο συνημιτόνων στο  είναι
είναι 
 στην
στην  παίρνουμε εύκολα ότι
παίρνουμε εύκολα ότι 

Καλησπέρα. Άλλη μια λύση στο πνεύμα των προηγουμένων... Φέρω τηνΜιχάλης Νάννος έγραψε: ↑Τετ Ιουν 26, 2019 4:07 pmshape.pngΣτο εσωτερικό ισοπλεύρου τριγώνου, παίρνουμε σημείο
και φέρουμε τις προβολές
στις πλευρές
αντίστοιχα.
Ανκαι
, να βρείτε το μήκος του τμήματος

 κάθετη στην
κάθετη στην  και την
και την  κάθετη στην
κάθετη στην  .
. είναι εγγράψιμο.
είναι εγγράψιμο. και
και  .
. έχουμε :
έχουμε :  , οπότε
, οπότε  .
. .
.  έχουμε
έχουμε  και επειδή
και επειδή 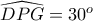
 επομένως
επομένως  .
. προκύπτει
προκύπτει  .
. αλλά και
αλλά και 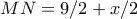 . Οπότε
. Οπότε  και
και  . Φιλικά , Γιώργος.
. Φιλικά , Γιώργος.Μιχάλης Νάννος έγραψε: ↑Τετ Ιουν 26, 2019 4:07 pmshape.pngΣτο εσωτερικό ισοπλεύρου τριγώνου, παίρνουμε σημείο
και φέρουμε τις προβολές
στις πλευρές
αντίστοιχα.
Ανκαι
, να βρείτε το μήκος του τμήματος



Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 20 επισκέπτες