Ωραία! Και γω κινήθηκα παρόμοια. Έστω

Τότε μπορούμε να γράψουμε
 όπου
όπου  .
. Από τη μονοτονία της
 προκύπτει ο μοναδικός μηδενισμός της
προκύπτει ο μοναδικός μηδενισμός της  στο σημείο όπου
στο σημείο όπου  , δηλαδή στο
, δηλαδή στο  .
.Το ωραίο είναι ότι το ελάχιστο (παρόλο που είναι περίεργο νούμερο), βγαίνει χωρίς καθόλου πράξεις!
Θα μπορούσε άνετα να είχε ζητηθεί στο διαγώνισμα.

 και την
και την  προκύπτει η
προκύπτει η  .
.
 στο σημείο όπου
στο σημείο όπου 


 η οποία είναι παραγωγίσιμη με παράγωγο
η οποία είναι παραγωγίσιμη με παράγωγο  με την ισότητα να ισχύει μόνο για
με την ισότητα να ισχύει μόνο για  (λόγω του ερωτήματος Δ3i). Άρα η συνάρτηση
(λόγω του ερωτήματος Δ3i). Άρα η συνάρτηση  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  . Η προς απόδειξη ανισότητα γράφεται:
. Η προς απόδειξη ανισότητα γράφεται: 
 .
. . Δεν βλέπω πουθενά το ρόλο του
. Δεν βλέπω πουθενά το ρόλο του 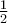 .
. ![\left [ \lambda ,\lambda +1 \right ] \left [ \lambda ,\lambda +1 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/b46597a24ef4ea91725555bfca101b2e.png) έχουμε ότι
έχουμε ότι 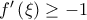 .
. ώστε να ισχύει
ώστε να ισχύει  .
. με
με  η οποία είναι γνησίως αύξουσα.
η οποία είναι γνησίως αύξουσα. ισχύει
ισχύει

 για κάθε τιμή του λ.
για κάθε τιμή του λ. αρα
αρα  ή
ή  και να πω αδυνατο αφου
και να πω αδυνατο αφου 
 έχουμε
έχουμε  η
η 
 ;
; για τα οποία είναι
για τα οποία είναι  ή
ή  .
. κλπ -- σημείο καμπής, οπότε η εφαπτομένη εκεί διαπερνά την καμπύλη και δεν μπορεί να είναι παράλληλη προς οποιαδήποτε χορδή της.
κλπ -- σημείο καμπής, οπότε η εφαπτομένη εκεί διαπερνά την καμπύλη και δεν μπορεί να είναι παράλληλη προς οποιαδήποτε χορδή της. είναι συνεχείς», θα ήταν πλήρης η αιτιολόγηση να πούμε «Λάθος διότι γνωρίζουμε ότι υπάρχουν συναρτήσεις η οποίες δεν είναι συνεχείς»; Νομίζω πως όχι διότι είναι σαν να λέμε «Λάθος διότι γνωρίζουμε ότι είναι λάθος».
είναι συνεχείς», θα ήταν πλήρης η αιτιολόγηση να πούμε «Λάθος διότι γνωρίζουμε ότι υπάρχουν συναρτήσεις η οποίες δεν είναι συνεχείς»; Νομίζω πως όχι διότι είναι σαν να λέμε «Λάθος διότι γνωρίζουμε ότι είναι λάθος». 





 για
για  ,
,  για
για  , ξεκάθαρες από την
, ξεκάθαρες από την  .
. αφού έχει σύνολο τιμών το
αφού έχει σύνολο τιμών το  και είναι γνησίως αύξουσα θα έχει μοναδική ρίζα .
και είναι γνησίως αύξουσα θα έχει μοναδική ρίζα . , αφού
, αφού  , αλλά ούτε και στο
, αλλά ούτε και στο  , αφού
, αφού , άρα υποχρεωτικά είναι αρνητική .
, άρα υποχρεωτικά είναι αρνητική .