 και
και  τα αντιδιαμετρικά των κορυφών στον περίκυκλο.Έστω
τα αντιδιαμετρικά των κορυφών στον περίκυκλο.Έστω  τα μέσα των τόξων
τα μέσα των τόξων  και
και 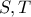 οι τομές της ευθείας που ενώνει το περίκεντρο με το έκκεντρο του τριγώνου,με τις
οι τομές της ευθείας που ενώνει το περίκεντρο με το έκκεντρο του τριγώνου,με τις  .Αν
.Αν  η εφαπτομένη στον
η εφαπτομένη στον  στο
στο  και
και  η τομή της με τον
η τομή της με τον  νδο.
νδο.  συντρέχουν.
συντρέχουν.Συντονιστές: vittasko, silouan, rek2
 και
και  τα αντιδιαμετρικά των κορυφών στον περίκυκλο.Έστω
τα αντιδιαμετρικά των κορυφών στον περίκυκλο.Έστω  τα μέσα των τόξων
τα μέσα των τόξων  και
και 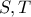 οι τομές της ευθείας που ενώνει το περίκεντρο με το έκκεντρο του τριγώνου,με τις
οι τομές της ευθείας που ενώνει το περίκεντρο με το έκκεντρο του τριγώνου,με τις  .Αν
.Αν  η εφαπτομένη στον
η εφαπτομένη στον  στο
στο  και
και  η τομή της με τον
η τομή της με τον  νδο.
νδο.  συντρέχουν.
συντρέχουν. , όπου
, όπου  είναι το έγκεντρο και το περίκεντρο αντιστοίχως, του δοσμένου τριγώνου
είναι το έγκεντρο και το περίκεντρο αντιστοίχως, του δοσμένου τριγώνου  .
. Αποδεικνύεται
Αποδεικνύεται  η απόδειξη αφήνεται στον αναγνώστη, ως άσκηση στα αρμονικά συζυγή
η απόδειξη αφήνεται στον αναγνώστη, ως άσκηση στα αρμονικά συζυγή  ότι ισχύει
ότι ισχύει  και επομένως, έχουμε ότι η ευθεία
και επομένως, έχουμε ότι η ευθεία  εφάπτεται στον περίκυκλο του τριγώνου
εφάπτεται στον περίκυκλο του τριγώνου  και άρα,
και άρα,  .
. , το σημείο επαφής του έγκυκλου
, το σημείο επαφής του έγκυκλου  του
του  στην πλευρά
στην πλευρά  και έστω το σημείο
και έστω το σημείο 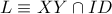 .
. , είναι συνευθειακά
, είναι συνευθειακά  γνωστό αποτέλεσμα που αποδεικνύεται εύκολα
γνωστό αποτέλεσμα που αποδεικνύεται εύκολα  .
. και
και  .
. όχι δύσκολα και θα ακολουθήσει το σχετικό Λήμμα
όχι δύσκολα και θα ακολουθήσει το σχετικό Λήμμα ότι ισχύει
ότι ισχύει  .
.
 Παρατηρούμε τώρα, ότι οι δια των κορυφών
Παρατηρούμε τώρα, ότι οι δια των κορυφών 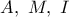 του τριγώνου
του τριγώνου  κάθετες ευθείες, επί των ευθειών των πλευρών
κάθετες ευθείες, επί των ευθειών των πλευρών  αντιστοίχως, του τριγώνου
αντιστοίχως, του τριγώνου  , συντρέχουν στο σημείο
, συντρέχουν στο σημείο 

 και
και  και
και 
 και άρα, τα τρίγωνα
και άρα, τα τρίγωνα  είναι ορθολογικά.
είναι ορθολογικά. , ως οι δια των κορυφών
, ως οι δια των κορυφών  κάθετες ευθείες επί των ευθειών των πλευρών
κάθετες ευθείες επί των ευθειών των πλευρών  αντιστοίχως, του τριγώνου
αντιστοίχως, του τριγώνου 

 και
και  λόγω
λόγω  και
και 
 , τέμνονται στο ίδιο σημείο έστω
, τέμνονται στο ίδιο σημείο έστω  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. αργότερα, αν δεν απαντηθεί.
αργότερα, αν δεν απαντηθεί.ΛΗΜΜΑ. - Δίνεται τρίγωνο
 με περίκυκλο
με περίκυκλο  , έγκυκλο
, έγκυκλο  και ας είναι
και ας είναι  , τα σημεία τομής του
, τα σημεία τομής του  από τις ευθείες
από τις ευθείες  αντιστοίχως, με
αντιστοίχως, με  το κέντρο του
το κέντρο του  . Έστω τα σημεία
. Έστω τα σημεία  και
και  και
και  , όπου
, όπου  είναι το κέντρο του
είναι το κέντρο του  και
και  , το σημείο επαφής του
, το σημείο επαφής του  στην
στην  και
και  , τα αντιδιαμετρικά σημεία των
, τα αντιδιαμετρικά σημεία των  , αντιστοίχως. Αποδείξτε ότι
, αντιστοίχως. Αποδείξτε ότι  .
. Η ευθεία
Η ευθεία  ταυτίζεται με την μεσοκάθετη ευθεία του
ταυτίζεται με την μεσοκάθετη ευθεία του  ( γνωστό αποτέλεσμα που αποδεικνύεται εύκολα ) και έστω το σημείο
( γνωστό αποτέλεσμα που αποδεικνύεται εύκολα ) και έστω το σημείο  .
. είναι συμμετρικές ως προς την ευθεία
είναι συμμετρικές ως προς την ευθεία  .
. είναι επίσης και οι ευθείες
είναι επίσης και οι ευθείες  , όπου
, όπου 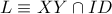 και επομένως, ισχύει
και επομένως, ισχύει 

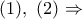

 και άρα, τα σημεία
και άρα, τα σημεία  είναι συνευθειακά και οι ευθείες
είναι συνευθειακά και οι ευθείες  είναι συμμετρικές ως προς την
είναι συμμετρικές ως προς την  .
.
 Προκύπτει έτσι, ότι και οι ευθείες
Προκύπτει έτσι, ότι και οι ευθείες  είναι επίσης συμμετρικές ως προς την
είναι επίσης συμμετρικές ως προς την  και άρα, έχουμε
και άρα, έχουμε 
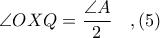 λόγω του εγγραψίμου τετραπλεύρου
λόγω του εγγραψίμου τετραπλεύρου  , όπου
, όπου  .
.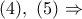

 έχουμε ότι το τετράπλευρο
έχουμε ότι το τετράπλευρο  , όπου
, όπου  είναι εγγράψιμο και άρα, προκύπτει
είναι εγγράψιμο και άρα, προκύπτει  , λόγω
, λόγω  και άρα, έχουμε
και άρα, έχουμε 
 και
και  , συμπεραίνεται ότι
, συμπεραίνεται ότι  και το Λήμμα έχει αποδειχθεί.
και το Λήμμα έχει αποδειχθεί. .
. και
και  τέμνονται στο
τέμνονται στο  . Προφανώς το
. Προφανώς το  προκύπτει να είναι το αντιδιαμετρικό του
προκύπτει να είναι το αντιδιαμετρικό του  στο τρίγωνο
στο τρίγωνο  .
. , τα
, τα 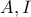 είναι συζυγή, όπως και τα τρίγωνα
είναι συζυγή, όπως και τα τρίγωνα  και
και  , άρα τα
, άρα τα  και
και  είναι συζυγή.
είναι συζυγή. που το ορίζουμε εκ νέου ως την τομή της
που το ορίζουμε εκ νέου ως την τομή της  και του περιγεγραμμένου κύκλου του
και του περιγεγραμμένου κύκλου του  , έχει συζυγές το
, έχει συζυγές το 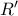 , όπου είναι η τομή της
, όπου είναι η τομή της  , δηλαδή της
, δηλαδή της 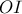 , με την
, με την  .
. το σημείο τομής της
το σημείο τομής της  και
και  .
. είναι συνευθειακά.
είναι συνευθειακά. το σημείο τομής της
το σημείο τομής της  και
και  .
. αυτό βρίσκεται πάνω στην
αυτό βρίσκεται πάνω στην 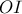 .
. συνιστά την πολική του
συνιστά την πολική του  στον περιγεγραμμένο κύκλο του
στον περιγεγραμμένο κύκλο του  .
.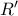 ανήκει στην πολική του
ανήκει στην πολική του  .
.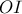 τέμνει τον περιγεγραμμένο στα
τέμνει τον περιγεγραμμένο στα  .
. είναι μέσο του
είναι μέσο του 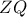 , αρκεί από
, αρκεί από  :
:  .
. να είναι εγγράψιμο.
να είναι εγγράψιμο.
 είναι εφαπτομένη στο
είναι εφαπτομένη στο  (η αρχή της λύσης του κύριου Βήττα)
(η αρχή της λύσης του κύριου Βήττα) τέμνει τις
τέμνει τις  και
και  στα
στα 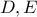 .
.
 είναι ρόμβος.
είναι ρόμβος. και
και  , άρα
, άρα  και από θεώρημα διχοτόμων στο
και από θεώρημα διχοτόμων στο  , έχουμε πως
, έχουμε πως  και ως γνωστό έπεται ότι η
και ως γνωστό έπεται ότι η  είναι εφαπτομένη στο
είναι εφαπτομένη στο  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 16 επισκέπτες