Υ.γ: Αν μπορέσω να βρω τα θέματα θα προσπαθήσω να τα ανεβάσω !
EGMO 2019
Συντονιστής: spyros
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
EGMO 2019
Σήμερα ξεκινάει η EGMO 2019 στην οποία η Ελλάδα συμμετέχει για δεύτερη φορά. Να ευχηθούμε καλή επιτυχία στην Ελληνική ομάδα ( Ειρηνούλα θέλω χρυσό  ) καθώς και στην Κυπριακή στην οποία leader είναι ο "δικός μας" Δημήτρης Χριστοφίδης!!!
) καθώς και στην Κυπριακή στην οποία leader είναι ο "δικός μας" Δημήτρης Χριστοφίδης!!!
Υ.γ: Αν μπορέσω να βρω τα θέματα θα προσπαθήσω να τα ανεβάσω !
Υ.γ: Αν μπορέσω να βρω τα θέματα θα προσπαθήσω να τα ανεβάσω !
Λέξεις Κλειδιά:
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: EGMO 2019
Ξεκινώ με τα θέματα της 1ης μέρας! Ευχαριστώ τον Αρχηγό της Ελληνικής Αποστολής Αχιλλέα Συνεφακόπουλο που μου τα έστειλε.
Εύχομαι καλή αρχή στην Ελληνική και Κυπριακή Αποστολή!
Πρόβλημα 1
Να βρεθούν όλες οι τριάδες πραγματικών αριθμών τέτοιων ώστε
πραγματικών αριθμών τέτοιων ώστε  και
και 
Πρόβλημα 2
Έστω ένας θετικός ακέραιος. Τοποθετούνται ντόμινο σε ένα
ένας θετικός ακέραιος. Τοποθετούνται ντόμινο σε ένα  πίνακα με τέτοιο τρόπο ώστε κάθε κελί του πίνακα να είναι γειτονικό με ακριβώς ένα κελί το οποίο να καλύπτεται από ένα ντόμινο. Για κάθε
πίνακα με τέτοιο τρόπο ώστε κάθε κελί του πίνακα να είναι γειτονικό με ακριβώς ένα κελί το οποίο να καλύπτεται από ένα ντόμινο. Για κάθε  , να προσδιοριστεί το μέγιστο πλήθος των ντόμινο που μπορούν να τοποθετηθούν με αυτόν τον τρόπο.
, να προσδιοριστεί το μέγιστο πλήθος των ντόμινο που μπορούν να τοποθετηθούν με αυτόν τον τρόπο.
(Ένα ντόμινο είναι ένα πλακίδιο διαστάσεων ή
ή  . Τα ντόμινο τοποθετούνται στον πίνακα με τέτοιο τρόπο ώστε κάθε ντόμινο να καλύπτει ακριβώς δύο κελιά του πίνακα, και τα ντόμινο να μην αλληλοεπικαλύπτονται. Δύο κελιά ονομάζονται γειτονικά εάν είναι διαφορετικά και έχουν μία κοινή πλευρά).
. Τα ντόμινο τοποθετούνται στον πίνακα με τέτοιο τρόπο ώστε κάθε ντόμινο να καλύπτει ακριβώς δύο κελιά του πίνακα, και τα ντόμινο να μην αλληλοεπικαλύπτονται. Δύο κελιά ονομάζονται γειτονικά εάν είναι διαφορετικά και έχουν μία κοινή πλευρά).
Πρόβλημα 3
Έστω τρίγωνο τέτοιο ώστε
τέτοιο ώστε  , και έστω
, και έστω  το έγκεντρό του. Έστω
το έγκεντρό του. Έστω  σημείο στο τμήμα
σημείο στο τμήμα  τέτοιο ώστε
τέτοιο ώστε  . Έστω
. Έστω  ο κύκλος ο οποίος εφάπτεται της
ο κύκλος ο οποίος εφάπτεται της  στο
στο  και διέρχεται από το
και διέρχεται από το  Έστω
Έστω  το δεύτερο σημείο τομής του
το δεύτερο σημείο τομής του  με τον περιγεγγραμμένο κύκλο του
με τον περιγεγγραμμένο κύκλο του  Να αποδειχθεί ότι οι διχοτόμοι των γωνιών
Να αποδειχθεί ότι οι διχοτόμοι των γωνιών  και
και  τέμνονται σε σημείο της ευθείας
τέμνονται σε σημείο της ευθείας 
Αλέξανδρος
Εύχομαι καλή αρχή στην Ελληνική και Κυπριακή Αποστολή!
Πρόβλημα 1
Να βρεθούν όλες οι τριάδες
 πραγματικών αριθμών τέτοιων ώστε
πραγματικών αριθμών τέτοιων ώστε  και
και 
Πρόβλημα 2
Έστω
 ένας θετικός ακέραιος. Τοποθετούνται ντόμινο σε ένα
ένας θετικός ακέραιος. Τοποθετούνται ντόμινο σε ένα  πίνακα με τέτοιο τρόπο ώστε κάθε κελί του πίνακα να είναι γειτονικό με ακριβώς ένα κελί το οποίο να καλύπτεται από ένα ντόμινο. Για κάθε
πίνακα με τέτοιο τρόπο ώστε κάθε κελί του πίνακα να είναι γειτονικό με ακριβώς ένα κελί το οποίο να καλύπτεται από ένα ντόμινο. Για κάθε  , να προσδιοριστεί το μέγιστο πλήθος των ντόμινο που μπορούν να τοποθετηθούν με αυτόν τον τρόπο.
, να προσδιοριστεί το μέγιστο πλήθος των ντόμινο που μπορούν να τοποθετηθούν με αυτόν τον τρόπο.(Ένα ντόμινο είναι ένα πλακίδιο διαστάσεων
 ή
ή  . Τα ντόμινο τοποθετούνται στον πίνακα με τέτοιο τρόπο ώστε κάθε ντόμινο να καλύπτει ακριβώς δύο κελιά του πίνακα, και τα ντόμινο να μην αλληλοεπικαλύπτονται. Δύο κελιά ονομάζονται γειτονικά εάν είναι διαφορετικά και έχουν μία κοινή πλευρά).
. Τα ντόμινο τοποθετούνται στον πίνακα με τέτοιο τρόπο ώστε κάθε ντόμινο να καλύπτει ακριβώς δύο κελιά του πίνακα, και τα ντόμινο να μην αλληλοεπικαλύπτονται. Δύο κελιά ονομάζονται γειτονικά εάν είναι διαφορετικά και έχουν μία κοινή πλευρά).Πρόβλημα 3
Έστω τρίγωνο
 τέτοιο ώστε
τέτοιο ώστε  , και έστω
, και έστω  το έγκεντρό του. Έστω
το έγκεντρό του. Έστω  σημείο στο τμήμα
σημείο στο τμήμα  τέτοιο ώστε
τέτοιο ώστε  . Έστω
. Έστω  ο κύκλος ο οποίος εφάπτεται της
ο κύκλος ο οποίος εφάπτεται της  στο
στο  και διέρχεται από το
και διέρχεται από το  Έστω
Έστω  το δεύτερο σημείο τομής του
το δεύτερο σημείο τομής του  με τον περιγεγγραμμένο κύκλο του
με τον περιγεγγραμμένο κύκλο του  Να αποδειχθεί ότι οι διχοτόμοι των γωνιών
Να αποδειχθεί ότι οι διχοτόμοι των γωνιών  και
και  τέμνονται σε σημείο της ευθείας
τέμνονται σε σημείο της ευθείας 
Αλέξανδρος
Αλέξανδρος Συγκελάκης
Re: EGMO 2019
Πρόβλημα 1. Να βρεθούν όλες οι τριάδες  πραγματικών αριθμών τέτοιων ώστε
πραγματικών αριθμών τέτοιων ώστε  και
και

********************************************************************
Λύση: Έχουμε

κι έτσι

Ομοίως, έχουμε

Αν , τότε παίρνουμε
, τότε παίρνουμε  και
και  , που δίνουν
, που δίνουν  , ή
, ή  .
.
Ομοίως, εάν , τότε
, τότε  , ή
, ή  , ενώ αν
, ενώ αν  , τότε
, τότε  , ή
, ή 
Έτσι, ας υποθέσουμε ότι . Τότε
. Τότε
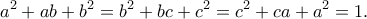
Προσθέτοντας τες, παίρνουμε

και χρησιμοποιώντας τη σχέση , παίρνουμε
, παίρνουμε

Συνεπώς,

κι έτσι , οπότε
, οπότε  .
.
Συνεπώς, οι λύσεις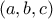 είναι
είναι  ,
, 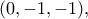
 ,
, 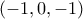 ,
,  ,
,  ,
,  ,
, 
Φιλικά,
Αχιλλέας
 πραγματικών αριθμών τέτοιων ώστε
πραγματικών αριθμών τέτοιων ώστε  και
και
********************************************************************
Λύση: Έχουμε

κι έτσι

Ομοίως, έχουμε

Αν
 , τότε παίρνουμε
, τότε παίρνουμε  και
και  , που δίνουν
, που δίνουν  , ή
, ή  .
. Ομοίως, εάν
 , τότε
, τότε  , ή
, ή  , ενώ αν
, ενώ αν  , τότε
, τότε  , ή
, ή 
Έτσι, ας υποθέσουμε ότι
 . Τότε
. Τότε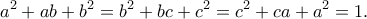
Προσθέτοντας τες, παίρνουμε

και χρησιμοποιώντας τη σχέση
 , παίρνουμε
, παίρνουμε
Συνεπώς,

κι έτσι
 , οπότε
, οπότε  .
.Συνεπώς, οι λύσεις
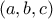 είναι
είναι  ,
, 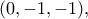
 ,
, 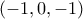 ,
,  ,
,  ,
,  ,
, 
Φιλικά,
Αχιλλέας
Re: EGMO 2019
Πρόβλημα 3. Έστω τρίγωνο  τέτοιο ώστε
τέτοιο ώστε  , και έστω
, και έστω  το έγκεντρό του. Έστω
το έγκεντρό του. Έστω  σημείο στο τμήμα
σημείο στο τμήμα  τέτοιο ώστε
τέτοιο ώστε  . Έστω
. Έστω  ο κύκλος ο οποίος εφάπτεται της
ο κύκλος ο οποίος εφάπτεται της  στο
στο  και διέρχεται από το
και διέρχεται από το  Έστω
Έστω  το δεύτερο σημείο τομής του
το δεύτερο σημείο τομής του  με τον περιγεγγραμμένο κύκλο του
με τον περιγεγγραμμένο κύκλο του  Να αποδειχθεί ότι οι διχοτόμοι των γωνιών
Να αποδειχθεί ότι οι διχοτόμοι των γωνιών  και
και  τέμνονται σε σημείο της ευθείας
τέμνονται σε σημείο της ευθείας 
********************************************************************
Λύση: Παρατηρούμε ότι
Έστω ότι οι και
και  τέμνονται στο
τέμνονται στο  . Τότε
. Τότε 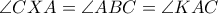 .
.
Επίσης, έχουμε , αφού ο
, αφού ο  εφάπτεται στην
εφάπτεται στην  στο
στο  . Επομένως,
. Επομένως,

(η απόλυτη τιμή εξαρτάται από το αν ή όχι) που σημαίνει ότι το τετράπλευρο
ή όχι) που σημαίνει ότι το τετράπλευρο  είναι εγγράψιμο, δηλ. το
είναι εγγράψιμο, δηλ. το  ανήκει στον
ανήκει στον 
Έστω ότι η ευθεία τέμνει την
τέμνει την  στο
στο  . (Αν
. (Αν  , τότε η
, τότε η  "εκφυλίζεται" στην εφαπτόμενη στον
"εκφυλίζεται" στην εφαπτόμενη στον  στο
στο  )
)
Παρατηρούμε ότι το τετράπλευρο είναι εγγράψιμο, αφού
είναι εγγράψιμο, αφού

Έχουμε και
και  . Έτσι
. Έτσι

Αυτό σημαίνει ότι η είναι διχοτόμος της
είναι διχοτόμος της  Έπειτα, έστω
Έπειτα, έστω  το σημείο τομής των
το σημείο τομής των  και
και  Τότε
Τότε

κι έτσι η παραπληρωματική της γωνία ισούται με

κι άρα τα βρίσκονται στον
βρίσκονται στον  Έπειτα, έχουμε
Έπειτα, έχουμε
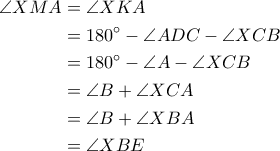
κι άρα τα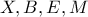 είναι ομοκυκλικά. Έτσι,
είναι ομοκυκλικά. Έτσι,

Άρα η είναι διχοτόμος της
είναι διχοτόμος της  , όπως θέλαμε!
, όπως θέλαμε!
Φιλικά,
Αχιλλέας
 τέτοιο ώστε
τέτοιο ώστε  , και έστω
, και έστω  το έγκεντρό του. Έστω
το έγκεντρό του. Έστω  σημείο στο τμήμα
σημείο στο τμήμα  τέτοιο ώστε
τέτοιο ώστε  . Έστω
. Έστω  ο κύκλος ο οποίος εφάπτεται της
ο κύκλος ο οποίος εφάπτεται της  στο
στο  και διέρχεται από το
και διέρχεται από το  Έστω
Έστω  το δεύτερο σημείο τομής του
το δεύτερο σημείο τομής του  με τον περιγεγγραμμένο κύκλο του
με τον περιγεγγραμμένο κύκλο του  Να αποδειχθεί ότι οι διχοτόμοι των γωνιών
Να αποδειχθεί ότι οι διχοτόμοι των γωνιών  και
και  τέμνονται σε σημείο της ευθείας
τέμνονται σε σημείο της ευθείας 
********************************************************************
Λύση: Παρατηρούμε ότι

Έστω ότι οι
 και
και  τέμνονται στο
τέμνονται στο  . Τότε
. Τότε 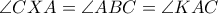 .
. Επίσης, έχουμε
 , αφού ο
, αφού ο  εφάπτεται στην
εφάπτεται στην  στο
στο  . Επομένως,
. Επομένως, 
(η απόλυτη τιμή εξαρτάται από το αν
 ή όχι) που σημαίνει ότι το τετράπλευρο
ή όχι) που σημαίνει ότι το τετράπλευρο  είναι εγγράψιμο, δηλ. το
είναι εγγράψιμο, δηλ. το  ανήκει στον
ανήκει στον 
Έστω ότι η ευθεία
 τέμνει την
τέμνει την  στο
στο  . (Αν
. (Αν  , τότε η
, τότε η  "εκφυλίζεται" στην εφαπτόμενη στον
"εκφυλίζεται" στην εφαπτόμενη στον  στο
στο  )
) Παρατηρούμε ότι το τετράπλευρο
 είναι εγγράψιμο, αφού
είναι εγγράψιμο, αφού
Έχουμε
 και
και  . Έτσι
. Έτσι
Αυτό σημαίνει ότι η
 είναι διχοτόμος της
είναι διχοτόμος της  Έπειτα, έστω
Έπειτα, έστω  το σημείο τομής των
το σημείο τομής των  και
και  Τότε
Τότε
κι έτσι η παραπληρωματική της γωνία ισούται με

κι άρα τα
 βρίσκονται στον
βρίσκονται στον  Έπειτα, έχουμε
Έπειτα, έχουμε
κι άρα τα
 είναι ομοκυκλικά. Έτσι,
είναι ομοκυκλικά. Έτσι,
Άρα η
 είναι διχοτόμος της
είναι διχοτόμος της  , όπως θέλαμε!
, όπως θέλαμε!Φιλικά,
Αχιλλέας
- Συνημμένα
-
- egmo_3_mathematica.png (44.59 KiB) Προβλήθηκε 2387 φορές
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: EGMO 2019
Βάζω μια λύση για τη 2. (Συμπλήρωσα τώρα και την κατασκευή.) Η λύση μου είναι διαφορετική από την επίσημη (η οποία δεν έχει ακόμη αναρτηθεί).
Έστω ότι έχουμε γωνιακά ντόμινο,
γωνιακά ντόμινο,  πλευρικά,
πλευρικά,  για τα οποία το ένα κελί είναι πλευρικό και το άλλο όχι, και
για τα οποία το ένα κελί είναι πλευρικό και το άλλο όχι, και  τα οποία δεν έχουν κανένα κελί στο πλευρό.
τα οποία δεν έχουν κανένα κελί στο πλευρό.
Όλα αυτά καλύπτουν συνολικά κελιά. Επίσης, κοιτάζοντας τα κελιά στον περίγυρο, βλέπουμε ότι
κελιά. Επίσης, κοιτάζοντας τα κελιά στον περίγυρο, βλέπουμε ότι  .
.
Άρα:

αφού . Άρα χρησιμοποιήσαμε το πολύ
. Άρα χρησιμοποιήσαμε το πολύ  ντόμινο.
ντόμινο.
Η κατασκευή για είναι απλή. Αν έχουμε την κατασκευή για
είναι απλή. Αν έχουμε την κατασκευή για  θα δείξουμε πως παίρνουμε την κατασκευή για
θα δείξουμε πως παίρνουμε την κατασκευή για  . Ξεκινάμε από τον
. Ξεκινάμε από τον  πίνακα και στον περίγυρο εναλλάξ είτε τοποθετούμε ντόμινο σε δύο κελιά είτε τα αφήνουμε κενά όπως στο πιο κάτω σχήμα. Όλα τα κελιά στον περίγυρο έχουν την ζητούμενη ιδιότητα. Μας μένει ένας
πίνακα και στον περίγυρο εναλλάξ είτε τοποθετούμε ντόμινο σε δύο κελιά είτε τα αφήνουμε κενά όπως στο πιο κάτω σχήμα. Όλα τα κελιά στον περίγυρο έχουν την ζητούμενη ιδιότητα. Μας μένει ένας 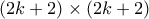 πίνακας στον περίγυρο του οποίου δεν θα τοποθετήσουμε κανένα ντόμινο. Στο σχήμα έχουμε σημειώσει τα κελιά τα οποία ακόμη δεν έχουν τη ζητούμενη ιδιότητα. Αυτά είναι ακριβώς τα κελιά τα οποία δεν είναι γωνιακά και είναι γειτονικά σε κελιά του αρχικού περίγυρου στα οποία δεν τοποθετήθηκε ντόμινο. (Με τα γωνιακά κελιά είμαστε πάντα εντάξει.) Μπορούμε τώρα να δούμε ότι μπορούμε να τοποθετήσουμε ντόμινο εναλλάξ στον περίγυρο του εσωτερικού
πίνακας στον περίγυρο του οποίου δεν θα τοποθετήσουμε κανένα ντόμινο. Στο σχήμα έχουμε σημειώσει τα κελιά τα οποία ακόμη δεν έχουν τη ζητούμενη ιδιότητα. Αυτά είναι ακριβώς τα κελιά τα οποία δεν είναι γωνιακά και είναι γειτονικά σε κελιά του αρχικού περίγυρου στα οποία δεν τοποθετήθηκε ντόμινο. (Με τα γωνιακά κελιά είμαστε πάντα εντάξει.) Μπορούμε τώρα να δούμε ότι μπορούμε να τοποθετήσουμε ντόμινο εναλλάξ στον περίγυρο του εσωτερικού  πίνακα ώστε να καλύπτουν ακριβώς τα ακάλυπτα κελιά του περίγυρου του
πίνακα ώστε να καλύπτουν ακριβώς τα ακάλυπτα κελιά του περίγυρου του 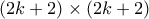 πίνακα. Η κάλυψη του
πίνακα. Η κάλυψη του  πίνακα συμπληρώνεται επαγωγικά.
πίνακα συμπληρώνεται επαγωγικά.
Σημείωση: Οι περιπτώσεις περιττός και
περιττός και  άρτιος έχουν λίγο διαφορετικό σχήμα αλλά τίποτα το ουσιαστικά διαφορετικό.
άρτιος έχουν λίγο διαφορετικό σχήμα αλλά τίποτα το ουσιαστικά διαφορετικό.
![\begin{tikzpicture}[scale=0.8,line cap=round,line join=round,>=triangle 45,x=1.0cm,y=1.0cm]
\clip(-0.98,-0.76) rectangle (10.96,10.66);
\fill[line width=2.pt,fill=black,fill opacity=1.0] (0.,8.) -- (1.,8.) -- (1.,10.) -- (0.,10.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (0.,6.) -- (1.,6.) -- (1.,4.) -- (0.,4.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (0.,2.) -- (0.,0.) -- (1.,0.) -- (1.,2.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (3.,1.) -- (3.,0.) -- (5.,0.) -- (5.,1.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (7.,1.) -- (7.,0.) -- (9.,0.) -- (9.,1.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (9.,2.) -- (10.,2.) -- (10.,4.) -- (9.,4.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (9.,6.) -- (10.,6.) -- (10.,8.) -- (9.,8.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (9.,9.) -- (9.,10.) -- (7.,10.) -- (7.,9.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (5.,9.) -- (5.,10.) -- (3.,10.) -- (3.,9.) -- cycle;
\draw [line width=2.pt] (0.,0.)-- (0.,10.);
\draw [line width=2.pt] (0.,10.)-- (10.,10.);
\draw [line width=2.pt] (10.,10.)-- (10.,0.);
\draw [line width=2.pt] (10.,0.)-- (0.,0.);
\draw [line width=2.pt] (1.,1.)-- (1.,9.);
\draw [line width=2.pt] (1.,9.)-- (9.,9.);
\draw [line width=2.pt] (9.,9.)-- (9.,1.);
\draw [line width=2.pt] (9.,1.)-- (1.,1.);
\draw [line width=2.pt] (0.,8.)-- (1.,8.);
\draw [line width=2.pt] (1.,8.)-- (1.,10.);
\draw [line width=2.pt] (1.,10.)-- (0.,10.);
\draw [line width=2.pt] (0.,10.)-- (0.,8.);
\draw [line width=2.pt] (0.,6.)-- (1.,6.);
\draw [line width=2.pt] (1.,6.)-- (1.,4.);
\draw [line width=2.pt] (1.,4.)-- (0.,4.);
\draw [line width=2.pt] (0.,4.)-- (0.,6.);
\draw [line width=2.pt] (0.,2.)-- (0.,0.);
\draw [line width=2.pt] (0.,0.)-- (1.,0.);
\draw [line width=2.pt] (1.,0.)-- (1.,2.);
\draw [line width=2.pt] (1.,2.)-- (0.,2.);
\draw [line width=2.pt] (3.,1.)-- (3.,0.);
\draw [line width=2.pt] (3.,0.)-- (5.,0.);
\draw [line width=2.pt] (5.,0.)-- (5.,1.);
\draw [line width=2.pt] (5.,1.)-- (3.,1.);
\draw [line width=2.pt] (7.,1.)-- (7.,0.);
\draw [line width=2.pt] (7.,0.)-- (9.,0.);
\draw [line width=2.pt] (9.,0.)-- (9.,1.);
\draw [line width=2.pt] (9.,1.)-- (7.,1.);
\draw [line width=2.pt] (9.,2.)-- (10.,2.);
\draw [line width=2.pt] (10.,2.)-- (10.,4.);
\draw [line width=2.pt] (10.,4.)-- (9.,4.);
\draw [line width=2.pt] (9.,4.)-- (9.,2.);
\draw [line width=2.pt] (9.,6.)-- (10.,6.);
\draw [line width=2.pt] (10.,6.)-- (10.,8.);
\draw [line width=2.pt] (10.,8.)-- (9.,8.);
\draw [line width=2.pt] (9.,8.)-- (9.,6.);
\draw [line width=2.pt] (9.,9.)-- (9.,10.);
\draw [line width=2.pt] (9.,10.)-- (7.,10.);
\draw [line width=2.pt] (7.,10.)-- (7.,9.);
\draw [line width=2.pt] (7.,9.)-- (9.,9.);
\draw [line width=2.pt] (5.,9.)-- (5.,10.);
\draw [line width=2.pt] (5.,10.)-- (3.,10.);
\draw [line width=2.pt] (3.,10.)-- (3.,9.);
\draw [line width=2.pt] (3.,9.)-- (5.,9.);
\draw [line width=2.pt] (2.,8.)-- (2.,2.);
\draw [line width=2.pt] (2.,8.)-- (8.,8.);
\draw [line width=2.pt] (8.,8.)-- (8.,2.);
\draw [line width=2.pt] (8.,2.)-- (2.,2.);
\draw [fill=black] (1.5,7.5) circle (2.0pt);
\draw [fill= black] (1.5,6.5) circle (2.0pt);
\draw [fill= black] (2.5,8.5) circle (2.0pt);
\draw [fill= black] (1.5,3.5) circle (2.0pt);
\draw [fill= black] (1.5,2.5) circle (2.0pt);
\draw [fill= black] (5.5,8.5) circle (2.0pt);
\draw [fill= black] (6.5,8.5) circle (2.0pt);
\draw [fill= black] (8.5,5.5) circle (2.0pt);
\draw [fill= black] (8.5,4.5) circle (2.0pt);
\draw [fill= black] (6.5,1.5) circle (2.0pt);
\draw [fill= black] (5.5,1.5) circle (2.0pt);
\draw [fill= black] (2.5,1.5) circle (2.0pt);
\end{tikzpicture}
\begin{tikzpicture}[scale=0.8,line cap=round,line join=round,>=triangle 45,x=1.0cm,y=1.0cm]
\clip(-0.98,-0.76) rectangle (10.96,10.66);
\fill[line width=2.pt,fill=black,fill opacity=1.0] (0.,8.) -- (1.,8.) -- (1.,10.) -- (0.,10.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (0.,6.) -- (1.,6.) -- (1.,4.) -- (0.,4.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (0.,2.) -- (0.,0.) -- (1.,0.) -- (1.,2.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (3.,1.) -- (3.,0.) -- (5.,0.) -- (5.,1.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (7.,1.) -- (7.,0.) -- (9.,0.) -- (9.,1.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (9.,2.) -- (10.,2.) -- (10.,4.) -- (9.,4.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (9.,6.) -- (10.,6.) -- (10.,8.) -- (9.,8.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (9.,9.) -- (9.,10.) -- (7.,10.) -- (7.,9.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (5.,9.) -- (5.,10.) -- (3.,10.) -- (3.,9.) -- cycle;
\draw [line width=2.pt] (0.,0.)-- (0.,10.);
\draw [line width=2.pt] (0.,10.)-- (10.,10.);
\draw [line width=2.pt] (10.,10.)-- (10.,0.);
\draw [line width=2.pt] (10.,0.)-- (0.,0.);
\draw [line width=2.pt] (1.,1.)-- (1.,9.);
\draw [line width=2.pt] (1.,9.)-- (9.,9.);
\draw [line width=2.pt] (9.,9.)-- (9.,1.);
\draw [line width=2.pt] (9.,1.)-- (1.,1.);
\draw [line width=2.pt] (0.,8.)-- (1.,8.);
\draw [line width=2.pt] (1.,8.)-- (1.,10.);
\draw [line width=2.pt] (1.,10.)-- (0.,10.);
\draw [line width=2.pt] (0.,10.)-- (0.,8.);
\draw [line width=2.pt] (0.,6.)-- (1.,6.);
\draw [line width=2.pt] (1.,6.)-- (1.,4.);
\draw [line width=2.pt] (1.,4.)-- (0.,4.);
\draw [line width=2.pt] (0.,4.)-- (0.,6.);
\draw [line width=2.pt] (0.,2.)-- (0.,0.);
\draw [line width=2.pt] (0.,0.)-- (1.,0.);
\draw [line width=2.pt] (1.,0.)-- (1.,2.);
\draw [line width=2.pt] (1.,2.)-- (0.,2.);
\draw [line width=2.pt] (3.,1.)-- (3.,0.);
\draw [line width=2.pt] (3.,0.)-- (5.,0.);
\draw [line width=2.pt] (5.,0.)-- (5.,1.);
\draw [line width=2.pt] (5.,1.)-- (3.,1.);
\draw [line width=2.pt] (7.,1.)-- (7.,0.);
\draw [line width=2.pt] (7.,0.)-- (9.,0.);
\draw [line width=2.pt] (9.,0.)-- (9.,1.);
\draw [line width=2.pt] (9.,1.)-- (7.,1.);
\draw [line width=2.pt] (9.,2.)-- (10.,2.);
\draw [line width=2.pt] (10.,2.)-- (10.,4.);
\draw [line width=2.pt] (10.,4.)-- (9.,4.);
\draw [line width=2.pt] (9.,4.)-- (9.,2.);
\draw [line width=2.pt] (9.,6.)-- (10.,6.);
\draw [line width=2.pt] (10.,6.)-- (10.,8.);
\draw [line width=2.pt] (10.,8.)-- (9.,8.);
\draw [line width=2.pt] (9.,8.)-- (9.,6.);
\draw [line width=2.pt] (9.,9.)-- (9.,10.);
\draw [line width=2.pt] (9.,10.)-- (7.,10.);
\draw [line width=2.pt] (7.,10.)-- (7.,9.);
\draw [line width=2.pt] (7.,9.)-- (9.,9.);
\draw [line width=2.pt] (5.,9.)-- (5.,10.);
\draw [line width=2.pt] (5.,10.)-- (3.,10.);
\draw [line width=2.pt] (3.,10.)-- (3.,9.);
\draw [line width=2.pt] (3.,9.)-- (5.,9.);
\draw [line width=2.pt] (2.,8.)-- (2.,2.);
\draw [line width=2.pt] (2.,8.)-- (8.,8.);
\draw [line width=2.pt] (8.,8.)-- (8.,2.);
\draw [line width=2.pt] (8.,2.)-- (2.,2.);
\draw [fill=black] (1.5,7.5) circle (2.0pt);
\draw [fill= black] (1.5,6.5) circle (2.0pt);
\draw [fill= black] (2.5,8.5) circle (2.0pt);
\draw [fill= black] (1.5,3.5) circle (2.0pt);
\draw [fill= black] (1.5,2.5) circle (2.0pt);
\draw [fill= black] (5.5,8.5) circle (2.0pt);
\draw [fill= black] (6.5,8.5) circle (2.0pt);
\draw [fill= black] (8.5,5.5) circle (2.0pt);
\draw [fill= black] (8.5,4.5) circle (2.0pt);
\draw [fill= black] (6.5,1.5) circle (2.0pt);
\draw [fill= black] (5.5,1.5) circle (2.0pt);
\draw [fill= black] (2.5,1.5) circle (2.0pt);
\end{tikzpicture}](/forum/ext/geomar/texintegr/latexrender/pictures/ba77d6b6db28f7cc72a2d7df6a37fab0.png)
Έστω ότι έχουμε
 γωνιακά ντόμινο,
γωνιακά ντόμινο,  πλευρικά,
πλευρικά,  για τα οποία το ένα κελί είναι πλευρικό και το άλλο όχι, και
για τα οποία το ένα κελί είναι πλευρικό και το άλλο όχι, και  τα οποία δεν έχουν κανένα κελί στο πλευρό.
τα οποία δεν έχουν κανένα κελί στο πλευρό.Όλα αυτά καλύπτουν συνολικά
 κελιά. Επίσης, κοιτάζοντας τα κελιά στον περίγυρο, βλέπουμε ότι
κελιά. Επίσης, κοιτάζοντας τα κελιά στον περίγυρο, βλέπουμε ότι  .
.Άρα:

αφού
 . Άρα χρησιμοποιήσαμε το πολύ
. Άρα χρησιμοποιήσαμε το πολύ  ντόμινο.
ντόμινο. Η κατασκευή για
 είναι απλή. Αν έχουμε την κατασκευή για
είναι απλή. Αν έχουμε την κατασκευή για  θα δείξουμε πως παίρνουμε την κατασκευή για
θα δείξουμε πως παίρνουμε την κατασκευή για  . Ξεκινάμε από τον
. Ξεκινάμε από τον  πίνακα και στον περίγυρο εναλλάξ είτε τοποθετούμε ντόμινο σε δύο κελιά είτε τα αφήνουμε κενά όπως στο πιο κάτω σχήμα. Όλα τα κελιά στον περίγυρο έχουν την ζητούμενη ιδιότητα. Μας μένει ένας
πίνακα και στον περίγυρο εναλλάξ είτε τοποθετούμε ντόμινο σε δύο κελιά είτε τα αφήνουμε κενά όπως στο πιο κάτω σχήμα. Όλα τα κελιά στον περίγυρο έχουν την ζητούμενη ιδιότητα. Μας μένει ένας 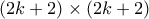 πίνακας στον περίγυρο του οποίου δεν θα τοποθετήσουμε κανένα ντόμινο. Στο σχήμα έχουμε σημειώσει τα κελιά τα οποία ακόμη δεν έχουν τη ζητούμενη ιδιότητα. Αυτά είναι ακριβώς τα κελιά τα οποία δεν είναι γωνιακά και είναι γειτονικά σε κελιά του αρχικού περίγυρου στα οποία δεν τοποθετήθηκε ντόμινο. (Με τα γωνιακά κελιά είμαστε πάντα εντάξει.) Μπορούμε τώρα να δούμε ότι μπορούμε να τοποθετήσουμε ντόμινο εναλλάξ στον περίγυρο του εσωτερικού
πίνακας στον περίγυρο του οποίου δεν θα τοποθετήσουμε κανένα ντόμινο. Στο σχήμα έχουμε σημειώσει τα κελιά τα οποία ακόμη δεν έχουν τη ζητούμενη ιδιότητα. Αυτά είναι ακριβώς τα κελιά τα οποία δεν είναι γωνιακά και είναι γειτονικά σε κελιά του αρχικού περίγυρου στα οποία δεν τοποθετήθηκε ντόμινο. (Με τα γωνιακά κελιά είμαστε πάντα εντάξει.) Μπορούμε τώρα να δούμε ότι μπορούμε να τοποθετήσουμε ντόμινο εναλλάξ στον περίγυρο του εσωτερικού  πίνακα ώστε να καλύπτουν ακριβώς τα ακάλυπτα κελιά του περίγυρου του
πίνακα ώστε να καλύπτουν ακριβώς τα ακάλυπτα κελιά του περίγυρου του 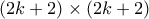 πίνακα. Η κάλυψη του
πίνακα. Η κάλυψη του  πίνακα συμπληρώνεται επαγωγικά.
πίνακα συμπληρώνεται επαγωγικά.Σημείωση: Οι περιπτώσεις
 περιττός και
περιττός και  άρτιος έχουν λίγο διαφορετικό σχήμα αλλά τίποτα το ουσιαστικά διαφορετικό.
άρτιος έχουν λίγο διαφορετικό σχήμα αλλά τίποτα το ουσιαστικά διαφορετικό.![\begin{tikzpicture}[scale=0.8,line cap=round,line join=round,>=triangle 45,x=1.0cm,y=1.0cm]
\clip(-0.98,-0.76) rectangle (10.96,10.66);
\fill[line width=2.pt,fill=black,fill opacity=1.0] (0.,8.) -- (1.,8.) -- (1.,10.) -- (0.,10.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (0.,6.) -- (1.,6.) -- (1.,4.) -- (0.,4.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (0.,2.) -- (0.,0.) -- (1.,0.) -- (1.,2.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (3.,1.) -- (3.,0.) -- (5.,0.) -- (5.,1.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (7.,1.) -- (7.,0.) -- (9.,0.) -- (9.,1.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (9.,2.) -- (10.,2.) -- (10.,4.) -- (9.,4.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (9.,6.) -- (10.,6.) -- (10.,8.) -- (9.,8.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (9.,9.) -- (9.,10.) -- (7.,10.) -- (7.,9.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (5.,9.) -- (5.,10.) -- (3.,10.) -- (3.,9.) -- cycle;
\draw [line width=2.pt] (0.,0.)-- (0.,10.);
\draw [line width=2.pt] (0.,10.)-- (10.,10.);
\draw [line width=2.pt] (10.,10.)-- (10.,0.);
\draw [line width=2.pt] (10.,0.)-- (0.,0.);
\draw [line width=2.pt] (1.,1.)-- (1.,9.);
\draw [line width=2.pt] (1.,9.)-- (9.,9.);
\draw [line width=2.pt] (9.,9.)-- (9.,1.);
\draw [line width=2.pt] (9.,1.)-- (1.,1.);
\draw [line width=2.pt] (0.,8.)-- (1.,8.);
\draw [line width=2.pt] (1.,8.)-- (1.,10.);
\draw [line width=2.pt] (1.,10.)-- (0.,10.);
\draw [line width=2.pt] (0.,10.)-- (0.,8.);
\draw [line width=2.pt] (0.,6.)-- (1.,6.);
\draw [line width=2.pt] (1.,6.)-- (1.,4.);
\draw [line width=2.pt] (1.,4.)-- (0.,4.);
\draw [line width=2.pt] (0.,4.)-- (0.,6.);
\draw [line width=2.pt] (0.,2.)-- (0.,0.);
\draw [line width=2.pt] (0.,0.)-- (1.,0.);
\draw [line width=2.pt] (1.,0.)-- (1.,2.);
\draw [line width=2.pt] (1.,2.)-- (0.,2.);
\draw [line width=2.pt] (3.,1.)-- (3.,0.);
\draw [line width=2.pt] (3.,0.)-- (5.,0.);
\draw [line width=2.pt] (5.,0.)-- (5.,1.);
\draw [line width=2.pt] (5.,1.)-- (3.,1.);
\draw [line width=2.pt] (7.,1.)-- (7.,0.);
\draw [line width=2.pt] (7.,0.)-- (9.,0.);
\draw [line width=2.pt] (9.,0.)-- (9.,1.);
\draw [line width=2.pt] (9.,1.)-- (7.,1.);
\draw [line width=2.pt] (9.,2.)-- (10.,2.);
\draw [line width=2.pt] (10.,2.)-- (10.,4.);
\draw [line width=2.pt] (10.,4.)-- (9.,4.);
\draw [line width=2.pt] (9.,4.)-- (9.,2.);
\draw [line width=2.pt] (9.,6.)-- (10.,6.);
\draw [line width=2.pt] (10.,6.)-- (10.,8.);
\draw [line width=2.pt] (10.,8.)-- (9.,8.);
\draw [line width=2.pt] (9.,8.)-- (9.,6.);
\draw [line width=2.pt] (9.,9.)-- (9.,10.);
\draw [line width=2.pt] (9.,10.)-- (7.,10.);
\draw [line width=2.pt] (7.,10.)-- (7.,9.);
\draw [line width=2.pt] (7.,9.)-- (9.,9.);
\draw [line width=2.pt] (5.,9.)-- (5.,10.);
\draw [line width=2.pt] (5.,10.)-- (3.,10.);
\draw [line width=2.pt] (3.,10.)-- (3.,9.);
\draw [line width=2.pt] (3.,9.)-- (5.,9.);
\draw [line width=2.pt] (2.,8.)-- (2.,2.);
\draw [line width=2.pt] (2.,8.)-- (8.,8.);
\draw [line width=2.pt] (8.,8.)-- (8.,2.);
\draw [line width=2.pt] (8.,2.)-- (2.,2.);
\draw [fill=black] (1.5,7.5) circle (2.0pt);
\draw [fill= black] (1.5,6.5) circle (2.0pt);
\draw [fill= black] (2.5,8.5) circle (2.0pt);
\draw [fill= black] (1.5,3.5) circle (2.0pt);
\draw [fill= black] (1.5,2.5) circle (2.0pt);
\draw [fill= black] (5.5,8.5) circle (2.0pt);
\draw [fill= black] (6.5,8.5) circle (2.0pt);
\draw [fill= black] (8.5,5.5) circle (2.0pt);
\draw [fill= black] (8.5,4.5) circle (2.0pt);
\draw [fill= black] (6.5,1.5) circle (2.0pt);
\draw [fill= black] (5.5,1.5) circle (2.0pt);
\draw [fill= black] (2.5,1.5) circle (2.0pt);
\end{tikzpicture}
\begin{tikzpicture}[scale=0.8,line cap=round,line join=round,>=triangle 45,x=1.0cm,y=1.0cm]
\clip(-0.98,-0.76) rectangle (10.96,10.66);
\fill[line width=2.pt,fill=black,fill opacity=1.0] (0.,8.) -- (1.,8.) -- (1.,10.) -- (0.,10.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (0.,6.) -- (1.,6.) -- (1.,4.) -- (0.,4.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (0.,2.) -- (0.,0.) -- (1.,0.) -- (1.,2.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (3.,1.) -- (3.,0.) -- (5.,0.) -- (5.,1.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (7.,1.) -- (7.,0.) -- (9.,0.) -- (9.,1.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (9.,2.) -- (10.,2.) -- (10.,4.) -- (9.,4.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (9.,6.) -- (10.,6.) -- (10.,8.) -- (9.,8.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (9.,9.) -- (9.,10.) -- (7.,10.) -- (7.,9.) -- cycle;
\fill[line width=2.pt,fill=black,fill opacity=1.0] (5.,9.) -- (5.,10.) -- (3.,10.) -- (3.,9.) -- cycle;
\draw [line width=2.pt] (0.,0.)-- (0.,10.);
\draw [line width=2.pt] (0.,10.)-- (10.,10.);
\draw [line width=2.pt] (10.,10.)-- (10.,0.);
\draw [line width=2.pt] (10.,0.)-- (0.,0.);
\draw [line width=2.pt] (1.,1.)-- (1.,9.);
\draw [line width=2.pt] (1.,9.)-- (9.,9.);
\draw [line width=2.pt] (9.,9.)-- (9.,1.);
\draw [line width=2.pt] (9.,1.)-- (1.,1.);
\draw [line width=2.pt] (0.,8.)-- (1.,8.);
\draw [line width=2.pt] (1.,8.)-- (1.,10.);
\draw [line width=2.pt] (1.,10.)-- (0.,10.);
\draw [line width=2.pt] (0.,10.)-- (0.,8.);
\draw [line width=2.pt] (0.,6.)-- (1.,6.);
\draw [line width=2.pt] (1.,6.)-- (1.,4.);
\draw [line width=2.pt] (1.,4.)-- (0.,4.);
\draw [line width=2.pt] (0.,4.)-- (0.,6.);
\draw [line width=2.pt] (0.,2.)-- (0.,0.);
\draw [line width=2.pt] (0.,0.)-- (1.,0.);
\draw [line width=2.pt] (1.,0.)-- (1.,2.);
\draw [line width=2.pt] (1.,2.)-- (0.,2.);
\draw [line width=2.pt] (3.,1.)-- (3.,0.);
\draw [line width=2.pt] (3.,0.)-- (5.,0.);
\draw [line width=2.pt] (5.,0.)-- (5.,1.);
\draw [line width=2.pt] (5.,1.)-- (3.,1.);
\draw [line width=2.pt] (7.,1.)-- (7.,0.);
\draw [line width=2.pt] (7.,0.)-- (9.,0.);
\draw [line width=2.pt] (9.,0.)-- (9.,1.);
\draw [line width=2.pt] (9.,1.)-- (7.,1.);
\draw [line width=2.pt] (9.,2.)-- (10.,2.);
\draw [line width=2.pt] (10.,2.)-- (10.,4.);
\draw [line width=2.pt] (10.,4.)-- (9.,4.);
\draw [line width=2.pt] (9.,4.)-- (9.,2.);
\draw [line width=2.pt] (9.,6.)-- (10.,6.);
\draw [line width=2.pt] (10.,6.)-- (10.,8.);
\draw [line width=2.pt] (10.,8.)-- (9.,8.);
\draw [line width=2.pt] (9.,8.)-- (9.,6.);
\draw [line width=2.pt] (9.,9.)-- (9.,10.);
\draw [line width=2.pt] (9.,10.)-- (7.,10.);
\draw [line width=2.pt] (7.,10.)-- (7.,9.);
\draw [line width=2.pt] (7.,9.)-- (9.,9.);
\draw [line width=2.pt] (5.,9.)-- (5.,10.);
\draw [line width=2.pt] (5.,10.)-- (3.,10.);
\draw [line width=2.pt] (3.,10.)-- (3.,9.);
\draw [line width=2.pt] (3.,9.)-- (5.,9.);
\draw [line width=2.pt] (2.,8.)-- (2.,2.);
\draw [line width=2.pt] (2.,8.)-- (8.,8.);
\draw [line width=2.pt] (8.,8.)-- (8.,2.);
\draw [line width=2.pt] (8.,2.)-- (2.,2.);
\draw [fill=black] (1.5,7.5) circle (2.0pt);
\draw [fill= black] (1.5,6.5) circle (2.0pt);
\draw [fill= black] (2.5,8.5) circle (2.0pt);
\draw [fill= black] (1.5,3.5) circle (2.0pt);
\draw [fill= black] (1.5,2.5) circle (2.0pt);
\draw [fill= black] (5.5,8.5) circle (2.0pt);
\draw [fill= black] (6.5,8.5) circle (2.0pt);
\draw [fill= black] (8.5,5.5) circle (2.0pt);
\draw [fill= black] (8.5,4.5) circle (2.0pt);
\draw [fill= black] (6.5,1.5) circle (2.0pt);
\draw [fill= black] (5.5,1.5) circle (2.0pt);
\draw [fill= black] (2.5,1.5) circle (2.0pt);
\end{tikzpicture}](/forum/ext/geomar/texintegr/latexrender/pictures/ba77d6b6db28f7cc72a2d7df6a37fab0.png)
Re: EGMO 2019
Και μια λίγο διαφορετική σκέψη γι' αυτό.
Αν κάποιος είναι μηδέν, ας πούμε
 , τότε
, τότε  από την πρώτη συνθήκη και
από την πρώτη συνθήκη και  από τη δεύτερη,
από τη δεύτερη,άρα
 ή
ή  .
.Αλλιώς, κάνω ομογενή τη δεύτερη συνθήκη, χρησιμοποιώντας την πρώτη:

Επειδή τώρα έχουμε υποθέσει ότι όλοι είναι διάφοροι του μηδενός, παίρνουμε
 .
.Παίρνοντας κυκλικά τις άλλες δύο σχέσεις και προσθέτοντας έχουμε
 , οπότε
, οπότε  .
.Σιλουανός Μπραζιτίκος
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
Re: EGMO 2019
Πρόβλημα 4: Έστω  τρίγωνο με έγκεντρο
τρίγωνο με έγκεντρο  . Ο κύκλος ο οποίος διέρχεται από το
. Ο κύκλος ο οποίος διέρχεται από το  και εφάπτεται της
και εφάπτεται της  στο
στο  τέμνει ξανά την πλευρά
τέμνει ξανά την πλευρά  στο
στο  Ο κύκλος ο οποίος διέρχεται από το
Ο κύκλος ο οποίος διέρχεται από το  και εφάπτεται της
και εφάπτεται της  στο
στο  τέμνει ξανά την πλευρά
τέμνει ξανά την πλευρά  στο
στο  Να αποδειχθεί ότι η
Να αποδειχθεί ότι η  εφάπτεται στον εγγεγραμμένο κύκλο του
εφάπτεται στον εγγεγραμμένο κύκλο του 
Πρόβλημα 5: Έστω ένας ακέραιος, και έστω
ένας ακέραιος, και έστω  θετικοί ακέραιοι. Να αποδειχθεί ότι υπάρχουν θετικοί ακέραιοι
θετικοί ακέραιοι. Να αποδειχθεί ότι υπάρχουν θετικοί ακέραιοι 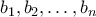 οι οποίοι να ικανοποιούν τις ακόλουθες τρεις συνθήκες:
οι οποίοι να ικανοποιούν τις ακόλουθες τρεις συνθήκες:
(Α) για
για  ,
,
(Β) τα υπόλοιπα των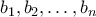 όταν διαιρεθούν με τον
όταν διαιρεθούν με τον  είναι ανά δύο διαφορετικά, και
είναι ανά δύο διαφορετικά, και
(Γ)
(Εδώ, το συμβολίζει το ακέραιο μέρος του πραγματικού αριθμού
συμβολίζει το ακέραιο μέρος του πραγματικού αριθμού  , δηλαδή, τον μεγαλύτερο ακέραιο ο οποίος δεν υπερβαίνει τον
, δηλαδή, τον μεγαλύτερο ακέραιο ο οποίος δεν υπερβαίνει τον  .)
.)
Πρόβλημα 6:
Σε έναν κύκλο η Αλίνα σχεδιάζει χορδές, τα άκρα των οποίων είναι όλα διαφορετικά. Ένα σημείο θεωρείται σημαδεμένο εάν είναι είτε
χορδές, τα άκρα των οποίων είναι όλα διαφορετικά. Ένα σημείο θεωρείται σημαδεμένο εάν είναι είτε
(i) ένα από τα άκρα των χορδών, είτε
άκρα των χορδών, είτε
(ii) ένα σημείο τομής τουλάχιστον δύο χορδών.
Η Αλίνα βάζει έναν αριθμό σε κάθε σημαδεμένο σημείο. Από τα σημεία τα οποία ικανοποιούν το κριτήριο (i), η Αλίνα βάζει σε
σημεία τα οποία ικανοποιούν το κριτήριο (i), η Αλίνα βάζει σε  σημεία το
σημεία το  και στα υπόλοιπα
και στα υπόλοιπα  σημεία το
σημεία το 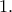
Σε κάθε σημείο το οποίο ικανοποιεί το κριτήριο (ii) βάζει έναν αυθαίρετο ακέραιο (όχι απαραίτητα θετικό).
Κατά μήκος κάθε χορδής, η Αλίνα θεωρεί τα τμήματα τα οποία συνδέουν δύο διαδοχικά σημαδεμένα σημεία. (Μια χορδή με σημαδεμένα σημεία έχει
σημαδεμένα σημεία έχει  τέτοια τμήματα.) Σε κάθε τέτοιο τμήμα βάζει μια κίτρινη ετικέτα με το άθροισμα των αριθμών των άκρων του και μια μπλε ετικέτα με την απόλυτη τιμή της διαφοράς των αριθμών των άκρων του.
τέτοια τμήματα.) Σε κάθε τέτοιο τμήμα βάζει μια κίτρινη ετικέτα με το άθροισμα των αριθμών των άκρων του και μια μπλε ετικέτα με την απόλυτη τιμή της διαφοράς των αριθμών των άκρων του.
Η Αλίνα παρατηρεί ότι οι κίτρινες ετικέτες λαμβάνουν κάθε μια από τις τιμές
κίτρινες ετικέτες λαμβάνουν κάθε μια από τις τιμές  ακριβώς μια φορά. Να αποδειχθεί ότι η τιμή τουλάχιστον μιας μπλε ετικέτας είναι πολλαπλάσιο του
ακριβώς μια φορά. Να αποδειχθεί ότι η τιμή τουλάχιστον μιας μπλε ετικέτας είναι πολλαπλάσιο του  .
.
(Χορδή είναι ένα ευθύγραμμο τμήμα το οποίο συνδέει δύο διαφορετικά σημεία ενός κύκλου.)
 τρίγωνο με έγκεντρο
τρίγωνο με έγκεντρο  . Ο κύκλος ο οποίος διέρχεται από το
. Ο κύκλος ο οποίος διέρχεται από το  και εφάπτεται της
και εφάπτεται της  στο
στο  τέμνει ξανά την πλευρά
τέμνει ξανά την πλευρά  στο
στο  Ο κύκλος ο οποίος διέρχεται από το
Ο κύκλος ο οποίος διέρχεται από το  και εφάπτεται της
και εφάπτεται της  στο
στο  τέμνει ξανά την πλευρά
τέμνει ξανά την πλευρά  στο
στο 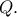 Να αποδειχθεί ότι η
Να αποδειχθεί ότι η  εφάπτεται στον εγγεγραμμένο κύκλο του
εφάπτεται στον εγγεγραμμένο κύκλο του 
Πρόβλημα 5: Έστω
 ένας ακέραιος, και έστω
ένας ακέραιος, και έστω  θετικοί ακέραιοι. Να αποδειχθεί ότι υπάρχουν θετικοί ακέραιοι
θετικοί ακέραιοι. Να αποδειχθεί ότι υπάρχουν θετικοί ακέραιοι 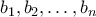 οι οποίοι να ικανοποιούν τις ακόλουθες τρεις συνθήκες:
οι οποίοι να ικανοποιούν τις ακόλουθες τρεις συνθήκες:(Α)
 για
για  ,
,(Β) τα υπόλοιπα των
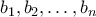 όταν διαιρεθούν με τον
όταν διαιρεθούν με τον  είναι ανά δύο διαφορετικά, και
είναι ανά δύο διαφορετικά, και(Γ)

(Εδώ, το
 συμβολίζει το ακέραιο μέρος του πραγματικού αριθμού
συμβολίζει το ακέραιο μέρος του πραγματικού αριθμού  , δηλαδή, τον μεγαλύτερο ακέραιο ο οποίος δεν υπερβαίνει τον
, δηλαδή, τον μεγαλύτερο ακέραιο ο οποίος δεν υπερβαίνει τον  .)
.)Πρόβλημα 6:
Σε έναν κύκλο η Αλίνα σχεδιάζει
 χορδές, τα άκρα των οποίων είναι όλα διαφορετικά. Ένα σημείο θεωρείται σημαδεμένο εάν είναι είτε
χορδές, τα άκρα των οποίων είναι όλα διαφορετικά. Ένα σημείο θεωρείται σημαδεμένο εάν είναι είτε(i) ένα από τα
 άκρα των χορδών, είτε
άκρα των χορδών, είτε(ii) ένα σημείο τομής τουλάχιστον δύο χορδών.
Η Αλίνα βάζει έναν αριθμό σε κάθε σημαδεμένο σημείο. Από τα
 σημεία τα οποία ικανοποιούν το κριτήριο (i), η Αλίνα βάζει σε
σημεία τα οποία ικανοποιούν το κριτήριο (i), η Αλίνα βάζει σε  σημεία το
σημεία το  και στα υπόλοιπα
και στα υπόλοιπα  σημεία το
σημεία το 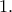
Σε κάθε σημείο το οποίο ικανοποιεί το κριτήριο (ii) βάζει έναν αυθαίρετο ακέραιο (όχι απαραίτητα θετικό).
Κατά μήκος κάθε χορδής, η Αλίνα θεωρεί τα τμήματα τα οποία συνδέουν δύο διαδοχικά σημαδεμένα σημεία. (Μια χορδή με
 σημαδεμένα σημεία έχει
σημαδεμένα σημεία έχει  τέτοια τμήματα.) Σε κάθε τέτοιο τμήμα βάζει μια κίτρινη ετικέτα με το άθροισμα των αριθμών των άκρων του και μια μπλε ετικέτα με την απόλυτη τιμή της διαφοράς των αριθμών των άκρων του.
τέτοια τμήματα.) Σε κάθε τέτοιο τμήμα βάζει μια κίτρινη ετικέτα με το άθροισμα των αριθμών των άκρων του και μια μπλε ετικέτα με την απόλυτη τιμή της διαφοράς των αριθμών των άκρων του.Η Αλίνα παρατηρεί ότι οι
 κίτρινες ετικέτες λαμβάνουν κάθε μια από τις τιμές
κίτρινες ετικέτες λαμβάνουν κάθε μια από τις τιμές  ακριβώς μια φορά. Να αποδειχθεί ότι η τιμή τουλάχιστον μιας μπλε ετικέτας είναι πολλαπλάσιο του
ακριβώς μια φορά. Να αποδειχθεί ότι η τιμή τουλάχιστον μιας μπλε ετικέτας είναι πολλαπλάσιο του  .
.(Χορδή είναι ένα ευθύγραμμο τμήμα το οποίο συνδέει δύο διαφορετικά σημεία ενός κύκλου.)
τελευταία επεξεργασία από Demetres σε Τετ Απρ 10, 2019 3:23 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Re: EGMO 2019
Πρόβλημα 4. Έστω  τρίγωνο με έγκεντρο
τρίγωνο με έγκεντρο  . Ο κύκλος ο οποίος διέρχεται από το
. Ο κύκλος ο οποίος διέρχεται από το  και εφάπτεται της
και εφάπτεται της  στο
στο  τέμνει ξανά την πλευρά
τέμνει ξανά την πλευρά  στο
στο  Ο κύκλος ο οποίος διέρχεται από το
Ο κύκλος ο οποίος διέρχεται από το  και εφάπτεται της
και εφάπτεται της  στο
στο  τέμνει ξανά την πλευρά
τέμνει ξανά την πλευρά  στο
στο 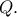 Να αποδειχθεί ότι η
Να αποδειχθεί ότι η  εφάπτεται στον εγγεγραμμένο κύκλο του
εφάπτεται στον εγγεγραμμένο κύκλο του 
************************************************************
Λύση: Από τη δύναμη σημείου ως προς κύκλο παίρνουμε
ως προς κύκλο παίρνουμε

Έτσι, το είναι εγγράψιμο, κι έτσι,
είναι εγγράψιμο, κι έτσι, 
Έστω το περίκεντρο του
το περίκεντρο του  και έστω
και έστω  το περίκεντρο του
το περίκεντρο του  . Τότε η
. Τότε η  είναι κάθετη στην
είναι κάθετη στην  στο
στο 
Έστω το σημείο τομής της
το σημείο τομής της  με την
με την  Τότε από το ορθογώνιο τρίγωνο
Τότε από το ορθογώνιο τρίγωνο  , έχουμε
, έχουμε
 και από το θεώρημα εξωτερικής γωνίας στο
και από το θεώρημα εξωτερικής γωνίας στο 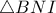 , έχουμε
, έχουμε 
Έτσι

Επομένως, αφού η εφάπτεται στον περίκεντρο του
εφάπτεται στον περίκεντρο του  στο
στο  έχουμε
έχουμε

Αφού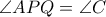 , έχουμε
, έχουμε

επίσης. Άρα το βρίσκεται στη διχοτόμο της
βρίσκεται στη διχοτόμο της  , και άρα θα ισαπέχει από τις πλευρές της. Έτσι, η απόσταση του
, και άρα θα ισαπέχει από τις πλευρές της. Έτσι, η απόσταση του  από το
από το  ισούται με την ακτίνα του εγγεγραμένου κύκλου στο
ισούται με την ακτίνα του εγγεγραμένου κύκλου στο 
Συνεπώς, η εφάπτεται στον εγγεγραμμένο κύκλο του
εφάπτεται στον εγγεγραμμένο κύκλο του 
 τρίγωνο με έγκεντρο
τρίγωνο με έγκεντρο  . Ο κύκλος ο οποίος διέρχεται από το
. Ο κύκλος ο οποίος διέρχεται από το  και εφάπτεται της
και εφάπτεται της  στο
στο  τέμνει ξανά την πλευρά
τέμνει ξανά την πλευρά  στο
στο  Ο κύκλος ο οποίος διέρχεται από το
Ο κύκλος ο οποίος διέρχεται από το  και εφάπτεται της
και εφάπτεται της  στο
στο  τέμνει ξανά την πλευρά
τέμνει ξανά την πλευρά  στο
στο 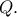 Να αποδειχθεί ότι η
Να αποδειχθεί ότι η  εφάπτεται στον εγγεγραμμένο κύκλο του
εφάπτεται στον εγγεγραμμένο κύκλο του 
************************************************************
Λύση: Από τη δύναμη σημείου
 ως προς κύκλο παίρνουμε
ως προς κύκλο παίρνουμε
Έτσι, το
 είναι εγγράψιμο, κι έτσι,
είναι εγγράψιμο, κι έτσι, 
Έστω
 το περίκεντρο του
το περίκεντρο του  και έστω
και έστω  το περίκεντρο του
το περίκεντρο του  . Τότε η
. Τότε η  είναι κάθετη στην
είναι κάθετη στην  στο
στο 
Έστω
 το σημείο τομής της
το σημείο τομής της  με την
με την  Τότε από το ορθογώνιο τρίγωνο
Τότε από το ορθογώνιο τρίγωνο  , έχουμε
, έχουμε και από το θεώρημα εξωτερικής γωνίας στο
και από το θεώρημα εξωτερικής γωνίας στο 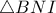 , έχουμε
, έχουμε 
Έτσι

Επομένως, αφού η
 εφάπτεται στον περίκεντρο του
εφάπτεται στον περίκεντρο του  στο
στο  έχουμε
έχουμε
Αφού
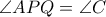 , έχουμε
, έχουμε
επίσης. Άρα το
 βρίσκεται στη διχοτόμο της
βρίσκεται στη διχοτόμο της  , και άρα θα ισαπέχει από τις πλευρές της. Έτσι, η απόσταση του
, και άρα θα ισαπέχει από τις πλευρές της. Έτσι, η απόσταση του  από το
από το  ισούται με την ακτίνα του εγγεγραμένου κύκλου στο
ισούται με την ακτίνα του εγγεγραμένου κύκλου στο 
Συνεπώς, η
 εφάπτεται στον εγγεγραμμένο κύκλο του
εφάπτεται στον εγγεγραμμένο κύκλο του 
- Συνημμένα
-
- egmo_4_mathematica.png (25.97 KiB) Προβλήθηκε 2157 φορές
Re: EGMO 2019
Πρόβλημα 5. Έστω  ένας ακέραιος, και έστω
ένας ακέραιος, και έστω  θετικοί ακέραιοι. Να αποδειχθεί ότι υπάρχουν θετικοί ακέραιοι
θετικοί ακέραιοι. Να αποδειχθεί ότι υπάρχουν θετικοί ακέραιοι 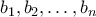 οι οποίοι να ικανοποιούν τις ακόλουθες τρεις συνθήκες:
οι οποίοι να ικανοποιούν τις ακόλουθες τρεις συνθήκες:
(i) για
για  ,
,
(ii) τα υπόλοιπα των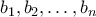 όταν διαιρεθούν με τον
όταν διαιρεθούν με τον  είναι ανά δύο διαφορετικά, και
είναι ανά δύο διαφορετικά, και
(iii)
****************************
Λύση: Θέτουμε . Ορίζουμε τα
. Ορίζουμε τα  επαγωγικά ως εξής: ας υποθέσουμε ότι έχουμε κατασκευάσει τα
επαγωγικά ως εξής: ας υποθέσουμε ότι έχουμε κατασκευάσει τα  για κάποια
για κάποια 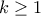 ώστε να ικανοποιούν τις συνθήκες. Παρατηρούμε ότι τουλάχιστον ένας από τους
ώστε να ικανοποιούν τις συνθήκες. Παρατηρούμε ότι τουλάχιστον ένας από τους  ακέραιους
ακέραιους  αφήνει διαφορετικό υπόλοιπο στη διαίρεση του με το
αφήνει διαφορετικό υπόλοιπο στη διαίρεση του με το  από το υπόλοιπο που αφήνουν οι
από το υπόλοιπο που αφήνουν οι  Θέτουμε
Θέτουμε  να είναι ο ελάχιστος από αυτούς τους αριθμούς. Έτσι
να είναι ο ελάχιστος από αυτούς τους αριθμούς. Έτσι

for .Τότε οι πρώτες δύο συνθήκες ικανοποιούνται από την κατασκευή μας. Για την τρίτη συνθήκη, προσθέτοντας τις παρακάτω σχέσεις κατά μέλη
.Τότε οι πρώτες δύο συνθήκες ικανοποιούνται από την κατασκευή μας. Για την τρίτη συνθήκη, προσθέτοντας τις παρακάτω σχέσεις κατά μέλη

παίρνουμε

Το αριστερό μέλος της παραπάνω ανισότητας είναι πολλαπλάσιο του από τη συνθήκη (ii). Διαιρώντας με
από τη συνθήκη (ii). Διαιρώντας με  , αφού
, αφού  , παίρνουμε
, παίρνουμε

Το αριστερό μέλος της παραπάνω ανισότητας είναι ακέραιος, οπότε παίρνοντας το ακέραιο μέρος και των δυο μελών έχουμε

όπως θέλαμε.
Φιλικά,
Αχιλλέας
 ένας ακέραιος, και έστω
ένας ακέραιος, και έστω  θετικοί ακέραιοι. Να αποδειχθεί ότι υπάρχουν θετικοί ακέραιοι
θετικοί ακέραιοι. Να αποδειχθεί ότι υπάρχουν θετικοί ακέραιοι 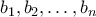 οι οποίοι να ικανοποιούν τις ακόλουθες τρεις συνθήκες:
οι οποίοι να ικανοποιούν τις ακόλουθες τρεις συνθήκες:(i)
 για
για  ,
,(ii) τα υπόλοιπα των
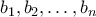 όταν διαιρεθούν με τον
όταν διαιρεθούν με τον  είναι ανά δύο διαφορετικά, και
είναι ανά δύο διαφορετικά, και(iii)

****************************
Λύση: Θέτουμε
 . Ορίζουμε τα
. Ορίζουμε τα  επαγωγικά ως εξής: ας υποθέσουμε ότι έχουμε κατασκευάσει τα
επαγωγικά ως εξής: ας υποθέσουμε ότι έχουμε κατασκευάσει τα  για κάποια
για κάποια 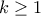 ώστε να ικανοποιούν τις συνθήκες. Παρατηρούμε ότι τουλάχιστον ένας από τους
ώστε να ικανοποιούν τις συνθήκες. Παρατηρούμε ότι τουλάχιστον ένας από τους  ακέραιους
ακέραιους  αφήνει διαφορετικό υπόλοιπο στη διαίρεση του με το
αφήνει διαφορετικό υπόλοιπο στη διαίρεση του με το  από το υπόλοιπο που αφήνουν οι
από το υπόλοιπο που αφήνουν οι  Θέτουμε
Θέτουμε  να είναι ο ελάχιστος από αυτούς τους αριθμούς. Έτσι
να είναι ο ελάχιστος από αυτούς τους αριθμούς. Έτσι
for
 .Τότε οι πρώτες δύο συνθήκες ικανοποιούνται από την κατασκευή μας. Για την τρίτη συνθήκη, προσθέτοντας τις παρακάτω σχέσεις κατά μέλη
.Τότε οι πρώτες δύο συνθήκες ικανοποιούνται από την κατασκευή μας. Για την τρίτη συνθήκη, προσθέτοντας τις παρακάτω σχέσεις κατά μέλη
παίρνουμε

Το αριστερό μέλος της παραπάνω ανισότητας είναι πολλαπλάσιο του
 από τη συνθήκη (ii). Διαιρώντας με
από τη συνθήκη (ii). Διαιρώντας με  , αφού
, αφού  , παίρνουμε
, παίρνουμε
Το αριστερό μέλος της παραπάνω ανισότητας είναι ακέραιος, οπότε παίρνοντας το ακέραιο μέρος και των δυο μελών έχουμε

όπως θέλαμε.
Φιλικά,
Αχιλλέας
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: EGMO 2019
2η (και τελευταία μέρα του διαγωνισμού). Εύχομαι καλά αποτελέσματα στις ομάδες μας!
Πρόβλημα 4
Έστω τρίγωνο με έγκεντρο
τρίγωνο με έγκεντρο  . Ο κύκλος ο οποίος διέρχεται από το
. Ο κύκλος ο οποίος διέρχεται από το  και εφάπτεται της
και εφάπτεται της  στο
στο  τέμνει ξανά την πλευρά
τέμνει ξανά την πλευρά  στο
στο  Ο κύκλος ο οποίος διέρχεται από το
Ο κύκλος ο οποίος διέρχεται από το  και εφάπτεται της
και εφάπτεται της  στο
στο  τέμνει ξανά την πλευρά
τέμνει ξανά την πλευρά  στο
στο 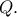 Να αποδειχθεί ότι η
Να αποδειχθεί ότι η  εφάπτεται στον εγγεγραμμένο κύκλο του
εφάπτεται στον εγγεγραμμένο κύκλο του 
Πρόβλημα 5
Έστω ένας ακέραιος, και έστω
ένας ακέραιος, και έστω  θετικοί ακέραιοι. Να αποδειχθεί ότι υπάρχουν θετικοί ακέραιοι
θετικοί ακέραιοι. Να αποδειχθεί ότι υπάρχουν θετικοί ακέραιοι 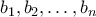 οι οποίοι να ικανοποιούν τις ακόλουθες τρεις συνθήκες:
οι οποίοι να ικανοποιούν τις ακόλουθες τρεις συνθήκες:
(Α) για
για  ,
,
(Β) τα υπόλοιπα των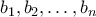 όταν διαιρεθούν με τον
όταν διαιρεθούν με τον  είναι ανά δύο διαφορετικά, και
είναι ανά δύο διαφορετικά, και
(Γ)
(Εδώ, το συμβολίζει το ακέραιο μέρος του πραγματικού αριθμού
συμβολίζει το ακέραιο μέρος του πραγματικού αριθμού  , δηλαδή, τον μεγαλύτερο ακέραιο ο οποίος δεν υπερβαίνει τον
, δηλαδή, τον μεγαλύτερο ακέραιο ο οποίος δεν υπερβαίνει τον  .)
.)
Πρόβλημα 6
Σε έναν κύκλο η Αλίνα σχεδιάζει χορδές, τα άκρα των οποίων είναι όλα διαφορετικά. Ένα σημείο θεωρείται σημαδεμένο εάν είναι είτε
χορδές, τα άκρα των οποίων είναι όλα διαφορετικά. Ένα σημείο θεωρείται σημαδεμένο εάν είναι είτε
(i) ένα από τα άκρα των χορδών, είτε
άκρα των χορδών, είτε
(ii) ένα σημείο τομής τουλάχιστον δύο χορδών.
Η Αλίνα βάζει έναν αριθμό σε κάθε σημαδεμένο σημείο. Από τα σημεία τα οποία ικανοποιούν το κριτήριο (i), η Αλίνα βάζει σε
σημεία τα οποία ικανοποιούν το κριτήριο (i), η Αλίνα βάζει σε  σημεία το
σημεία το  και στα υπόλοιπα
και στα υπόλοιπα  σημεία το
σημεία το 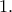
Σε κάθε σημείο το οποίο ικανοποιεί το κριτήριο (ii) βάζει έναν αυθαίρετο ακέραιο (όχι απαραίτητα θετικό).
Κατά μήκος κάθε χορδής, η Αλίνα θεωρεί τα τμήματα τα οποία συνδέουν δύο διαδοχικά σημαδεμένα σημεία. (Μια χορδή με σημαδεμένα σημεία έχει
σημαδεμένα σημεία έχει  τέτοια τμήματα.) Σε κάθε τέτοιο τμήμα βάζει μια κίτρινη ετικέτα με το άθροισμα των αριθμών των άκρων του και μια μπλε ετικέτα με την απόλυτη τιμή της διαφοράς των αριθμών των άκρων του.
τέτοια τμήματα.) Σε κάθε τέτοιο τμήμα βάζει μια κίτρινη ετικέτα με το άθροισμα των αριθμών των άκρων του και μια μπλε ετικέτα με την απόλυτη τιμή της διαφοράς των αριθμών των άκρων του.
Η Αλίνα παρατηρεί ότι οι κίτρινες ετικέτες λαμβάνουν κάθε μια από τις τιμές
κίτρινες ετικέτες λαμβάνουν κάθε μια από τις τιμές  ακριβώς μια φορά. Να αποδειχθεί ότι η τιμή τουλάχιστον μιας μπλε ετικέτας είναι πολλαπλάσιο του
ακριβώς μια φορά. Να αποδειχθεί ότι η τιμή τουλάχιστον μιας μπλε ετικέτας είναι πολλαπλάσιο του  .
.
(Χορδή είναι ένα ευθύγραμμο τμήμα το οποίο συνδέει δύο διαφορετικά σημεία ενός κύκλου.)
Πρόβλημα 4
Έστω
 τρίγωνο με έγκεντρο
τρίγωνο με έγκεντρο  . Ο κύκλος ο οποίος διέρχεται από το
. Ο κύκλος ο οποίος διέρχεται από το  και εφάπτεται της
και εφάπτεται της  στο
στο  τέμνει ξανά την πλευρά
τέμνει ξανά την πλευρά  στο
στο  Ο κύκλος ο οποίος διέρχεται από το
Ο κύκλος ο οποίος διέρχεται από το  και εφάπτεται της
και εφάπτεται της  στο
στο  τέμνει ξανά την πλευρά
τέμνει ξανά την πλευρά  στο
στο 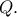 Να αποδειχθεί ότι η
Να αποδειχθεί ότι η  εφάπτεται στον εγγεγραμμένο κύκλο του
εφάπτεται στον εγγεγραμμένο κύκλο του 
Πρόβλημα 5
Έστω
 ένας ακέραιος, και έστω
ένας ακέραιος, και έστω  θετικοί ακέραιοι. Να αποδειχθεί ότι υπάρχουν θετικοί ακέραιοι
θετικοί ακέραιοι. Να αποδειχθεί ότι υπάρχουν θετικοί ακέραιοι 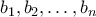 οι οποίοι να ικανοποιούν τις ακόλουθες τρεις συνθήκες:
οι οποίοι να ικανοποιούν τις ακόλουθες τρεις συνθήκες:(Α)
 για
για  ,
,(Β) τα υπόλοιπα των
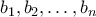 όταν διαιρεθούν με τον
όταν διαιρεθούν με τον  είναι ανά δύο διαφορετικά, και
είναι ανά δύο διαφορετικά, και(Γ)

(Εδώ, το
 συμβολίζει το ακέραιο μέρος του πραγματικού αριθμού
συμβολίζει το ακέραιο μέρος του πραγματικού αριθμού  , δηλαδή, τον μεγαλύτερο ακέραιο ο οποίος δεν υπερβαίνει τον
, δηλαδή, τον μεγαλύτερο ακέραιο ο οποίος δεν υπερβαίνει τον  .)
.)Πρόβλημα 6
Σε έναν κύκλο η Αλίνα σχεδιάζει
 χορδές, τα άκρα των οποίων είναι όλα διαφορετικά. Ένα σημείο θεωρείται σημαδεμένο εάν είναι είτε
χορδές, τα άκρα των οποίων είναι όλα διαφορετικά. Ένα σημείο θεωρείται σημαδεμένο εάν είναι είτε(i) ένα από τα
 άκρα των χορδών, είτε
άκρα των χορδών, είτε(ii) ένα σημείο τομής τουλάχιστον δύο χορδών.
Η Αλίνα βάζει έναν αριθμό σε κάθε σημαδεμένο σημείο. Από τα
 σημεία τα οποία ικανοποιούν το κριτήριο (i), η Αλίνα βάζει σε
σημεία τα οποία ικανοποιούν το κριτήριο (i), η Αλίνα βάζει σε  σημεία το
σημεία το  και στα υπόλοιπα
και στα υπόλοιπα  σημεία το
σημεία το 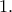
Σε κάθε σημείο το οποίο ικανοποιεί το κριτήριο (ii) βάζει έναν αυθαίρετο ακέραιο (όχι απαραίτητα θετικό).
Κατά μήκος κάθε χορδής, η Αλίνα θεωρεί τα τμήματα τα οποία συνδέουν δύο διαδοχικά σημαδεμένα σημεία. (Μια χορδή με
 σημαδεμένα σημεία έχει
σημαδεμένα σημεία έχει  τέτοια τμήματα.) Σε κάθε τέτοιο τμήμα βάζει μια κίτρινη ετικέτα με το άθροισμα των αριθμών των άκρων του και μια μπλε ετικέτα με την απόλυτη τιμή της διαφοράς των αριθμών των άκρων του.
τέτοια τμήματα.) Σε κάθε τέτοιο τμήμα βάζει μια κίτρινη ετικέτα με το άθροισμα των αριθμών των άκρων του και μια μπλε ετικέτα με την απόλυτη τιμή της διαφοράς των αριθμών των άκρων του.Η Αλίνα παρατηρεί ότι οι
 κίτρινες ετικέτες λαμβάνουν κάθε μια από τις τιμές
κίτρινες ετικέτες λαμβάνουν κάθε μια από τις τιμές  ακριβώς μια φορά. Να αποδειχθεί ότι η τιμή τουλάχιστον μιας μπλε ετικέτας είναι πολλαπλάσιο του
ακριβώς μια φορά. Να αποδειχθεί ότι η τιμή τουλάχιστον μιας μπλε ετικέτας είναι πολλαπλάσιο του  .
.(Χορδή είναι ένα ευθύγραμμο τμήμα το οποίο συνδέει δύο διαφορετικά σημεία ενός κύκλου.)
Αλέξανδρος Συγκελάκης
Re: EGMO 2019
Λίγο διαφορετικά.Τσιαλας Νικολαος έγραψε: ↑Τετ Απρ 10, 2019 3:05 pmΠρόβλημα 4: Έστωτρίγωνο με έγκεντρο
. Ο κύκλος ο οποίος διέρχεται από το
και εφάπτεται της
στο
τέμνει ξανά την πλευρά
στο
Ο κύκλος ο οποίος διέρχεται από το
και εφάπτεται της
στο
τέμνει ξανά την πλευρά
στο
Να αποδειχθεί ότι η
εφάπτεται στον εγγεγραμμένο κύκλο του

Aπό τις γωνίες χορδής και εφαπτομένης έχουμε
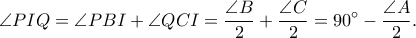
Όμως το
 είναι και στη διχοτόμο της γωνίας
είναι και στη διχοτόμο της γωνίας 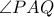 , οπότε από τις δύο σχέσεις το
, οπότε από τις δύο σχέσεις το  είναι το παράκεντρο του
είναι το παράκεντρο του  .
.Σιλουανός Μπραζιτίκος
- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: EGMO 2019
Αν δει κανείς το  από τη σωστή οπτική γωνία η λύση είναι απλή και σύντομη. Μόνο που μου πήρε αρκετή ώρα να τη βρω...
από τη σωστή οπτική γωνία η λύση είναι απλή και σύντομη. Μόνο που μου πήρε αρκετή ώρα να τη βρω...
Υποθέτω ότι δεν υπάρχει μπλε ετικέτα με τιμή πολλαπλάσιο του .
.
Για κάθε χορδή ορίζω το διάνυσμα όπου
όπου  είναι το πλήθος των τμημάτων με άθροισμα άκρων
είναι το πλήθος των τμημάτων με άθροισμα άκρων 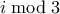 . Αν τα άκρα της χορδής είναι ίδια, ισχυρίζομαι ότι
. Αν τα άκρα της χορδής είναι ίδια, ισχυρίζομαι ότι  . Αν τα άκρα της χορδής έχουν διαφορετικούς αριθμούς (δηλαδή
. Αν τα άκρα της χορδής έχουν διαφορετικούς αριθμούς (δηλαδή  και
και  ) ισχυρίζομαι ότι
) ισχυρίζομαι ότι  . Αυτό είναι άμεσο αν η χορδή δεν έχει σημαδεμένο εσωτερικό σημείο (δηλαδή τα άκρα της είναι
. Αυτό είναι άμεσο αν η χορδή δεν έχει σημαδεμένο εσωτερικό σημείο (δηλαδή τα άκρα της είναι  και
και  ) ή αν έχει ένα σημαδεμένο εσωτερικό σημείο με αριθμό
) ή αν έχει ένα σημαδεμένο εσωτερικό σημείο με αριθμό  . (Δηλαδή έχουμε τις περιπτώσεις όπου κατά σειρά τα σημεία έχουν τους αριθμούς
. (Δηλαδή έχουμε τις περιπτώσεις όπου κατά σειρά τα σημεία έχουν τους αριθμούς  ή
ή  ή
ή  ή
ή  .) Για το επαγωγικό βήμα, βρίσκω ένα εσωτερικό σημείο ίσο με
.) Για το επαγωγικό βήμα, βρίσκω ένα εσωτερικό σημείο ίσο με  ή
ή  (δεν μπορεί να είναι όλα
(δεν μπορεί να είναι όλα  ) και σπάω τη χορδή σε δύο χορδές στις οποίες ισχύει το ζητούμενο από την επαγωγική υπόθεση. Ένας απλός έλεγχος περιπτώσεων δείχνει ότι το ζητούμενο ισχύει και για ολόκληρη τη χορδή.
) και σπάω τη χορδή σε δύο χορδές στις οποίες ισχύει το ζητούμενο από την επαγωγική υπόθεση. Ένας απλός έλεγχος περιπτώσεων δείχνει ότι το ζητούμενο ισχύει και για ολόκληρη τη χορδή.
Προσθέτω τώρα όλα τα διανύσματα όλων τον χορδών. Θα έχω περιττό πλήθος από χορδές με διαφορετικούς αριθμούς. Άρα αν το άθροισμα είναι τότε θα έχω
τότε θα έχω  . Όμως κοιτάζοντας τις κίτρινες ετικέτες πρέπει
. Όμως κοιτάζοντας τις κίτρινες ετικέτες πρέπει  ή
ή  , άτοπο.
, άτοπο.
 από τη σωστή οπτική γωνία η λύση είναι απλή και σύντομη. Μόνο που μου πήρε αρκετή ώρα να τη βρω...
από τη σωστή οπτική γωνία η λύση είναι απλή και σύντομη. Μόνο που μου πήρε αρκετή ώρα να τη βρω...Υποθέτω ότι δεν υπάρχει μπλε ετικέτα με τιμή πολλαπλάσιο του
 .
.Για κάθε χορδή ορίζω το διάνυσμα
 όπου
όπου  είναι το πλήθος των τμημάτων με άθροισμα άκρων
είναι το πλήθος των τμημάτων με άθροισμα άκρων 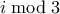 . Αν τα άκρα της χορδής είναι ίδια, ισχυρίζομαι ότι
. Αν τα άκρα της χορδής είναι ίδια, ισχυρίζομαι ότι  . Αν τα άκρα της χορδής έχουν διαφορετικούς αριθμούς (δηλαδή
. Αν τα άκρα της χορδής έχουν διαφορετικούς αριθμούς (δηλαδή  και
και  ) ισχυρίζομαι ότι
) ισχυρίζομαι ότι  . Αυτό είναι άμεσο αν η χορδή δεν έχει σημαδεμένο εσωτερικό σημείο (δηλαδή τα άκρα της είναι
. Αυτό είναι άμεσο αν η χορδή δεν έχει σημαδεμένο εσωτερικό σημείο (δηλαδή τα άκρα της είναι  και
και  ) ή αν έχει ένα σημαδεμένο εσωτερικό σημείο με αριθμό
) ή αν έχει ένα σημαδεμένο εσωτερικό σημείο με αριθμό  . (Δηλαδή έχουμε τις περιπτώσεις όπου κατά σειρά τα σημεία έχουν τους αριθμούς
. (Δηλαδή έχουμε τις περιπτώσεις όπου κατά σειρά τα σημεία έχουν τους αριθμούς  ή
ή  ή
ή  ή
ή  .) Για το επαγωγικό βήμα, βρίσκω ένα εσωτερικό σημείο ίσο με
.) Για το επαγωγικό βήμα, βρίσκω ένα εσωτερικό σημείο ίσο με  ή
ή  (δεν μπορεί να είναι όλα
(δεν μπορεί να είναι όλα  ) και σπάω τη χορδή σε δύο χορδές στις οποίες ισχύει το ζητούμενο από την επαγωγική υπόθεση. Ένας απλός έλεγχος περιπτώσεων δείχνει ότι το ζητούμενο ισχύει και για ολόκληρη τη χορδή.
) και σπάω τη χορδή σε δύο χορδές στις οποίες ισχύει το ζητούμενο από την επαγωγική υπόθεση. Ένας απλός έλεγχος περιπτώσεων δείχνει ότι το ζητούμενο ισχύει και για ολόκληρη τη χορδή.Προσθέτω τώρα όλα τα διανύσματα όλων τον χορδών. Θα έχω περιττό πλήθος από χορδές με διαφορετικούς αριθμούς. Άρα αν το άθροισμα είναι
 τότε θα έχω
τότε θα έχω  . Όμως κοιτάζοντας τις κίτρινες ετικέτες πρέπει
. Όμως κοιτάζοντας τις κίτρινες ετικέτες πρέπει  ή
ή  , άτοπο.
, άτοπο.- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: EGMO 2019
Βγήκαν τα τελικά αποτελέσματα.
Η Κύπρος είχε ένα χάλκινο με την Ειρήνη Ιωάννου. (Το πρώτο μας σε EGMO.)
Η Ελλάδα είχε δύο χάλκινα με τις Ειρήνη Μηλιώρη και Άρτεμις Σάββα. Είχε επίσης δύο εύφημες μνείες με τις Κωνσταντίνα Ρασβάνη και Δανάη Αβδελά.
Συγχαρητήρια σε όλες!
Η Κύπρος είχε ένα χάλκινο με την Ειρήνη Ιωάννου. (Το πρώτο μας σε EGMO.)
Η Ελλάδα είχε δύο χάλκινα με τις Ειρήνη Μηλιώρη και Άρτεμις Σάββα. Είχε επίσης δύο εύφημες μνείες με τις Κωνσταντίνα Ρασβάνη και Δανάη Αβδελά.
Συγχαρητήρια σε όλες!
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
- cretanman
- Διαχειριστής
- Δημοσιεύσεις: 4097
- Εγγραφή: Πέμ Δεκ 18, 2008 12:35 pm
- Τοποθεσία: Ηράκλειο Κρήτης
- Επικοινωνία:
Re: EGMO 2019
Συγχαρητήρια σε όλα τα κορίτσια της Ελληνικής και Κυπριακής αποστολής για τη συμμετοχή και τις διακρίσεις τους αλλά και στους αρχηγούς/υπαρχηγούς, που πάλεψαν για το καλύτερο δυνατό αποτέλεσμα!
Αλέξανδρος
Αλέξανδρος
Αλέξανδρος Συγκελάκης
-
christinat
- Δημοσιεύσεις: 50
- Εγγραφή: Κυρ Δεκ 23, 2018 11:26 pm
- Τοποθεσία: Αθήνα
Re: EGMO 2019
Πολλά συγχαρητήρια στα κορίτσια!!!
Δινω μια άλλη λυση για το πρόβλημα 1
 (1)
(1)
Ισχύει ακόμη ότι
 (2)
(2)
 (3)
(3)
Από τις σχέσεις (1)-(2)-(3) έχουμε:

Επίσης (4)
(4)
Από την (4) και την παίρνουνε
παίρνουνε




Όποτε:



Άρα (5)
(5)
Αν για να ισχύει η σχεση (5) πρέπει
για να ισχύει η σχεση (5) πρέπει

Η ισότητα ισχύει για
ή (6)
(6)
Αν τοτε από την εξίσωση
τοτε από την εξίσωση  προκύπτει ότι
προκύπτει ότι 
Πρέπει ή
ή 
Εσυ οι δυνατές τριάδες σε αυτήν την περίπτωση είναι (7)
(7)
Αντίστοιχα αν :
:
 (8)
(8)
Αν :
:
 ή
ή (9)
(9)
Οι σχέσεις (6)-(7)-(8)-(9) δίνουν τις τριάδες που ικανοποιούν τις εξισώσεις της άσκησης
Δινω μια άλλη λυση για το πρόβλημα 1
 (1)
(1)Ισχύει ακόμη ότι
 (2)
(2) (3)
(3)Από τις σχέσεις (1)-(2)-(3) έχουμε:

Επίσης
 (4)
(4)Από την (4) και την
 παίρνουνε
παίρνουνε 



Όποτε:



Άρα
 (5)
(5)Αν
 για να ισχύει η σχεση (5) πρέπει
για να ισχύει η σχεση (5) πρέπει 
Η ισότητα ισχύει για

ή
 (6)
(6)Αν
 τοτε από την εξίσωση
τοτε από την εξίσωση  προκύπτει ότι
προκύπτει ότι 
Πρέπει
 ή
ή 
Εσυ οι δυνατές τριάδες σε αυτήν την περίπτωση είναι
 (7)
(7)Αντίστοιχα αν
 :
: (8)
(8)Αν
 :
: ή
ή (9)
(9)Οι σχέσεις (6)-(7)-(8)-(9) δίνουν τις τριάδες που ικανοποιούν τις εξισώσεις της άσκησης
Τσούρα Χριστίνα
-
christinat
- Δημοσιεύσεις: 50
- Εγγραφή: Κυρ Δεκ 23, 2018 11:26 pm
- Τοποθεσία: Αθήνα
Re: EGMO 2019
Βάζω μια λυση και για το 4
Έστω ,
, ,
, οι προβολές από το
οι προβολές από το  στις πλευρές του τριγώνου
στις πλευρές του τριγώνου 
Το είναι ο ριζικός άξονας των
είναι ο ριζικός άξονας των  και
και 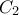
Όποτε



Από το θεώρημα του έχουμε:
έχουμε:

Οι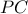 και
και  διχοτομουν τις γωνιές
διχοτομουν τις γωνιές
 και
και 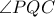 αντίστοιχα
αντίστοιχα
Όποτε και
και 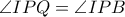
Άρα παράκεντρο(από το Α) του
παράκεντρο(από το Α) του 
Το εγκεντρο του
του  είναι το παρακεντρο του
είναι το παρακεντρο του  ,σχεση από την οποία προκύπτει το ζητούμενο
,σχεση από την οποία προκύπτει το ζητούμενο
Έστω
 ,
, ,
, οι προβολές από το
οι προβολές από το  στις πλευρές του τριγώνου
στις πλευρές του τριγώνου 
Το
 είναι ο ριζικός άξονας των
είναι ο ριζικός άξονας των  και
και 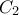
Όποτε




Από το θεώρημα του
 έχουμε:
έχουμε:
Οι
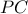 και
και  διχοτομουν τις γωνιές
διχοτομουν τις γωνιές  και
και 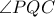 αντίστοιχα
αντίστοιχα Όποτε
 και
και 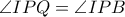
Άρα
 παράκεντρο(από το Α) του
παράκεντρο(από το Α) του 
Το εγκεντρο
 του
του  είναι το παρακεντρο του
είναι το παρακεντρο του  ,σχεση από την οποία προκύπτει το ζητούμενο
,σχεση από την οποία προκύπτει το ζητούμενοΤσούρα Χριστίνα
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 15 επισκέπτες
