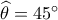 .
.Δεκτές όλες οι λύσεις αλλά λόγω σαρακοστής να δούμε λύση χωρίς τριγωνομετρία .
Συντονιστής: Γιώργος Ρίζος
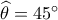 .
. του επιπέδου, ώστε
του επιπέδου, ώστε  ,
, 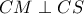 και το
και το  να είναι σε διαφορετικό ημιεπίπεδο της
να είναι σε διαφορετικό ημιεπίπεδο της  από το
από το  .
. .
. και άρα
και άρα  .
. , και αφού
, και αφού  , τα ορθογώνια τρίγωνα
, τα ορθογώνια τρίγωνα  είναι ίσα.
είναι ίσα. .
. , επομένως τα τρίγωνα
, επομένως τα τρίγωνα 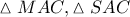 έχουν :
έχουν :
 κοινή
κοινή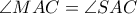 .
.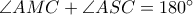 .
.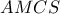 να είναι εγγράψιμο, δηλαδή
να είναι εγγράψιμο, δηλαδή  , προφανώς άτοπο.
, προφανώς άτοπο. .
.Σε τέτοια ηλικία , τόσες "στροφές" μόνο θαυμασμό προκαλούνΟρέστης Λιγνός έγραψε: ↑Τετ Μαρ 13, 2019 2:17 pmΓεια σας κύριε Νίκο και Καλή Σαρακοστή!
Παίρνω σημείοτου επιπέδου, ώστε
,
και το
να είναι σε διαφορετικό ημιεπίπεδο της
από το
.
Φέρνω,.
Είναι, (εύκολο)και άρα
.
Επίσης, έχω, και αφού
, τα ορθογώνια τρίγωνα
είναι ίσα.
Έτσι,.
Είναι,, επομένως τα τρίγωνα
έχουν :
i)
ii)κοινή
iii).
Άρα, από το έμμεσο κριτήριο ισότητας τριγώνων (*), προκύπτει ότι είναι ίσα, ή ότι.
Αν ισχύει το δεύτερο, πρέπει τονα είναι εγγράψιμο, δηλαδή
, προφανώς άτοπο.
Άρα, τα προαναφερθέντα τρίγωνα είναι ίσα, συνεπώς.
(*) Για το έμμεσο κριτήριο δείτε εδώ (η απόδειξη του γίνεται και με Ν.Ημιτόνων)
Με Πυθαγόρειο εύκολα
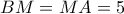 και
και 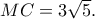 Με 1ο θεώρημα διαμέσων:
Με 1ο θεώρημα διαμέσων: 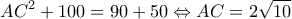

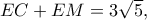 θα είναι
θα είναι  οπότε το
οπότε το  είναι ορθογώνιο και ισοσκελές και
είναι ορθογώνιο και ισοσκελές και 
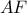 και τις διαμέσους
και τις διαμέσους  . Ευκολα από π.θ. έχουμε ότι:
. Ευκολα από π.θ. έχουμε ότι:  .
. 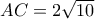
 είναι βαρύκεντρο του
είναι βαρύκεντρο του  οπότε
οπότε  . Τότε το
. Τότε το 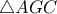 είναι ορθογώνιο και ισοσκελές, οπότε
είναι ορθογώνιο και ισοσκελές, οπότε 
Αυτή είναι η λύση μου αλλά χωρίς υπολογισμούς αφού τα τρίγωνα :
 είναι όμοια άρα και ισογώνια και το
είναι όμοια άρα και ισογώνια και το  είναι ισοσκελές τραπέζιο .
είναι ισοσκελές τραπέζιο .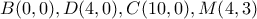 , οπότε
, οπότε  , άρα
, άρα 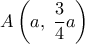 .
. μέσο του
μέσο του  είναι
είναι  , οπότε
, οπότε 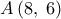 .
. .
.  στην
στην  , έχει εξίσωση
, έχει εξίσωση 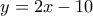 και την τέμνει στο
και την τέμνει στο  .
. 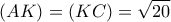 οπότε το
οπότε το 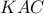 είναι ορθογώνιο και ισοσκελές, άρα
είναι ορθογώνιο και ισοσκελές, άρα  .
.  και
και 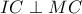 . Βρίσκουμε
. Βρίσκουμε 
 άρα
άρα  διχοτόμος της
διχοτόμος της 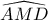 .
.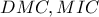 είναι όμοια με συνέπειες:
είναι όμοια με συνέπειες: 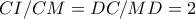 και
και 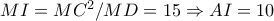 .
. άρα
άρα  διχοτόμος της ορθής
διχοτόμος της ορθής 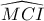 οπότε
οπότε  . Φιλικά, Γιώργος.
. Φιλικά, Γιώργος.Καλημέρα από το σχολείο!Προεκτείνουμε την
 κατά
κατά  και προφανώς
και προφανώς 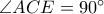
 και από αντίστροφο θεωρήματος διχοτόμου, το ζητούμενο έπεται.
και από αντίστροφο θεωρήματος διχοτόμου, το ζητούμενο έπεται.Κατασκευάζω το ορθογώνιο
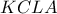
 είναι το μέσο της
είναι το μέσο της  τότε
τότε 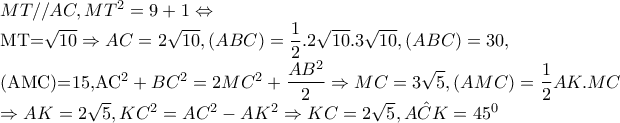
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 16 επισκέπτες