 και
και  τέμνονται στα σημεία
τέμνονται στα σημεία  και
και  . Η εφαπτομένη του πρώτου κύκλου, που άγεται στο σημείο
. Η εφαπτομένη του πρώτου κύκλου, που άγεται στο σημείο  , τέμνει
, τέμνειτην εφαπτομένη στο
 του δεύτερου κύκλου, στο σημείο
του δεύτερου κύκλου, στο σημείο  . Να αποδείξετε ότι οι γωνίες
. Να αποδείξετε ότι οι γωνίες  και
και  έχουν κοινή διχοτόμο.
έχουν κοινή διχοτόμο.Συντονιστές: vittasko, silouan, Doloros
 και
και  τέμνονται στα σημεία
τέμνονται στα σημεία  και
και  . Η εφαπτομένη του πρώτου κύκλου, που άγεται στο σημείο
. Η εφαπτομένη του πρώτου κύκλου, που άγεται στο σημείο  , τέμνει
, τέμνει του δεύτερου κύκλου, στο σημείο
του δεύτερου κύκλου, στο σημείο  . Να αποδείξετε ότι οι γωνίες
. Να αποδείξετε ότι οι γωνίες  και
και  έχουν κοινή διχοτόμο.
έχουν κοινή διχοτόμο.Ας δούμε μια λύση με στοιχειώδη μέσα στο όμορφο πρόβλημα του Γιάννηgiannimani έγραψε: ↑Σάβ Φεβ 09, 2019 6:39 pmΔύο άνισοι κύκλοι με κέντρακαι
τέμνονται στα σημεία
και
. Η εφαπτομένη του πρώτου κύκλου, που άγεται στο σημείο
, τέμνει
την εφαπτομένη στοτου δεύτερου κύκλου, στο σημείο
. Να αποδείξετε ότι οι γωνίες
και
έχουν κοινή διχοτόμο.sm_bis.png
 . Τότε έχουμε:
. Τότε έχουμε:  (υπό χορδής και εφαπτομένης – αντίστοιχη εγγεγραμμένη στον κύκλο
(υπό χορδής και εφαπτομένης – αντίστοιχη εγγεγραμμένη στον κύκλο  ) οπότε επειδή τα τρίγωνα
) οπότε επειδή τα τρίγωνα  μοιράζονται και τη γωνία
μοιράζονται και τη γωνία  θα είναι όμοια , άρα
θα είναι όμοια , άρα  Επίσης
Επίσης 


 έχοντας τις γωνίες των «κορυφών» τους ίσες θα είναι όμοια οπότε
έχοντας τις γωνίες των «κορυφών» τους ίσες θα είναι όμοια οπότε 
 . Από την
. Από την 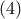 προκύπτει ότι οι αντίστοιχες κάθετες πλευρές των ορθογωνίων (στις κορυφές
προκύπτει ότι οι αντίστοιχες κάθετες πλευρές των ορθογωνίων (στις κορυφές  από τις επαφές) τριγώνων
από τις επαφές) τριγώνων  αντίστοιχα είναι ανάλογες , οπότε αυτά είναι όμοια και συνεπώς
αντίστοιχα είναι ανάλογες , οπότε αυτά είναι όμοια και συνεπώς  οπότε οι γωνίες
οπότε οι γωνίες  έχουν κοινή διχοτόμο και το ζητούμενο έχει αποδειχθεί.
έχουν κοινή διχοτόμο και το ζητούμενο έχει αποδειχθεί.Ας δούμε και μια διαφορετική αντιμετώπιση που "πιθανόν" να δικαιολογεί και το φάκελο ...giannimani έγραψε: ↑Σάβ Φεβ 09, 2019 6:39 pmΔύο άνισοι κύκλοι με κέντρακαι
τέμνονται στα σημεία
και
. Η εφαπτομένη του πρώτου κύκλου, που άγεται στο σημείο
, τέμνει
την εφαπτομένη στοτου δεύτερου κύκλου, στο σημείο
. Να αποδείξετε ότι οι γωνίες
και
έχουν κοινή διχοτόμο.sm_bis.png
 τα δεύτερα (εκτός των
τα δεύτερα (εκτός των  εφαπτομενικά τμήματα των κύκλων
εφαπτομενικά τμήματα των κύκλων  αντίστοιχα και ας είναι
αντίστοιχα και ας είναι 

 τις πολικές του
τις πολικές του  ως προς τους κύκλους
ως προς τους κύκλους  αντίστοιχα προκύπτει ότι οι σειρές
αντίστοιχα προκύπτει ότι οι σειρές  είναι αρμονικές άρα έχουν ίσους διπλούς λόγους , δηλαδή
είναι αρμονικές άρα έχουν ίσους διπλούς λόγους , δηλαδή  Με
Με 


 ομοκυκλικά , οπότε
ομοκυκλικά , οπότε  άρα τα ισοσκελή τρίγωνα (από τα εφαπτομενικά τμήματα …)
άρα τα ισοσκελή τρίγωνα (από τα εφαπτομενικά τμήματα …)  είναι όμοια και συνεπώς
είναι όμοια και συνεπώς 
 και το ζητούμενο έπεται (όπως στην προηγούμενη ανάρτηση)
και το ζητούμενο έπεται (όπως στην προηγούμενη ανάρτηση) η οποία τέμνει την ευθεία
η οποία τέμνει την ευθεία  στο σημείο
στο σημείο  . Θα αποδείξουμε ότι η
. Θα αποδείξουμε ότι η  είναι διχοτόμος και της γωνίας
είναι διχοτόμος και της γωνίας  .
.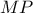 και
και  τέμνονται στο σημείο
τέμνονται στο σημείο  . Τότε, εφόσον
. Τότε, εφόσον  , τα σημεία
, τα σημεία  ,
,  ,
,  και
και  ανήκουν σε κύκλο
ανήκουν σε κύκλο  διαμέτρου
διαμέτρου  . Το κέντρο
. Το κέντρο  αυτού του κύκλου ανήκει στην ευθεία
αυτού του κύκλου ανήκει στην ευθεία  (εφόσον η τελευταία είναι μεσοκάθετος της κοινής χορδής
(εφόσον η τελευταία είναι μεσοκάθετος της κοινής χορδής  των κύκλων της υπόθεσης), η οποία διέρχεται επίσης από το μέσο του τόξου
των κύκλων της υπόθεσης), η οποία διέρχεται επίσης από το μέσο του τόξου  του κύκλου
του κύκλου  , που είναι το σημείο
, που είναι το σημείο  .
.  το δεύτερο κοινό σημείο της
το δεύτερο κοινό σημείο της  με τον κύκλο
με τον κύκλο  . Η
. Η  διάμετρος του
διάμετρος του  , οπότε
, οπότε  .
. διχοτόμος της γωνίας
διχοτόμος της γωνίας  , αρκεί
, αρκεί 
 .
. και
και  είναι εγγράψιμα. Πράγματι,
είναι εγγράψιμα. Πράγματι, .
.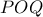 είναι αντίστοιχη επίκεντρη της γωνίας
είναι αντίστοιχη επίκεντρη της γωνίας  , και η
, και η  διχοτόμος της
διχοτόμος της 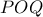 ).
). .
. και
και  το μέσο του ευθύγραμμου τμήματος
το μέσο του ευθύγραμμου τμήματος  , τότε
, τότε  .
. ,
,  ,
,  και
και  , με αυτή τη σειρά, που ανήκουν σε μία ευθεία
, με αυτή τη σειρά, που ανήκουν σε μία ευθεία  .
.  .
. είναι εσωτερική διχοτόμος της
είναι εσωτερική διχοτόμος της  , όπου
, όπου  .
. , όπου
, όπου  .
. .Όπως είδαμε και παραπάνω είναι
.Όπως είδαμε και παραπάνω είναι  .Θεωρούμε σύνθεση αντιστροφής κέντρου
.Θεωρούμε σύνθεση αντιστροφής κέντρου  και ακτίνας
και ακτίνας  και συμμετρίας ως προς τη διχοτόμο της
και συμμετρίας ως προς τη διχοτόμο της  .Τα
.Τα  ανταλλάσσονται,ενώ και
ανταλλάσσονται,ενώ και  ανταλλάσονται,αφού
ανταλλάσονται,αφού  από Θαλή,δηλαδή
από Θαλή,δηλαδή  .Άρα ο
.Άρα ο  πάει στον
πάει στον  κι αντίστροφα.Αν δούμε λίγο τον κύκλο που προκύπτει από αυτή τη σύνθεση μετασχηματισμών πριν όμως τη συμμετρία,αυτός είναι ο αντίστροφος του
κι αντίστροφα.Αν δούμε λίγο τον κύκλο που προκύπτει από αυτή τη σύνθεση μετασχηματισμών πριν όμως τη συμμετρία,αυτός είναι ο αντίστροφος του  .Άρα,το κέντρο του κύκλου αυτού βρίσκεται πάνω στην
.Άρα,το κέντρο του κύκλου αυτού βρίσκεται πάνω στην  ,αφού το
,αφού το  κέντρο του αρχικού κύκλου (γνωστή πρόταση).Άρα,τα
κέντρο του αρχικού κύκλου (γνωστή πρόταση).Άρα,τα  ,με
,με  το κέντρο του αντίστροφου του
το κέντρο του αντίστροφου του 
 θα πέσει κάπου στη
θα πέσει κάπου στη  από όπου έπεται η ισογωνιότητα..
από όπου έπεται η ισογωνιότητα..Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες