Διαγωνισμός EMC 2018
Συντονιστές: cretanman, ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ, socrates
-
jason.prod
- Δημοσιεύσεις: 141
- Εγγραφή: Τρί Φεβ 25, 2014 5:29 pm
Διαγωνισμός EMC 2018
Καλησπέρα σε όλα τα μέλη του forum που ασχολούνται με τους μαθηματικούς διαγωνισμούς.
Φέτος είναι η 7η χρονιά που διοργανώνεται το European Mathematical Cup, ένας διαγωνισμός που απευθύνεται σε παιδιά γυμνασίου και λυκείου. Είναι ένας διαγωνισμός που διοργανώνεται σε δύο επίπεδα (juniors, seniors) και επιπέδου μάλλον ανάλογου των αντίστοιχων βαλκανιάδων. Πρόκειται για μια προπόνηση πολύ καλού επιπέδου για όσους προετοιμάζονται για τους αντίστοιχους διαγωνισμούς. Όποιος το θέλει μπορεί να συμμετάσχει σε αυτόν τον διαγωνισμό.
Για περισσότερες πληροφορίες, μπορείτε να επισκεφτείτε το site του διαγωνισμού (http://emc.mnm.hr/) ή αν θέλετε να δείτε τα παλιά θέματα, μπορείτε να επισκεφτείτε το αντίστοιχο θέμα στο AOPS (https://artofproblemsolving.com/communi ... atical_cup).
Όποιος θέλει περισσότερες πληροφορίες ή να δηλώσει συμμετοχή, μπορεί να μου στείλει e-mail στη διεύθυνση kyprianos@prodromidis.com ή να μου στείλει ΠΜ στο mathematica ή στο facebook (Jason Prodromidis). Στη δήλωση συμμετοχής, θα πρέπει να υπάρχουν οπωσδήποτε:
1) Όνομα του διαγωνιζόμενου, και στα ελληνικά και στα αγγλικά.
2) Ηλικία, Τάξη.
3) Κατηγορία με την οποία θέλει να συμμετέχει στο διαγωνισμό.
Ο διαγωνισμός φέτος διεξάγεται από 8 ως 16 Δεκεμβρίου 2018. Επειδή υπάρχει σχετική ελευθερία, όποιος θέλει, κατά τη δήλωση συμμετοχής, μπορεί να δηλώσει και προτίμηση για συγκεκριμένη ημερομηνία διεξαγωγής του διαγωνισμού . Οι μαθητές που θα δηλώσουν συμμετοχή, θα ενημερωθούν για την ημερομηνία, την ώρα αλλά και τον τόπο της εξέτασης έγκαιρα. Η ημερομηνία αναμένεται να είναι μία από τα δύο Σάββατα εντός της προθεσμίας.
Φέτος είναι η 7η χρονιά που διοργανώνεται το European Mathematical Cup, ένας διαγωνισμός που απευθύνεται σε παιδιά γυμνασίου και λυκείου. Είναι ένας διαγωνισμός που διοργανώνεται σε δύο επίπεδα (juniors, seniors) και επιπέδου μάλλον ανάλογου των αντίστοιχων βαλκανιάδων. Πρόκειται για μια προπόνηση πολύ καλού επιπέδου για όσους προετοιμάζονται για τους αντίστοιχους διαγωνισμούς. Όποιος το θέλει μπορεί να συμμετάσχει σε αυτόν τον διαγωνισμό.
Για περισσότερες πληροφορίες, μπορείτε να επισκεφτείτε το site του διαγωνισμού (http://emc.mnm.hr/) ή αν θέλετε να δείτε τα παλιά θέματα, μπορείτε να επισκεφτείτε το αντίστοιχο θέμα στο AOPS (https://artofproblemsolving.com/communi ... atical_cup).
Όποιος θέλει περισσότερες πληροφορίες ή να δηλώσει συμμετοχή, μπορεί να μου στείλει e-mail στη διεύθυνση kyprianos@prodromidis.com ή να μου στείλει ΠΜ στο mathematica ή στο facebook (Jason Prodromidis). Στη δήλωση συμμετοχής, θα πρέπει να υπάρχουν οπωσδήποτε:
1) Όνομα του διαγωνιζόμενου, και στα ελληνικά και στα αγγλικά.
2) Ηλικία, Τάξη.
3) Κατηγορία με την οποία θέλει να συμμετέχει στο διαγωνισμό.
Ο διαγωνισμός φέτος διεξάγεται από 8 ως 16 Δεκεμβρίου 2018. Επειδή υπάρχει σχετική ελευθερία, όποιος θέλει, κατά τη δήλωση συμμετοχής, μπορεί να δηλώσει και προτίμηση για συγκεκριμένη ημερομηνία διεξαγωγής του διαγωνισμού . Οι μαθητές που θα δηλώσουν συμμετοχή, θα ενημερωθούν για την ημερομηνία, την ώρα αλλά και τον τόπο της εξέτασης έγκαιρα. Η ημερομηνία αναμένεται να είναι μία από τα δύο Σάββατα εντός της προθεσμίας.
Προδρομίδης Κυπριανός-Ιάσων
Λέξεις Κλειδιά:
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
Re: Διαγωνισμός EMC 2018
Θα συμμετάσχουμε και εμείς! Εύχομαι καλή επιτυχία σε όλα τα παιδιά που θα διαγωνιστούν.
Υ.γ: Η ημερομηνία του διαγωνισμού είναι τελικά 15 Δεκέμβρη! Το εξεταστικό κέντρο θα είναι το πρότυπο ΓΕΛ Αναβρύτων και ο διαγωνισμός θα διαρκέσει 4 ώρες από τις 9 μέχρι την 1
Υ.γ: Η ημερομηνία του διαγωνισμού είναι τελικά 15 Δεκέμβρη! Το εξεταστικό κέντρο θα είναι το πρότυπο ΓΕΛ Αναβρύτων και ο διαγωνισμός θα διαρκέσει 4 ώρες από τις 9 μέχρι την 1
- ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ
- Δημοσιεύσεις: 921
- Εγγραφή: Πέμ Νοέμ 22, 2018 9:43 pm
Re: Διαγωνισμός EMC 2018
Μιας και έχει λήξει ο διαγωνισμός επιτρέπεται να παραθέσουμε τα θέματα για να τα συζητήσουμε ή πρέπει να περιμένουμε λίγο ;
-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
Re: Διαγωνισμός EMC 2018
Ζητήθηκε από την επιτροπή να μην δημοσιευτούν πριν τις 22 Δεκέμβρη. Θα τα ανεβάσω τότε για να συζητηθούν! Σύμφωνα με τα λεγόμενα των συμμετεχόντων ( και δική μου γνώμη ) τα θέματα ήταν δύσκολα αλλά πάρα πολύ ωραία! 
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: Διαγωνισμός EMC 2018
Τα θέματα των Juniors είναι πιό κάτω.
τελευταία επεξεργασία από Ορέστης Λιγνός σε Τρί Δεκ 25, 2018 7:20 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Κερδίζουμε ό,τι τολμούμε!
- ΘΕΟΔΟΣΙΟΣ ΦΩΤΙΑΔΗΣ
- Δημοσιεύσεις: 141
- Εγγραφή: Πέμ Νοέμ 22, 2018 11:47 pm
Re: Διαγωνισμός EMC 2018
Χαίρετε και καλά Χριστούγεννα 
Παραθέτω τα θέματα των Juniors σε Latex:
1. Αν οι μη μηδενικοί πραγματικοί αριθμοί ικανοποιούν τις σχέσεις
ικανοποιούν τις σχέσεις



να αποδειχθεί οτι δύο απο αυτούς είναι ίσοι.
2. Να βρεθούν όλα τα ζεύγη θετικών ακεραίων, που ικανοποιούν τη σχέση
θετικών ακεραίων, που ικανοποιούν τη σχέση 
3. Δίνεται τρίγωνο με
με  με ορθόκεντρο
με ορθόκεντρο  . Ο κύκλος με κίντρο
. Ο κύκλος με κίντρο  και ακτίνα
και ακτίνα  τέμνει τον περιγεγραμμένο κύκλο του
τέμνει τον περιγεγραμμένο κύκλο του  στο
στο  , ενώ ο κύκλος κέντρου
, ενώ ο κύκλος κέντρου  και ακτίνας
και ακτίνας  τέμνει την
τέμνει την  στο
στο  . Η από το
. Η από το  παράλληλη στην
παράλληλη στην  τέμνει την
τέμνει την  στο
στο  , ενώ
, ενώ  είναι το ίχνος της κάθετης από το
είναι το ίχνος της κάθετης από το  προς την
προς την  . Να αποδειχθεί ότι το μέσο την
. Να αποδειχθεί ότι το μέσο την  , το μέσο
, το μέσο  της
της  και το
και το  είναι συνευθειακά.
είναι συνευθειακά.
4. Ο Γιάννης και ο Γιώργος έχουν μπροστά τους ποτήρια στη σειρά. Ο Γιάννης επιλέγει, χωρίς ο Γιώργος να βλέπει, δύο ποτήρια. Κάτω απο το ένα ανοίγει μια τρύπα και κάτω από το άλλο βάζει ένα μπαλάκι. Μία κίνηση αποτελείται απο την εναλλαγή δύο διαδοχικών ποτηριών της σειράς.
ποτήρια στη σειρά. Ο Γιάννης επιλέγει, χωρίς ο Γιώργος να βλέπει, δύο ποτήρια. Κάτω απο το ένα ανοίγει μια τρύπα και κάτω από το άλλο βάζει ένα μπαλάκι. Μία κίνηση αποτελείται απο την εναλλαγή δύο διαδοχικών ποτηριών της σειράς.
Η αποστολή του Γιώργου είναι η εξής: Πρέπει να δώσει μια σειρά από πεπερασμένες κινήσεις στο Γιάννη, τις οποίες ο Γιάννης εκτελεί, οι οποίες θα οδηγήσουν σίγουρα στο να πέσει το μπαλάκι μέσα στην τρύπα. Να βρεθεί ο ελάχιστος αριθμός από κινήσεις τις οποίες πρέπει να δώσει ο Γιώργος στο Γιάννη, ώστε να είναι σίγουρος ότι θα πετύχει την αποστολή του.
Παραθέτω τα θέματα των Juniors σε Latex:
1. Αν οι μη μηδενικοί πραγματικοί αριθμοί
 ικανοποιούν τις σχέσεις
ικανοποιούν τις σχέσεις 


να αποδειχθεί οτι δύο απο αυτούς είναι ίσοι.
2. Να βρεθούν όλα τα ζεύγη
 θετικών ακεραίων, που ικανοποιούν τη σχέση
θετικών ακεραίων, που ικανοποιούν τη σχέση 
3. Δίνεται τρίγωνο
 με
με  με ορθόκεντρο
με ορθόκεντρο  . Ο κύκλος με κίντρο
. Ο κύκλος με κίντρο  και ακτίνα
και ακτίνα  τέμνει τον περιγεγραμμένο κύκλο του
τέμνει τον περιγεγραμμένο κύκλο του  στο
στο  , ενώ ο κύκλος κέντρου
, ενώ ο κύκλος κέντρου  και ακτίνας
και ακτίνας  τέμνει την
τέμνει την  στο
στο  . Η από το
. Η από το  παράλληλη στην
παράλληλη στην  τέμνει την
τέμνει την  στο
στο  , ενώ
, ενώ  είναι το ίχνος της κάθετης από το
είναι το ίχνος της κάθετης από το  προς την
προς την  . Να αποδειχθεί ότι το μέσο την
. Να αποδειχθεί ότι το μέσο την  , το μέσο
, το μέσο  της
της  και το
και το  είναι συνευθειακά.
είναι συνευθειακά.4. Ο Γιάννης και ο Γιώργος έχουν μπροστά τους
 ποτήρια στη σειρά. Ο Γιάννης επιλέγει, χωρίς ο Γιώργος να βλέπει, δύο ποτήρια. Κάτω απο το ένα ανοίγει μια τρύπα και κάτω από το άλλο βάζει ένα μπαλάκι. Μία κίνηση αποτελείται απο την εναλλαγή δύο διαδοχικών ποτηριών της σειράς.
ποτήρια στη σειρά. Ο Γιάννης επιλέγει, χωρίς ο Γιώργος να βλέπει, δύο ποτήρια. Κάτω απο το ένα ανοίγει μια τρύπα και κάτω από το άλλο βάζει ένα μπαλάκι. Μία κίνηση αποτελείται απο την εναλλαγή δύο διαδοχικών ποτηριών της σειράς.Η αποστολή του Γιώργου είναι η εξής: Πρέπει να δώσει μια σειρά από πεπερασμένες κινήσεις στο Γιάννη, τις οποίες ο Γιάννης εκτελεί, οι οποίες θα οδηγήσουν σίγουρα στο να πέσει το μπαλάκι μέσα στην τρύπα. Να βρεθεί ο ελάχιστος αριθμός από κινήσεις τις οποίες πρέπει να δώσει ο Γιώργος στο Γιάννη, ώστε να είναι σίγουρος ότι θα πετύχει την αποστολή του.
τελευταία επεξεργασία από ΘΕΟΔΟΣΙΟΣ ΦΩΤΙΑΔΗΣ σε Παρ Δεκ 28, 2018 2:33 pm, έχει επεξεργασθεί 3 φορές συνολικά.
- ΘΕΟΔΟΣΙΟΣ ΦΩΤΙΑΔΗΣ
- Δημοσιεύσεις: 141
- Εγγραφή: Πέμ Νοέμ 22, 2018 11:47 pm
Re: Διαγωνισμός EMC 2018
Για την 1
Έχουμε: και
και 
Εξισώνοντας τα πρώτα μέλη πέρνουμε:
 .
.
Έχουμε:
 και
και 
Εξισώνοντας τα πρώτα μέλη πέρνουμε:
 .
.
- Άν
 το ζητούμενο έχει αποδειχθεί.
το ζητούμενο έχει αποδειχθεί.
- Άν
 τότε
τότε  , αφού
, αφού  .
.
Από τις συμμετρικές της προκύπτει ότι
προκύπτει ότι  και
και

i)Αν τότε
τότε 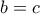 και τελειώσαμε,
και τελειώσαμε,
ii)Aν τότε
τότε  άτοπο αφού
άτοπο αφού  .
.
Άρα ή
ή  , δείξαμε το ζητούμενο.
, δείξαμε το ζητούμενο.
- ΘΕΟΔΟΣΙΟΣ ΦΩΤΙΑΔΗΣ
- Δημοσιεύσεις: 141
- Εγγραφή: Πέμ Νοέμ 22, 2018 11:47 pm
Re: Διαγωνισμός EMC 2018
Παραθέτω και τα θέματα των Seniors προς συζήτηση:
1. Μια διαμέριση ενός θετικού ακεραίου ονομάζεται άρτια, αν όλα της τα στοιχεία είναι άρτιοι αριθμοί, ενώ αντίστοιχα περιττή, αν όλα τα στοιχεία της είναι περιττοί αριθμοί. Να βρεθούν όλοι οι θετικοί ακέραιοι
ονομάζεται άρτια, αν όλα της τα στοιχεία είναι άρτιοι αριθμοί, ενώ αντίστοιχα περιττή, αν όλα τα στοιχεία της είναι περιττοί αριθμοί. Να βρεθούν όλοι οι θετικοί ακέραιοι  ώστε το πλήθος των άρτιων διαμερίσεων να ισούται με το πλήθος των περιττών διαμερίσεων.
ώστε το πλήθος των άρτιων διαμερίσεων να ισούται με το πλήθος των περιττών διαμερίσεων.
Σημείωση: Για τυχαίο θετικό ακέραιο , ονομάζουμε διαμέριση του ακεραίου αυτού οποιαδήποτε μη φθίνουσα ακολουθία
, ονομάζουμε διαμέριση του ακεραίου αυτού οποιαδήποτε μη φθίνουσα ακολουθία  θετικών ακεραίων, για την οποία
θετικών ακεραίων, για την οποία  .
.
2. Θεωρούμε τρίγωνο τον περιγεγραμμένο του κύκλο και το κέντρο αυτού, αντίστοιχα και
τον περιγεγραμμένο του κύκλο και το κέντρο αυτού, αντίστοιχα και  το μέσο του μικρού τόξου
το μέσο του μικρού τόξου  . Έστω
. Έστω 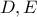 οι δεύτερες τομές του
οι δεύτερες τομές του  με τις από το
με τις από το  κάθετες στις
κάθετες στις  . Τα
. Τα  είναι οι τομές της
είναι οι τομές της  με τις
με τις  . Συμβολίζουμε με
. Συμβολίζουμε με  τους περιγεγραμμένους κύκλους των
τους περιγεγραμμένους κύκλους των  και
και  . Τέλος, ονομάζουμε
. Τέλος, ονομάζουμε  τις τομές των
τις τομές των 
με τις , αντίστοιχα, και
, αντίστοιχα, και  τον περιγεγραμμένο κύκλο του
τον περιγεγραμμένο κύκλο του  .
.
Αν τα κέντρα των
τα κέντρα των  , αντίστοιχα, να αποδειχθεί ότι το
, αντίστοιχα, να αποδειχθεί ότι το  είναι το περίκεντρο του τριγώνου
είναι το περίκεντρο του τριγώνου  .
.
3. Να βρεθούν όλοι οι αριθμοί με την ιδιότητα να υπάρχει φραγμένο σύνολο
με την ιδιότητα να υπάρχει φραγμένο σύνολο  θετικών πραγματικών αριθμών, τέτοιο ώστε για κάθε
θετικών πραγματικών αριθμών, τέτοιο ώστε για κάθε  , να ισχύει ότι
, να ισχύει ότι  .
.
4. Για τους θετικούς ακεραίους εσχύει
εσχύει  , όπου το
, όπου το  εμφανίζεται
εμφανίζεται  φορές και το
φορές και το  ,
,  φορές. Μπορούμε να συμπεράνουμε ότι
φορές. Μπορούμε να συμπεράνουμε ότι  ;
;
1. Μια διαμέριση ενός θετικού ακεραίου
 ονομάζεται άρτια, αν όλα της τα στοιχεία είναι άρτιοι αριθμοί, ενώ αντίστοιχα περιττή, αν όλα τα στοιχεία της είναι περιττοί αριθμοί. Να βρεθούν όλοι οι θετικοί ακέραιοι
ονομάζεται άρτια, αν όλα της τα στοιχεία είναι άρτιοι αριθμοί, ενώ αντίστοιχα περιττή, αν όλα τα στοιχεία της είναι περιττοί αριθμοί. Να βρεθούν όλοι οι θετικοί ακέραιοι  ώστε το πλήθος των άρτιων διαμερίσεων να ισούται με το πλήθος των περιττών διαμερίσεων.
ώστε το πλήθος των άρτιων διαμερίσεων να ισούται με το πλήθος των περιττών διαμερίσεων.Σημείωση: Για τυχαίο θετικό ακέραιο
 , ονομάζουμε διαμέριση του ακεραίου αυτού οποιαδήποτε μη φθίνουσα ακολουθία
, ονομάζουμε διαμέριση του ακεραίου αυτού οποιαδήποτε μη φθίνουσα ακολουθία  θετικών ακεραίων, για την οποία
θετικών ακεραίων, για την οποία  .
.2. Θεωρούμε τρίγωνο
 τον περιγεγραμμένο του κύκλο και το κέντρο αυτού, αντίστοιχα και
τον περιγεγραμμένο του κύκλο και το κέντρο αυτού, αντίστοιχα και  το μέσο του μικρού τόξου
το μέσο του μικρού τόξου  . Έστω
. Έστω 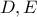 οι δεύτερες τομές του
οι δεύτερες τομές του  με τις από το
με τις από το  κάθετες στις
κάθετες στις  . Τα
. Τα  είναι οι τομές της
είναι οι τομές της  με τις
με τις  . Συμβολίζουμε με
. Συμβολίζουμε με  τους περιγεγραμμένους κύκλους των
τους περιγεγραμμένους κύκλους των  και
και  . Τέλος, ονομάζουμε
. Τέλος, ονομάζουμε  τις τομές των
τις τομές των 
με τις
 , αντίστοιχα, και
, αντίστοιχα, και  τον περιγεγραμμένο κύκλο του
τον περιγεγραμμένο κύκλο του  .
.Αν
 τα κέντρα των
τα κέντρα των  , αντίστοιχα, να αποδειχθεί ότι το
, αντίστοιχα, να αποδειχθεί ότι το  είναι το περίκεντρο του τριγώνου
είναι το περίκεντρο του τριγώνου  .
.3. Να βρεθούν όλοι οι αριθμοί
 με την ιδιότητα να υπάρχει φραγμένο σύνολο
με την ιδιότητα να υπάρχει φραγμένο σύνολο  θετικών πραγματικών αριθμών, τέτοιο ώστε για κάθε
θετικών πραγματικών αριθμών, τέτοιο ώστε για κάθε  , να ισχύει ότι
, να ισχύει ότι  .
.4. Για τους θετικούς ακεραίους
 εσχύει
εσχύει  , όπου το
, όπου το  εμφανίζεται
εμφανίζεται  φορές και το
φορές και το  ,
,  φορές. Μπορούμε να συμπεράνουμε ότι
φορές. Μπορούμε να συμπεράνουμε ότι  ;
;- Διονύσιος Αδαμόπουλος
- Δημοσιεύσεις: 807
- Εγγραφή: Σάβ Μαρ 19, 2016 5:11 pm
- Τοποθεσία: Πύργος Ηλείας
Re: Διαγωνισμός EMC 2018
Καταρχάς εύκολα προκύπτει ότιΘΕΟΔΟΣΙΟΣ ΦΩΤΙΑΔΗΣ έγραψε: ↑Πέμ Δεκ 27, 2018 10:22 pm
2. Θεωρούμε τρίγωνοτον περιγεγραμμένο του κύκλο και το κέντρο αυτού, αντίστοιχα και
το μέσο του μικρού τόξου
. Έστω
οι δεύτερες τομές του
με τις από το
κάθετες στις
. Τα
είναι οι τομές της
με τις
. Συμβολίζουμε με
τους περιγεγραμμένους κύκλους των
και
. Τέλος, ονομάζουμε
τις τομές των
με τις, αντίστοιχα, και
τον περιγεγραμμένο κύκλο του
.
Αντα κέντρα των
, αντίστοιχα, να αποδειχθεί ότι το
είναι το περίκεντρο του τριγώνου
.
 , οπότε
, οπότε  , επομένως
, επομένως  .
.Παρατηρούμε επίσης πως η
 είναι κάθετη στη
είναι κάθετη στη  , άρα εύκολα προκύπτει ότι
, άρα εύκολα προκύπτει ότι  , άρα
, άρα  , συνεπώς το τετράπλευρο
, συνεπώς το τετράπλευρο  είναι εγγράψιμο είναι εγγράψιμο, δηλαδή το
είναι εγγράψιμο είναι εγγράψιμο, δηλαδή το  ανήκει στον
ανήκει στον  και όμοια ανήκει και στον
και όμοια ανήκει και στον  .
.Έστω πως ο
 τέμνει την
τέμνει την  στο
στο  . Έχουμε πως:
. Έχουμε πως: .
. Άρα
 .
.Όμοια αν ο
 τέμνει την
τέμνει την  στο
στο  , τότε
, τότε  .
. Όμως
 , οπότε τελικά
, οπότε τελικά  , δηλαδή οι
, δηλαδή οι  και
και  τέμνονται πάνω στην
τέμνονται πάνω στην  στο
στο  .
.Από το θεώρημα
 λοιπόν συμπεραίνουμε ότι ο
λοιπόν συμπεραίνουμε ότι ο  διέρχεται επίσης από το
διέρχεται επίσης από το  .
.Έχουμε ακόμη ότι
 και
και  , άρα
, άρα 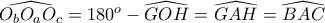 .
.Επιπλέον αφού αφού ο
 είναι ο ριζικός άξονας των
είναι ο ριζικός άξονας των  , έχουμε ότι
, έχουμε ότι  , πιο συγκεκριμένα η
, πιο συγκεκριμένα η  είναι η μεσοκάθετος του
είναι η μεσοκάθετος του  .
.Όμως είναι
 και όμοια είναι
και όμοια είναι  , άρα το
, άρα το 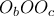 είναι ισοσκελές και
είναι ισοσκελές και  είναι
είναι 
Συνεπώς το
 είναι το περίκεντρο του
είναι το περίκεντρο του  .
.Houston, we have a problem!
Re: Διαγωνισμός EMC 2018
ΘΕΟΔΟΣΙΟΣ ΦΩΤΙΑΔΗΣ έγραψε: ↑Τρί Δεκ 25, 2018 2:38 pmΧαίρετε και καλά Χριστούγεννα
Παραθέτω τα θέματα σε Latex:
1. Αν οι μη μηδενικοί πραγματικοί αριθμοίικανοποιούν τις σχέσεις
να αποδειχθεί οτι δύο απο αυτούς είναι ίσοι.
2. Να βρεθούν όλα τα ζεύγηθετικών ακεραίων, που ικανοποιούν τη σχέση
3. Δίνεται τρίγωνομε
με ορθόκεντρο
. Ο κύκλος με κίντρο
και ακτίνα
τέμνει τον περιγεγραμμένο κύκλο του
στο
, ενώ ο κύκλος κέντρου
και ακτίνας
τέμνει την
στο
. Η από το
παράλληλη στην
τέμνει την
στο
, ενώ
είναι το ίχνος της κάθετης από το
προς την
. Να αποδειχθεί ότι το μέσο την
, το μέσο
της
και το
είναι συνευθειακά.
4. Ο Γιάννης και ο Γιώργος έχουν μπροστά τουςποτήρια στη σειρά. Ο Γιάννης επιλέγει, χωρίς ο Γιώργος να βλέπει, δύο ποτήρια. Κάτω απο το ένα ανοίγει μια τρύπα και κάτω από το άλλο βάζει ένα μπαλάκι. Μία κίνηση αποτελείται απο την εναλλαγή δύο διαδοχικών ποτηριών της σειράς.
Η αποστολή του Γιώργου είναι η εξής: Πρέπει να δώσει μια σειρά από πεπερασμένες κινήσεις στο Γιάννη, τις οποίες ο Γιάννης εκτελεί, οι οποίες θα οδηγήσουν σίγουρα στο να πέσει το μπαλάκι μέσα στην τρύπα. Να βρεθεί ο ελάχιστος αριθμός από κινήσεις τις οποίες πρέπει να δώσει ο Γιώργος στο Γιάννη, ώστε να είναι σίγουρος ότι θα πετύχει την αποστολή του.
 με
με  θετικό ακέραιο. Άρα
θετικό ακέραιο. Άρα 
 περιπτώσεις...
περιπτώσεις...Re: Διαγωνισμός EMC 2018
Για την 1:Αρχικά,ο  πρέπει να είναι ζυγός.Κάθε άρτια διαμέριση
πρέπει να είναι ζυγός.Κάθε άρτια διαμέριση 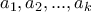 μετατρέπεται σε μια έγκυρη περιττή:Την
μετατρέπεται σε μια έγκυρη περιττή:Την  όπου οι άσσοι στην αρχή είναι
όπου οι άσσοι στην αρχή είναι  .Είναι απλo ότι δυο διαφορετικές άρτιες διαμερίσεις δεν μπορούν να δώσουν την ίδια περιττή(μέσω του παραπάνω μετασχηματισμού),δηλαδή οι περιττές είναι τουλάχιστον όσες οι άρτιες.Για
.Είναι απλo ότι δυο διαφορετικές άρτιες διαμερίσεις δεν μπορούν να δώσουν την ίδια περιττή(μέσω του παραπάνω μετασχηματισμού),δηλαδή οι περιττές είναι τουλάχιστον όσες οι άρτιες.Για  όμως,το
όμως,το  γράφεται με τουλάχιστον 2 τρόπους ως άθροισμα περιττών,άρα οι περιττές διαμερίσεις είναι περισσότερες.Τελικά,
γράφεται με τουλάχιστον 2 τρόπους ως άθροισμα περιττών,άρα οι περιττές διαμερίσεις είναι περισσότερες.Τελικά,  που επαληθεύουν.
που επαληθεύουν.
 πρέπει να είναι ζυγός.Κάθε άρτια διαμέριση
πρέπει να είναι ζυγός.Κάθε άρτια διαμέριση 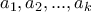 μετατρέπεται σε μια έγκυρη περιττή:Την
μετατρέπεται σε μια έγκυρη περιττή:Την  όπου οι άσσοι στην αρχή είναι
όπου οι άσσοι στην αρχή είναι  .Είναι απλo ότι δυο διαφορετικές άρτιες διαμερίσεις δεν μπορούν να δώσουν την ίδια περιττή(μέσω του παραπάνω μετασχηματισμού),δηλαδή οι περιττές είναι τουλάχιστον όσες οι άρτιες.Για
.Είναι απλo ότι δυο διαφορετικές άρτιες διαμερίσεις δεν μπορούν να δώσουν την ίδια περιττή(μέσω του παραπάνω μετασχηματισμού),δηλαδή οι περιττές είναι τουλάχιστον όσες οι άρτιες.Για  όμως,το
όμως,το  γράφεται με τουλάχιστον 2 τρόπους ως άθροισμα περιττών,άρα οι περιττές διαμερίσεις είναι περισσότερες.Τελικά,
γράφεται με τουλάχιστον 2 τρόπους ως άθροισμα περιττών,άρα οι περιττές διαμερίσεις είναι περισσότερες.Τελικά,  που επαληθεύουν.
που επαληθεύουν.Re: Διαγωνισμός EMC 2018
Με επιφυλάξεις για το 4,ναι μπορούμε.Το  ισοδυναμεί με το
ισοδυναμεί με το  .Έστω
.Έστω  και
και  όπου το
όπου το 
δηλώνει τον αριθμό των εκθετών στον πύργο.
Λογαριθμίζουμε και τα 2 μέλη της αρχικής (βάση ):
): ,δηλαδή
,δηλαδή  και έστω ότι τα
και έστω ότι τα 
είναι πρώτα μεταξύ τους.Θα είναι δηλαδή και επειδή τα
και επειδή τα 
είναι πρώτα μεταξύ τους,υπάρχουν ώστε
ώστε  .Λογαριθμίζοντας την αρχική 2 φορές(βάση
.Λογαριθμίζοντας την αρχική 2 φορές(βάση  ) προκύπτει τελικά ότι
) προκύπτει τελικά ότι  δηλαδή ότι το
δηλαδή ότι το  είναι φυσικός,οπότε υποθέτοντας χωρίς βλάβη της γενικότητας ότι
είναι φυσικός,οπότε υποθέτοντας χωρίς βλάβη της γενικότητας ότι 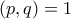 βγαίνει
βγαίνει 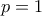 (και επειδή τα
(και επειδή τα  είναι άνισα από υποθεση,δε γίνεται
είναι άνισα από υποθεση,δε γίνεται  ),δηλαδή
),δηλαδή  αλλά και
αλλά και  με
με  φυσικό.Λογαριθμίζοντας 2 φορές την αρχική (βάση
φυσικό.Λογαριθμίζοντας 2 φορές την αρχική (βάση  ),πλέον προκύπτει ότι
),πλέον προκύπτει ότι  το οποίο σημαίνει ότι
το οποίο σημαίνει ότι  ,πράγμα άτοπο κλπ.
,πράγμα άτοπο κλπ.
 ισοδυναμεί με το
ισοδυναμεί με το  .Έστω
.Έστω  και
και  όπου το
όπου το 
δηλώνει τον αριθμό των εκθετών στον πύργο.
Λογαριθμίζουμε και τα 2 μέλη της αρχικής (βάση
 ):
): ,δηλαδή
,δηλαδή  και έστω ότι τα
και έστω ότι τα 
είναι πρώτα μεταξύ τους.Θα είναι δηλαδή
 και επειδή τα
και επειδή τα 
είναι πρώτα μεταξύ τους,υπάρχουν
 ώστε
ώστε  .Λογαριθμίζοντας την αρχική 2 φορές(βάση
.Λογαριθμίζοντας την αρχική 2 φορές(βάση  ) προκύπτει τελικά ότι
) προκύπτει τελικά ότι  δηλαδή ότι το
δηλαδή ότι το  είναι φυσικός,οπότε υποθέτοντας χωρίς βλάβη της γενικότητας ότι
είναι φυσικός,οπότε υποθέτοντας χωρίς βλάβη της γενικότητας ότι 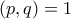 βγαίνει
βγαίνει 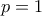 (και επειδή τα
(και επειδή τα  είναι άνισα από υποθεση,δε γίνεται
είναι άνισα από υποθεση,δε γίνεται  ),δηλαδή
),δηλαδή  αλλά και
αλλά και  με
με  φυσικό.Λογαριθμίζοντας 2 φορές την αρχική (βάση
φυσικό.Λογαριθμίζοντας 2 φορές την αρχική (βάση  ),πλέον προκύπτει ότι
),πλέον προκύπτει ότι  το οποίο σημαίνει ότι
το οποίο σημαίνει ότι  ,πράγμα άτοπο κλπ.
,πράγμα άτοπο κλπ.- Demetres
- Γενικός Συντονιστής
- Δημοσιεύσεις: 8989
- Εγγραφή: Δευ Ιαν 19, 2009 5:16 pm
- Τοποθεσία: Λεμεσός/Πύλα
- Επικοινωνία:
Re: Διαγωνισμός EMC 2018
Θα δείξουμε ότι θέλειΘΕΟΔΟΣΙΟΣ ΦΩΤΙΑΔΗΣ έγραψε: ↑Τρί Δεκ 25, 2018 2:38 pm4. Ο Γιάννης και ο Γιώργος έχουν μπροστά τουςποτήρια στη σειρά. Ο Γιάννης επιλέγει, χωρίς ο Γιώργος να βλέπει, δύο ποτήρια. Κάτω απο το ένα ανοίγει μια τρύπα και κάτω από το άλλο βάζει ένα μπαλάκι. Μία κίνηση αποτελείται απο την εναλλαγή δύο διαδοχικών ποτηριών της σειράς.
Η αποστολή του Γιώργου είναι η εξής: Πρέπει να δώσει μια σειρά από πεπερασμένες κινήσεις στο Γιάννη, τις οποίες ο Γιάννης εκτελεί, οι οποίες θα οδηγήσουν σίγουρα στο να πέσει το μπαλάκι μέσα στην τρύπα. Να βρεθεί ο ελάχιστος αριθμός από κινήσεις τις οποίες πρέπει να δώσει ο Γιώργος στο Γιάννη, ώστε να είναι σίγουρος ότι θα πετύχει την αποστολή του.
 κινήσεις.
κινήσεις.Ας δούμε πρώτα πως μπορεί να το πετύχει με τόσες κινήσεις. Αριθμούμε αρχικά τα ποτήρια κατά σειρά από το
 ως το
ως το  . Ακολούθως κάνουμε τις εξής εναλλαγές:
. Ακολούθως κάνουμε τις εξής εναλλαγές:Αλλάζουμε το 1 με το 2, μετά με το 3 κ.ο.κ μέχρι να πάει στην θέση του
 . Δηλαδή τα ποτήρια βρίσκονται τώρα στις θέσεις
. Δηλαδή τα ποτήρια βρίσκονται τώρα στις θέσεις  .
. Μέχρι στιγμής έχουμε κάνει
 κινήσεις. Με άλλες δύο κινήσεις φέρνουμε το
κινήσεις. Με άλλες δύο κινήσεις φέρνουμε το  αριστερά του
αριστερά του  ώστε να έχουμε την διάταξη
ώστε να έχουμε την διάταξη  .
.Συνεχίζοντας με το ίδιο μοτίβο μετά από συνολικά
 κινήσεις φτάνουμε στην διάταξη
κινήσεις φτάνουμε στην διάταξη  . Με άλλες τόσες κινήσεις αναποδογυρίζουμε και την σειρά των άλλων
. Με άλλες τόσες κινήσεις αναποδογυρίζουμε και την σειρά των άλλων  ποτηριών για να φτάσουμε στην διάταξη
ποτηριών για να φτάσουμε στην διάταξη  .
.Τώρα, με άλλες
 κινήσεις παίρνουμε το
κινήσεις παίρνουμε το  τέρμα δεξιά και το
τέρμα δεξιά και το  τέρμα αριστερά για να φτάσουμε στην διάταξη
τέρμα αριστερά για να φτάσουμε στην διάταξη  . Με άλλες
. Με άλλες  κινήσεις παίρνουμε το
κινήσεις παίρνουμε το  τέρμα δεξιά και το
τέρμα δεξιά και το  τέρμα αριστερά. Επαναλαμβάνουμε μέχρι να πάρουμε το
τέρμα αριστερά. Επαναλαμβάνουμε μέχρι να πάρουμε το  τέρμα δεξιά και το
τέρμα δεξιά και το  τέρμα αριστερά. Δηλαδή καταλήγουμε στην διάταξη
τέρμα αριστερά. Δηλαδή καταλήγουμε στην διάταξη  .
. Στην πρώτη φάση κάναμε συνολικά
 κινήσεις ενώ στην δεύτερη κάναμε
κινήσεις ενώ στην δεύτερη κάναμε  κινήσεις από
κινήσεις από  φορές. Συνολικά έχουμε όντως κάνει
φορές. Συνολικά έχουμε όντως κάνει  κινήσεις.
κινήσεις.Παρατηρούμε ότι στην πιο πάνω διαδικασία το κάθε ποτήρι πέρασε από όλες τις θέσεις. Άρα σίγουρα σε κάποια φάση το μπαλάκι θα πέσει μέσα στην τρύπα.
Μένει να δείξουμε ότι σίγουρα χρειάζονται
 κινήσεις. Θα χρησιμοποιήσουμε ένα αρκετά χρήσιμο κόλπο. Θα μπούμε στην θέση ενός πονηρού Γιάννη. Αντί να βάλει την μπάλα κάτω από ένα ποτήρι και να ανοίξει τρύπα κάτω από ένα άλλο στην αρχή θα το κάνει στο τέλος. Απλά πρέπει στο τέλος να μπορεί να πείσει ότι εκεί που ήταν η μπάλα και η τρύπα δεν θα μπορούσε να πέσει η μπάλα στην τρύπα με τις κινήσεις που ζήτησε ο Γιώργος.
κινήσεις. Θα χρησιμοποιήσουμε ένα αρκετά χρήσιμο κόλπο. Θα μπούμε στην θέση ενός πονηρού Γιάννη. Αντί να βάλει την μπάλα κάτω από ένα ποτήρι και να ανοίξει τρύπα κάτω από ένα άλλο στην αρχή θα το κάνει στο τέλος. Απλά πρέπει στο τέλος να μπορεί να πείσει ότι εκεί που ήταν η μπάλα και η τρύπα δεν θα μπορούσε να πέσει η μπάλα στην τρύπα με τις κινήσεις που ζήτησε ο Γιώργος.Αν λοιπόν στις κινήσεις που έδωσε ο Γιώργος υπάρχει ένα ποτήρι που δεν πέρασε πάνω από μια θέση τότε ο Γιάννης μπορεί να ισχυριστεί ότι η μπάλα βρισκόταν σε αυτό το ποτήρι και η τρύπα στην συγκεκριμένη θέση.
Αρκεί λοιπόν να δείξουμε ότι για να περάσει κάθε ποτήρι από κάθε θέση πρέπει να γίνουν τουλάχιστον
 κινήσεις.
κινήσεις.Για να περάσει το ποτήρι
 από όλες τις θέσεις πρέπει στην αρχή να πάει στην μια άκρη, μετά στην άλλη άκρη και μετά να καταλήξει σε μια άλλη θέση
από όλες τις θέσεις πρέπει στην αρχή να πάει στην μια άκρη, μετά στην άλλη άκρη και μετά να καταλήξει σε μια άλλη θέση  .
.Για να πάει το ποτήρι
 στην μια άκρη θέλει τουλάχιστον
στην μια άκρη θέλει τουλάχιστον  κινήσεις αν
κινήσεις αν  και τουλάχιστον
και τουλάχιστον  κινήσεις αν
κινήσεις αν  .
.Συνολικά για να πάνε όλα τα ποτήρια σε μια άκρη χρειάζονται τουλάχιστον
 κινήσεις. Χρειάζονται άλλες
κινήσεις. Χρειάζονται άλλες  κινήσεις για να πάνε στην άλλη άκρη. Τέλος χρειάζονται τουλάχιστον άλλες
κινήσεις για να πάνε στην άλλη άκρη. Τέλος χρειάζονται τουλάχιστον άλλες  κινήσεις για να πάνε τα ποτήρια στις τελικές τους θέσεις. Χρειάζονται τουλάχιστον τόσες από το ίδιο επιχείρημα όπως προηγουμένως αφού οι τελικές θέσεις είναι όλες διαφορετικές.
κινήσεις για να πάνε τα ποτήρια στις τελικές τους θέσεις. Χρειάζονται τουλάχιστον τόσες από το ίδιο επιχείρημα όπως προηγουμένως αφού οι τελικές θέσεις είναι όλες διαφορετικές.Συνολικά λοιπόν χρειάζονται τουλάχιστον
 κινήσεις. Αυτές όμως είναι κινήσεις ποτηριών. Κάθε κίνηση όμως μετακινεί δύο ποτήρια. Άρα συνολικά χρειάζονται τουλάχιστον
κινήσεις. Αυτές όμως είναι κινήσεις ποτηριών. Κάθε κίνηση όμως μετακινεί δύο ποτήρια. Άρα συνολικά χρειάζονται τουλάχιστον  «κανονικές» κινήσεις.
«κανονικές» κινήσεις.-
Xriiiiistos
- Δημοσιεύσεις: 219
- Εγγραφή: Τρί Μάιος 15, 2018 4:36 pm
Re: Διαγωνισμός EMC 2018
ΚΑΛΗ ΧΡΟΝΙΑ ΣΕ ΟΛΟΥΣ !!!
Αρκετά ενδιαφέρον άσκηση (όχι ότι οι άλλες δεν ήταν δεν ήταν)
 μέσα των
μέσα των 
 .
.  το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  . Έίναι γνωστό ότι
. Έίναι γνωστό ότι  ΚΑΙ
ΚΑΙ  διάμετρος του κύκλο του
διάμετρος του κύκλο του  . Αν
. Αν  σημείο της
σημείο της  και
και  τόττε πρέπει
τόττε πρέπει  (αφού
(αφού  λόγο του
λόγο του  ). Όμως παρατηρούμε ότι αν
). Όμως παρατηρούμε ότι αν  τότε ΤΑ ΤΡΙΓΩΝΑ
τότε ΤΑ ΤΡΙΓΩΝΑ  θα είναι ίσα οπότε αρκεί να δείξω
θα είναι ίσα οπότε αρκεί να δείξω  για να λύσω την άσκηση
για να λύσω την άσκηση
 σαν ακτίνες του δεύτερου κύκλου που αναφέρεται στην εκφώνηση. Οπότε τα τρίγωνα
σαν ακτίνες του δεύτερου κύκλου που αναφέρεται στην εκφώνηση. Οπότε τα τρίγωνα  ίσα άρα
ίσα άρα  διχοτομεί την
διχοτομεί την 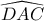 και αφού
και αφού 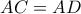 έχουμε
έχουμε  Έστω
Έστω  έχουμε
έχουμε  .
.
 εγγράψιμο.
εγγράψιμο.  η προβολή του
η προβολή του  στην
στην  .
.  αφού
αφού 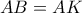 ΣΑΝ ακτίνες του τελαυταίου κύκλου που αναφέρεται και
ΣΑΝ ακτίνες του τελαυταίου κύκλου που αναφέρεται και  αποό το εγγράψιμο
αποό το εγγράψιμο 
Οπότε καταλήγουμε στο εξής .
.

ΘΕΟΔΟΣΙΟΣ ΦΩΤΙΑΔΗΣ έγραψε: ↑Τρί Δεκ 25, 2018 2:38 pm3. Δίνεται τρίγωνομε
με ορθόκεντρο
. Ο κύκλος με κίντρο
και ακτίνα
τέμνει τον περιγεγραμμένο κύκλο του
στο
, ενώ ο κύκλος κέντρου
και ακτίνας
τέμνει την
στο
. Η από το
παράλληλη στην
τέμνει την
στο
, ενώ
είναι το ίχνος της κάθετης από το
προς την
. Να αποδειχθεί ότι το μέσο την
, το μέσο
της
και το
είναι συνευθειακά.
Αρκετά ενδιαφέρον άσκηση (όχι ότι οι άλλες δεν ήταν δεν ήταν)
 μέσα των
μέσα των 
 .
.  το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  . Έίναι γνωστό ότι
. Έίναι γνωστό ότι  ΚΑΙ
ΚΑΙ  διάμετρος του κύκλο του
διάμετρος του κύκλο του  . Αν
. Αν  σημείο της
σημείο της  και
και  τόττε πρέπει
τόττε πρέπει  (αφού
(αφού  λόγο του
λόγο του  ). Όμως παρατηρούμε ότι αν
). Όμως παρατηρούμε ότι αν  τότε ΤΑ ΤΡΙΓΩΝΑ
τότε ΤΑ ΤΡΙΓΩΝΑ  θα είναι ίσα οπότε αρκεί να δείξω
θα είναι ίσα οπότε αρκεί να δείξω  για να λύσω την άσκηση
για να λύσω την άσκηση σαν ακτίνες του δεύτερου κύκλου που αναφέρεται στην εκφώνηση. Οπότε τα τρίγωνα
σαν ακτίνες του δεύτερου κύκλου που αναφέρεται στην εκφώνηση. Οπότε τα τρίγωνα  ίσα άρα
ίσα άρα  διχοτομεί την
διχοτομεί την 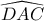 και αφού
και αφού 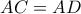 έχουμε
έχουμε  Έστω
Έστω  έχουμε
έχουμε  .
. εγγράψιμο.
εγγράψιμο.  η προβολή του
η προβολή του  στην
στην  .
.  αφού
αφού 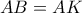 ΣΑΝ ακτίνες του τελαυταίου κύκλου που αναφέρεται και
ΣΑΝ ακτίνες του τελαυταίου κύκλου που αναφέρεται και  αποό το εγγράψιμο
αποό το εγγράψιμο 
Οπότε καταλήγουμε στο εξής
 .
.

-
Τσιαλας Νικολαος
- Δημοσιεύσεις: 789
- Εγγραφή: Σάβ Ιαν 17, 2015 1:04 pm
Re: Διαγωνισμός EMC 2018
Βγήκαν και τα επίσημα αποτελέσματα!! Συγχαρητήρια σε όλα τα παιδιά!! 


http://emc.mnm.hr/competition/results/
http://emc.mnm.hr/competition/results/
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες
