Νομίζω έμεινε αναπάντητο.cretanman έγραψε: ↑Κυρ Απρ 01, 2018 3:52 pmΚαλησπέρα σε όλους!
3ο Θέμα
Δώδεκα φίλοι παίζουν ένα τουρνουά τένις, όπου έκαστος παίζει ένα μόνο παιγνίδι με καθέναν από τους υπόλοιπους έντεκα. Ο νικητής παίρνει ένα βαθμό. Ο ηττημένος παίρνει μηδέν βαθμούς, ενώ δεν υπάρχει ισοπαλία. Οι τελικοί βαθμοί των συμμετεχόντων είναι. Να προσδιορίσετε τη μεγαλύτερη δυνατή τιμή του αθροίσματος
.
Αν δύο άτομα έχουν πάρει τους ίδιους βαθμούς, έστω από
 , τότε αλλάζοντας το μεταξύ τους αποτέλεσμα το
, τότε αλλάζοντας το μεταξύ τους αποτέλεσμα το  αυξάνεται κατά:
αυξάνεται κατά:
Άρα μπορώ να υποθέσω ότι όλοι έχουν πάρει διαφορετικούς βαθμούς. Υπάρχει μόνο ένας τρόπος να συμβεί αυτό και τότε έχουμε


 που είναι τέτοιοι, ώστε
που είναι τέτοιοι, ώστε  .
. .
. .
. , τότε τελειώσαμε, αφού θα είναι
, τότε τελειώσαμε, αφού θα είναι  . Αλλιώς, θα έχουμε
. Αλλιώς, θα έχουμε  .
.

 είναι
είναι  .
. ;
; δεν μπορώ να έχω αυξήσεις επ' άπειρον. Άρα σε κάποια στιγμή όντως θα καταλήξω σε μια κατάσταση όπου όλοι έχουν διαφορετικούς βαθμούς.
δεν μπορώ να έχω αυξήσεις επ' άπειρον. Άρα σε κάποια στιγμή όντως θα καταλήξω σε μια κατάσταση όπου όλοι έχουν διαφορετικούς βαθμούς. , που είναι λύσεις της εξίσωσης:
, που είναι λύσεις της εξίσωσης: 
 είναι περιττός αν εργαστούμε modulo
είναι περιττός αν εργαστούμε modulo  . Παίρνουμε ότι
. Παίρνουμε ότι  που δίνει
που δίνει  . Επειδή όμως ο
. Επειδή όμως ο  είναι περιττός (έχει δειχθεί από τον Αλέξανδρο
είναι περιττός (έχει δειχθεί από τον Αλέξανδρο  Τότε παίρνουμε:
Τότε παίρνουμε: 

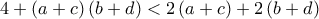 ή
ή  ή
ή 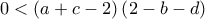 που είναι άτοπο από την υπόθεση.
που είναι άτοπο από την υπόθεση. 

 και
και 

 . Γιατί να ισχύει η ισότητα;
. Γιατί να ισχύει η ισότητα;
 , που θα μας έδινε
, που θα μας έδινε  , και το συμπέρασμα θα ίσχυε "τετριμμένα".
, και το συμπέρασμα θα ίσχυε "τετριμμένα".  , πάρε για παράδειγμα
, πάρε για παράδειγμα  ,
,  ,
, 
 , αλλά
, αλλά 

 σχετικά "κοντά" στο 2, οπότε
σχετικά "κοντά" στο 2, οπότε 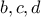 είναι "κοντά" στο 0, τέτοια ώστε
είναι "κοντά" στο 0, τέτοια ώστε  θα είναι "κοντά" στο 0 (όχι στο 1), αφού έχει όρους
θα είναι "κοντά" στο 0 (όχι στο 1), αφού έχει όρους 