Πρόβλημα 3 Δίνεται η αλγεβρική παράσταση

Να απλοποιήσετε την παράσταση
 και να βρείτε το πλήθος των πραγματικών λύσεων της εξίσωσης
και να βρείτε το πλήθος των πραγματικών λύσεων της εξίσωσης  , για κάθε τιμή της παραμέτρου
, για κάθε τιμή της παραμέτρου  .
.Λύση:
Η παράσταση γράφεται ισοδύναμα

 .
.1. Για
![x^2-4 \geq 0 \Leftrightarrow x \in \left (-\infty , -2 \right ] \cup \left [2, +\infty \left ) x^2-4 \geq 0 \Leftrightarrow x \in \left (-\infty , -2 \right ] \cup \left [2, +\infty \left )](/forum/ext/geomar/texintegr/latexrender/pictures/50b2531201a40fd158b675a941551509.png) η εξίσωση γράφεται
η εξίσωση γράφεται
Ο αριθμός των λύσεων της παραπάνω εξίσωσης αντιστοιχεί με τα σημεία τομής της ευθείας
 και της γραφικής παράστασης της συνάρτησης
και της γραφικής παράστασης της συνάρτησης  . Για την
. Για την  είναι
είναι  . Οπότε είναι γνησίως αύξουσα σε καθέ ένα από τα διαστήματα ορισμού της και θα τέμενει σε μοναδικό σημείο την
. Οπότε είναι γνησίως αύξουσα σε καθέ ένα από τα διαστήματα ορισμού της και θα τέμενει σε μοναδικό σημείο την  σε καθένα από αυτά. Σχεδιαζουμε την γραφική παράστασή της
σε καθένα από αυτά. Σχεδιαζουμε την γραφική παράστασή τηςαπλή εποπτεία της οποίας μας δίνει τον αριθμό των λύσεων για τις διάφορες τιμές του
 .
.Δυο λύσεις αν
 .
.Μια λύση αν
 ή
ή 
2. Για
 η εξίσωση γίνεται
η εξίσωση γίνεται 
 ή
ή  .
.Οπότε σε αυτή την περίπτωση έχουμε:
Mια λύση αν

Δυο λύσεις αν

Συνοψίζοντας τις περιπτώσεις (1),(2) έχουμε τελικά
Δυο ρίζες αν

Τρεις ρίζες αν

Τέσσερις ρίζες αν



 είναι το μέσο του τόξου
είναι το μέσο του τόξου  που δεν περιέχει το
που δεν περιέχει το  είναι ρόμβος,ως παραλληλόγραμμο με κάθετες διαγωνίους (ή απλώς επειδή όλες οι πλευρές του είναι ίσες με την ακτίνα).
είναι ρόμβος,ως παραλληλόγραμμο με κάθετες διαγωνίους (ή απλώς επειδή όλες οι πλευρές του είναι ίσες με την ακτίνα). διαιρεί τη διάμεσο
διαιρεί τη διάμεσο  σε λόγο
σε λόγο  είναι το βαρύκεντρο του ισόπλευρου τριγώνου
είναι το βαρύκεντρο του ισόπλευρου τριγώνου  .
. διχοτομεί την γωνία
διχοτομεί την γωνία  κι άρα
κι άρα 
 είναι το αντιδιαμετρικό σημείο της κορυφής
είναι το αντιδιαμετρικό σημείο της κορυφής  , τότε το τετράπλευρο
, τότε το τετράπλευρο  είναι παραλληλόγραμμο.
είναι παραλληλόγραμμο. και
και 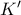 του
του  ως προς τις πλευρές
ως προς τις πλευρές  και
και  είναι συνευθειακά με τα
είναι συνευθειακά με τα  και
και  αντίστοιχα, και θα ανήκουν στον
αντίστοιχα, και θα ανήκουν στον  . Επίσης, ισχύει
. Επίσης, ισχύει  , κι άρα θα ταυτίζονται με τα
, κι άρα θα ταυτίζονται με τα  και
και  , αντίστοιχα.
, αντίστοιχα. και
και  είναι εφαπτόμενα τμήματα του κύκλου
είναι εφαπτόμενα τμήματα του κύκλου  από το
από το  , αφού
, αφού  , κι άρα είναι ίσα.
, κι άρα είναι ίσα. είναι παραληλόγραμμο. Βέβαια, ο ισχυρισμός αυτός έπεται άμεσα αφού
είναι παραληλόγραμμο. Βέβαια, ο ισχυρισμός αυτός έπεται άμεσα αφού  ,
,  και
και  ,
, 
 είναι ισοσκελές τραπέζιο, αφού
είναι ισοσκελές τραπέζιο, αφού 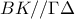 και
και  , κι άρα
, κι άρα 
 . Λόγω της
. Λόγω της  - ρας και Π.Θ. ( επιτρέπεται ; ) ,
- ρας και Π.Θ. ( επιτρέπεται ; ) , και το τρίγωνο προκύπτει ορθογώνιο ...
και το τρίγωνο προκύπτει ορθογώνιο ... η οποία έχει ξεκάθαρα 3 λύσεις.
η οποία έχει ξεκάθαρα 3 λύσεις. στο σχήμα, περιστρέφεται γύρω απ' το σημείο
στο σχήμα, περιστρέφεται γύρω απ' το σημείο  (εξαιρουμένης της κατακόρυφης).
(εξαιρουμένης της κατακόρυφης).  τουλάχιστον σε δύο σημεία (από δύο έως και τέσσερα).
τουλάχιστον σε δύο σημεία (από δύο έως και τέσσερα). και
και  . Εξισώνοντας τα δεξιά μέλη παίρνουμε
. Εξισώνοντας τα δεξιά μέλη παίρνουμε , κι άρα
, κι άρα  .
. .
. και
και 
 οι πράξεις είναι (ίσως) πιο εύκολες.
οι πράξεις είναι (ίσως) πιο εύκολες. και
και  είναι ίση με
είναι ίση με 
 , και
, και και
και 
 , και άρα ο
, και άρα ο 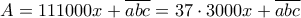
 είναι πολλαπλάσιο του 37.
είναι πολλαπλάσιο του 37. , υπάρχουν
, υπάρχουν  αριθμοί της μορφής
αριθμοί της μορφής  ,
,  , ...,
, ..., 
 , υπάρχουν συνολικά
, υπάρχουν συνολικά  τέτοιοι αριθμοί
τέτοιοι αριθμοί  και
και  και τη διάκριση περιπτώσεων στη συνέχεια.
και τη διάκριση περιπτώσεων στη συνέχεια. και εύκολα βρίσκουμε
και εύκολα βρίσκουμε 

 , κι άρα η εξίσωση γίνεται
, κι άρα η εξίσωση γίνεται  , που δίνει
, που δίνει  (δεκτή).
(δεκτή). .
. , οπότε η εξίσωση γράφεται
, οπότε η εξίσωση γράφεται  , ή ισοδύναμα
, ή ισοδύναμα , που δίνει
, που δίνει  (δεκτή).
(δεκτή). .
.

 από την τριγωνική ανισότητα, δηλαδή, αφού
από την τριγωνική ανισότητα, δηλαδή, αφού  , αν και μόνο αν
, αν και μόνο αν  .
. , τότε
, τότε  , ενώ αν
, ενώ αν  , τότε
, τότε  .
. του πολυγώνου είναι
του πολυγώνου είναι  ,
,  ,
,  ,
,  .
. και
και  , το εμβαδό του είναι
, το εμβαδό του είναι
 , έπεται ότι
, έπεται ότι 