(α) Να παραγοντοποιήσετε το πολυώνυμο
 σε γινόμενο δύο μη σταθερών πολυωνύμων με ακέραιους συντελεστές.
σε γινόμενο δύο μη σταθερών πολυωνύμων με ακέραιους συντελεστές.(β) Να βρείτε όλα τα ζεύγη θετικών ακεραίων
 , για τους οποίους η παράσταση
, για τους οποίους η παράσταση  είναι πρώτος αριθμός.
είναι πρώτος αριθμός.Πρόβλημα 2
Να βρείτε όλες τις τριάδες πραγματικών αριθμών
 , για τις οποίες ισχύουν όλες οι πιο κάτω συνθήκες:
, για τις οποίες ισχύουν όλες οι πιο κάτω συνθήκες:i.

ii.

iii.
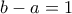
Πρόβλημα 3
Δίνεται οξυγώνιο τρίγωνο
 . Έστω
. Έστω  το μέσον της πλευράς του
το μέσον της πλευράς του  και έστω ότι
και έστω ότι  . Πάνω στην ευθεία
. Πάνω στην ευθεία  παίρνουμε σημείο
παίρνουμε σημείο  , τέτοιο ώστε
, τέτοιο ώστε  . Ονομάζουμε
. Ονομάζουμε  το σημείο τομής της διχοτόμου
το σημείο τομής της διχοτόμου  της γωνίας
της γωνίας  με την ευθεία
με την ευθεία  . Η κάθετη από το σημείο
. Η κάθετη από το σημείο  προς την
προς την  τέμνει την διάμεσο
τέμνει την διάμεσο  στο σημείο
στο σημείο  και την
και την  στο σημείο
στο σημείο  . Θεωρούμε
. Θεωρούμε  τα μέσα των τμημάτων
τα μέσα των τμημάτων  , αντίστοιχα. Αν η παράλληλη από το
, αντίστοιχα. Αν η παράλληλη από το  προς την
προς την  τέμνει την ευθεία
τέμνει την ευθεία  στο σημείο
στο σημείο  , να αποδείξετε ότι
, να αποδείξετε ότι  .
.Πρόβλημα 4
Στον πίνακα είναι γραμμένοι οι εξής αριθμοί:
 άσσοι,
άσσοι,  δυάρια και
δυάρια και  τριάρια. Σε κάθε κίνηση ένας παίκτης μπορεί να σβήσει δύο διαφορετικούς αριθμούς και να γράψει στην θέση τους τον τρίτο αριθμό (Ο παίκτης σβήνει δύο αριθμούς και γράφει μόνο έναν αριθμό.). Το παιγνίδι τελειώνει όταν ο παίκτης δεν μπορεί να κάνει άλλη τέτοια κίνηση.
τριάρια. Σε κάθε κίνηση ένας παίκτης μπορεί να σβήσει δύο διαφορετικούς αριθμούς και να γράψει στην θέση τους τον τρίτο αριθμό (Ο παίκτης σβήνει δύο αριθμούς και γράφει μόνο έναν αριθμό.). Το παιγνίδι τελειώνει όταν ο παίκτης δεν μπορεί να κάνει άλλη τέτοια κίνηση.Κάθε ένας από τους Ανδρέα, Βασίλη και Γιώργο παίζει το παιγνίδι μόνος του ξεχωριστά μέχρι να τελειώσει. Στο τέλος του δικού του παιγνιδιού, ο Ανδρέας θέλει να αφήσει στον πίνακα γραμμένο μόνο έναν άσσο (και κανέναν άλλον αριθμό), ο Βασίλης μόνο ένα δυάρι (και κανέναν άλλον αριθμό) και ο Γιώργος μόνο ένα τριάρι (και κανέναν άλλον αριθμό). Να εξηγήσετε πλήρως ποιοι από τους τρεις μπορούν να πετύχουν τον στόχο τους.



 πρώτος και
πρώτος και  πρέπει
πρέπει 
 θετικοί ακέραιοι πρέπει
θετικοί ακέραιοι πρέπει  άρα
άρα  πρώτος.
πρώτος.
 οπότε για να είναι πρώτος πρέπει
οπότε για να είναι πρώτος πρέπει  και άρα
και άρα  .
.

 και αντικαθιστούμε.
και αντικαθιστούμε.

 παίρνουμε
παίρνουμε  και
και 
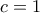 παίρνουμε
παίρνουμε  και
και 
 αφού επείσης το τρίγωνο
αφού επείσης το τρίγωνο 
 γωνίας της θα είναι και ύψος και αφού
γωνίας της θα είναι και ύψος και αφού  ΘΑ ΕΙΝΑΙ
ΘΑ ΕΙΝΑΙ  (
( ). Το
). Το  ορθ.παραλληλόγραμμο άρα
ορθ.παραλληλόγραμμο άρα  άρα
άρα  πλ.παραλληλόγραμμο άρα
πλ.παραλληλόγραμμο άρα 
 πλ.παραλληλόγραμμο οπότε
πλ.παραλληλόγραμμο οπότε  . Έχουμε
. Έχουμε  συνευθειακά από θαλή στο
συνευθειακά από θαλή στο 
 δυάρι και ένα τριάρι. Όμως διαφορά πλήθους δυαριών και τριαριών είναι πάντα περιττός και ποτέ
δυάρι και ένα τριάρι. Όμως διαφορά πλήθους δυαριών και τριαριών είναι πάντα περιττός και ποτέ  .
. τριάρια.Εδώ ακολουθά τα εξής βήματα:
τριάρια.Εδώ ακολουθά τα εξής βήματα:
 ισούται με
ισούται με  .
. που θα βρεις, οπότε μπορεί να μην έχεις τρόπο να
που θα βρεις, οπότε μπορεί να μην έχεις τρόπο να  ή
ή  ή
ή  ,
,  ή
ή  ή
ή  . Οι δύο πρώτες περιπτώσεις τον οδηγούν σε νίκη, οι άλλες δύο όχι, οπότε πρέπει να τις αποφύγει. Πράγμα εύκολο γιατί π.χ. το προηγούμενο βήμα πριν το
. Οι δύο πρώτες περιπτώσεις τον οδηγούν σε νίκη, οι άλλες δύο όχι, οπότε πρέπει να τις αποφύγει. Πράγμα εύκολο γιατί π.χ. το προηγούμενο βήμα πριν το  ή
ή  ή
ή  . Όμως εκεί μπορεί να μεριμνήσει να μην φτάσει γιατί θα παρατηρήσει σε προηγούμενο βήμα ότι αρχίζει και του λείπει κάποιος αριθμός, πράγμα που θα ... τον ξυπνήσει. Τελικά, δεν παίζει τελείως στα κουτουρού αλλά κάθε τόσο προσέχει και, ουσιαστικά, μόνο στα λίγα τελευταία βήματα πονοκεφαλίζει. Όμως μπορεί να διευθετήσει, έστω τελευταία στιγμή, τα άσωτα βήματα μέχρι εκείνη την στιγμή της ζωής του.
. Όμως εκεί μπορεί να μεριμνήσει να μην φτάσει γιατί θα παρατηρήσει σε προηγούμενο βήμα ότι αρχίζει και του λείπει κάποιος αριθμός, πράγμα που θα ... τον ξυπνήσει. Τελικά, δεν παίζει τελείως στα κουτουρού αλλά κάθε τόσο προσέχει και, ουσιαστικά, μόνο στα λίγα τελευταία βήματα πονοκεφαλίζει. Όμως μπορεί να διευθετήσει, έστω τελευταία στιγμή, τα άσωτα βήματα μέχρι εκείνη την στιγμή της ζωής του.

 ,ώστε
,ώστε  ,που είναι πρώτος
,που είναι πρώτος

 τότε από τα (i) και (ii) τα
τότε από τα (i) και (ii) τα  είναι οι ρίζες του πολυωνύμου
είναι οι ρίζες του πολυωνύμου  . Επειδή
. Επειδή  ένα εκ των
ένα εκ των