
Μέγιστη απόσταση σημείων καμπύλης
Συντονιστής: chris_gatos
- chris_gatos
- Επιμελητής
- Δημοσιεύσεις: 6962
- Εγγραφή: Κυρ Δεκ 21, 2008 9:03 pm
- Τοποθεσία: Ανθούπολη
Μέγιστη απόσταση σημείων καμπύλης
Να βρείτε τη μέγιστη απόσταση δύο σημείων της καμπύλης


Χρήστος Κυριαζής
Λέξεις Κλειδιά:
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3341
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Μέγιστη απόσταση σημείων καμπύλης
Ας παρατηρήσουμε κατ' αρχήν ότι η ζητούμενη μέγιστη απόσταση δίδεται από την απόσταση ανάμεσα σε δύο σημεία  ,
,  . Πράγματι, αν η μέγιστη απόσταση δίδεται από την απόσταση ανάμεσα σε δύο μη συμμετρικά ως προς
. Πράγματι, αν η μέγιστη απόσταση δίδεται από την απόσταση ανάμεσα σε δύο μη συμμετρικά ως προς  σημεία
σημεία  ,
,  επί της καμπύλης, τότε ... λαμβάνοντας τα συμμετρικά
επί της καμπύλης, τότε ... λαμβάνοντας τα συμμετρικά  ,
,  ως προς
ως προς  καταλήγουμε σε ένα παραλληλόγραμμο
καταλήγουμε σε ένα παραλληλόγραμμο  όπου είτε
όπου είτε  είτε
είτε  (άτοπο): πράγματι, σε κάθε παραλληλόγραμμο μία τουλάχιστον διαγώνιος (κείμενη απέναντι αμβλείας γωνίας) είναι μεγαλύτερη και των δύο πλευρών.
(άτοπο): πράγματι, σε κάθε παραλληλόγραμμο μία τουλάχιστον διαγώνιος (κείμενη απέναντι αμβλείας γωνίας) είναι μεγαλύτερη και των δύο πλευρών.
Αναζητούμε λοιπόν το μέγιστο της για
για  , δηλαδή για
, δηλαδή για  . Αρκεί επομένως να μεγιστοποιήσουμε την
. Αρκεί επομένως να μεγιστοποιήσουμε την  . Από την
. Από την  συμπεραίνουμε ότι έχουμε μεγιστοποίηση για
συμπεραίνουμε ότι έχουμε μεγιστοποίηση για  . Επιστρέφοντας στην
. Επιστρέφοντας στην  συμπεραίνουμε ότι το ζητούμενο μέγιστο ισούται προς
συμπεραίνουμε ότι το ζητούμενο μέγιστο ισούται προς ![2\sqrt[4]{a^4+b^4} 2\sqrt[4]{a^4+b^4}](/forum/ext/geomar/texintegr/latexrender/pictures/8279f691162f8ef49ddd377c86607799.png) .
.
Τα παραπάνω επαληθεύονται στην περίπτωση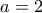 ,
,  , με μέγιστη απόσταση περίπου
, με μέγιστη απόσταση περίπου  :
:
 ,
,  . Πράγματι, αν η μέγιστη απόσταση δίδεται από την απόσταση ανάμεσα σε δύο μη συμμετρικά ως προς
. Πράγματι, αν η μέγιστη απόσταση δίδεται από την απόσταση ανάμεσα σε δύο μη συμμετρικά ως προς  σημεία
σημεία  ,
,  επί της καμπύλης, τότε ... λαμβάνοντας τα συμμετρικά
επί της καμπύλης, τότε ... λαμβάνοντας τα συμμετρικά  ,
,  ως προς
ως προς  καταλήγουμε σε ένα παραλληλόγραμμο
καταλήγουμε σε ένα παραλληλόγραμμο  όπου είτε
όπου είτε  είτε
είτε  (άτοπο): πράγματι, σε κάθε παραλληλόγραμμο μία τουλάχιστον διαγώνιος (κείμενη απέναντι αμβλείας γωνίας) είναι μεγαλύτερη και των δύο πλευρών.
(άτοπο): πράγματι, σε κάθε παραλληλόγραμμο μία τουλάχιστον διαγώνιος (κείμενη απέναντι αμβλείας γωνίας) είναι μεγαλύτερη και των δύο πλευρών.Αναζητούμε λοιπόν το μέγιστο της
 για
για  , δηλαδή για
, δηλαδή για  . Αρκεί επομένως να μεγιστοποιήσουμε την
. Αρκεί επομένως να μεγιστοποιήσουμε την  . Από την
. Από την  συμπεραίνουμε ότι έχουμε μεγιστοποίηση για
συμπεραίνουμε ότι έχουμε μεγιστοποίηση για  . Επιστρέφοντας στην
. Επιστρέφοντας στην  συμπεραίνουμε ότι το ζητούμενο μέγιστο ισούται προς
συμπεραίνουμε ότι το ζητούμενο μέγιστο ισούται προς ![2\sqrt[4]{a^4+b^4} 2\sqrt[4]{a^4+b^4}](/forum/ext/geomar/texintegr/latexrender/pictures/8279f691162f8ef49ddd377c86607799.png) .
.Τα παραπάνω επαληθεύονται στην περίπτωση
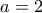 ,
,  , με μέγιστη απόσταση περίπου
, με μέγιστη απόσταση περίπου  :
:Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
- nsmavrogiannis
- Επιμελητής
- Δημοσιεύσεις: 4455
- Εγγραφή: Σάβ Δεκ 20, 2008 7:13 pm
- Τοποθεσία: Αθήνα
- Επικοινωνία:
Re: Μέγιστη απόσταση σημείων καμπύλης
Σε ένα παραλληλόγραμμο κάθε πλευρά είναι μικρότερη από τουλάχιστον μία διαγώνιο. Αυτό μπορεί να επαληθευθεί εύκολα με την τριγωνική ανισότητα ή και τον κανόνα του παραλληλογράμμου: Αν  είναι οι διαγώνιοι και και
είναι οι διαγώνιοι και και  οι πλευρές τότε δεν μπορεί να είναι
οι πλευρές τότε δεν μπορεί να είναι  και
και  διότι τότε θα είχαμε
διότι τότε θα είχαμε 
 δηλαδή
δηλαδή  .
.
Ας ονομάσουμε την καμπύλη η οποία προφανώς έχει άξονα συμμετρίας την αρχή των αξόνων
την καμπύλη η οποία προφανώς έχει άξονα συμμετρίας την αρχή των αξόνων  . Αν
. Αν  είναι δύο σημεία της
είναι δύο σημεία της  και υποτεθεί ότι η ευθεία
και υποτεθεί ότι η ευθεία  δεν διέρχεται από το
δεν διέρχεται από το  τότε ονομάζουμε
τότε ονομάζουμε  τα συμμετρικά τους ως προς
τα συμμετρικά τους ως προς  . Αυτά θα ανήκουν στην καμπύλη και το
. Αυτά θα ανήκουν στην καμπύλη και το  ′ είναι παραλληλόγραμμο. Συνεπώς το μήκος της πλευράς
′ είναι παραλληλόγραμμο. Συνεπώς το μήκος της πλευράς  θα είναι μικρότερο από κάποια διαγώνιο που φυσικά διέρχεται από το
θα είναι μικρότερο από κάποια διαγώνιο που φυσικά διέρχεται από το  .
.
Οι προηγούμενες παρατηρήσεις μας λένε ότι το μέγιστο θα αναζητηθεί σε σημεία που η ευθεία τους διέρχεται από το . Αλλά κάθε τέτοια ευθεία είναι της μορφής
. Αλλά κάθε τέτοια ευθεία είναι της μορφής  και τέμνει την
και τέμνει την  σε δύο σημεία που είναι συμμετρικά ως προς προς
σε δύο σημεία που είναι συμμετρικά ως προς προς  . 'Αρα πρόκειται για σημεία της μορφής
. 'Αρα πρόκειται για σημεία της μορφής  . Η απόσταση τους είναι
. Η απόσταση τους είναι
 . Ζητάμε λοιπόν σημείο
. Ζητάμε λοιπόν σημείο  της
της  ώστε το
ώστε το  να γίνεται μέγιστο.
να γίνεται μέγιστο.
Είναι άρα υπάρχει
άρα υπάρχει  ώστε
ώστε  , \
, \  .
.
Θέλουμε λοιπόν να μεγιστοποιήσουμε το που κατά τα γνωστά γράφεται και
που κατά τα γνωστά γράφεται και  όπου
όπου  και
και  ,
, 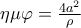 . Η μέγιστη τιμή λοιπόν είναι
. Η μέγιστη τιμή λοιπόν είναι  και επιτυγχάνεται όταν
και επιτυγχάνεται όταν  .
.
edit Έγραφα και δεν είδα το post του Γιώργου. Το αφήνω για τον κόπο μου και για το ότι η λύση στηρίζεται σε γνώσεις Β΄Λυκείου
 είναι οι διαγώνιοι και και
είναι οι διαγώνιοι και και  οι πλευρές τότε δεν μπορεί να είναι
οι πλευρές τότε δεν μπορεί να είναι  και
και  διότι τότε θα είχαμε
διότι τότε θα είχαμε 
 δηλαδή
δηλαδή  .
.Ας ονομάσουμε
 την καμπύλη η οποία προφανώς έχει άξονα συμμετρίας την αρχή των αξόνων
την καμπύλη η οποία προφανώς έχει άξονα συμμετρίας την αρχή των αξόνων  . Αν
. Αν  είναι δύο σημεία της
είναι δύο σημεία της  και υποτεθεί ότι η ευθεία
και υποτεθεί ότι η ευθεία  δεν διέρχεται από το
δεν διέρχεται από το  τότε ονομάζουμε
τότε ονομάζουμε  τα συμμετρικά τους ως προς
τα συμμετρικά τους ως προς  . Αυτά θα ανήκουν στην καμπύλη και το
. Αυτά θα ανήκουν στην καμπύλη και το  ′ είναι παραλληλόγραμμο. Συνεπώς το μήκος της πλευράς
′ είναι παραλληλόγραμμο. Συνεπώς το μήκος της πλευράς  θα είναι μικρότερο από κάποια διαγώνιο που φυσικά διέρχεται από το
θα είναι μικρότερο από κάποια διαγώνιο που φυσικά διέρχεται από το  .
.Οι προηγούμενες παρατηρήσεις μας λένε ότι το μέγιστο θα αναζητηθεί σε σημεία που η ευθεία τους διέρχεται από το
 . Αλλά κάθε τέτοια ευθεία είναι της μορφής
. Αλλά κάθε τέτοια ευθεία είναι της μορφής  και τέμνει την
και τέμνει την  σε δύο σημεία που είναι συμμετρικά ως προς προς
σε δύο σημεία που είναι συμμετρικά ως προς προς  . 'Αρα πρόκειται για σημεία της μορφής
. 'Αρα πρόκειται για σημεία της μορφής  . Η απόσταση τους είναι
. Η απόσταση τους είναι  . Ζητάμε λοιπόν σημείο
. Ζητάμε λοιπόν σημείο  της
της  ώστε το
ώστε το  να γίνεται μέγιστο.
να γίνεται μέγιστο. Είναι
 άρα υπάρχει
άρα υπάρχει  ώστε
ώστε  , \
, \  .
. Θέλουμε λοιπόν να μεγιστοποιήσουμε το
 που κατά τα γνωστά γράφεται και
που κατά τα γνωστά γράφεται και  όπου
όπου  και
και  ,
, 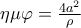 . Η μέγιστη τιμή λοιπόν είναι
. Η μέγιστη τιμή λοιπόν είναι  και επιτυγχάνεται όταν
και επιτυγχάνεται όταν  .
.edit Έγραφα και δεν είδα το post του Γιώργου. Το αφήνω για τον κόπο μου και για το ότι η λύση στηρίζεται σε γνώσεις Β΄Λυκείου
Αν κανείς δεν ελπίζει, δεν θα βρεί το ανέλπιστο, οι δρόμοι για το ανεξερεύνητο θα είναι κλειστοί.
Ηράκλειτος
Ηράκλειτος
- matha
- Γενικός Συντονιστής
- Δημοσιεύσεις: 6423
- Εγγραφή: Παρ Μάιος 21, 2010 7:40 pm
- Τοποθεσία: Θεσσαλονίκη
Re: Μέγιστη απόσταση σημείων καμπύλης
Το πιάνω από κει που το άφησε ο Νίκος: Θέλουμε να μεγιστοποιήσουμε την παράσταση  υπό το δεσμό
υπό το δεσμό 
Από την ανισότητα Cauchy-Schwarz είναι
![\displaystyle{1=\frac{x^4}{a^4}+\frac{y^4}{b^4}\geq \frac{(x^2+y^2)^2}{a^4+b^4}\implies d\leq 2\sqrt[4]{a^4+b^4}.} \displaystyle{1=\frac{x^4}{a^4}+\frac{y^4}{b^4}\geq \frac{(x^2+y^2)^2}{a^4+b^4}\implies d\leq 2\sqrt[4]{a^4+b^4}.}](/forum/ext/geomar/texintegr/latexrender/pictures/12ab76748e444cad1e8fa90e85837e56.png)
Η ισότητα πιάνεται όταν![\displaystyle{|x|=\frac{a^2}{\sqrt[4]{a^4+b^4}},|y|=\frac{b^2}{\sqrt[4]{a^4+b^4}}} \displaystyle{|x|=\frac{a^2}{\sqrt[4]{a^4+b^4}},|y|=\frac{b^2}{\sqrt[4]{a^4+b^4}}}](/forum/ext/geomar/texintegr/latexrender/pictures/51a72228a3ccbd9e1d9c6256f2072c52.png) .
.
Άρα![\displaystyle{d_{\max}=2\sqrt[4]{a^4+b^4}.} \displaystyle{d_{\max}=2\sqrt[4]{a^4+b^4}.}](/forum/ext/geomar/texintegr/latexrender/pictures/a75f0f37ba68742eabaf444ec31264e5.png)
 υπό το δεσμό
υπό το δεσμό 
Από την ανισότητα Cauchy-Schwarz είναι
![\displaystyle{1=\frac{x^4}{a^4}+\frac{y^4}{b^4}\geq \frac{(x^2+y^2)^2}{a^4+b^4}\implies d\leq 2\sqrt[4]{a^4+b^4}.} \displaystyle{1=\frac{x^4}{a^4}+\frac{y^4}{b^4}\geq \frac{(x^2+y^2)^2}{a^4+b^4}\implies d\leq 2\sqrt[4]{a^4+b^4}.}](/forum/ext/geomar/texintegr/latexrender/pictures/12ab76748e444cad1e8fa90e85837e56.png)
Η ισότητα πιάνεται όταν
![\displaystyle{|x|=\frac{a^2}{\sqrt[4]{a^4+b^4}},|y|=\frac{b^2}{\sqrt[4]{a^4+b^4}}} \displaystyle{|x|=\frac{a^2}{\sqrt[4]{a^4+b^4}},|y|=\frac{b^2}{\sqrt[4]{a^4+b^4}}}](/forum/ext/geomar/texintegr/latexrender/pictures/51a72228a3ccbd9e1d9c6256f2072c52.png) .
.Άρα
![\displaystyle{d_{\max}=2\sqrt[4]{a^4+b^4}.} \displaystyle{d_{\max}=2\sqrt[4]{a^4+b^4}.}](/forum/ext/geomar/texintegr/latexrender/pictures/a75f0f37ba68742eabaf444ec31264e5.png)
Μάγκος Θάνος
Re: Μέγιστη απόσταση σημείων καμπύλης
Χρήστο καλημέρα...και μια άλλη ιδέα...chris_gatos έγραψε: ↑Σάβ Ιαν 12, 2019 12:08 amΝα βρείτε τη μέγιστη απόσταση δύο σημείων της καμπύλης

Εργαζόμαστε στο ακόλουθο σχήμα:
Από τη μορφή της εξίσωσης (1) εύκολα διαπιστώνει κανείς ότι η
καμπύλη
 έχει ως άξονες συμμετρίας τους άξονες
έχει ως άξονες συμμετρίας τους άξονες 
καθώς και ένα κέντρο συμμετρίας την αρχή των αξόνων
 .
.Με δεδομένα αυτά μπορεί να υποστηρίξουμε ότι τα σημεία εκείνα
που έχουν τη μέγιστη απόσταση θα είναι πάνω σε μια "διάμετρο".
"Διάμετρο" θα λέμε εκείνη τη χορδή της καμπύλης
 αυτής που διέρχεται
αυτής που διέρχεται από το κέντρο αυτής. Αυτό δείχνεται ως εξής:
Έστω
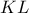 , μια τυχαία χορδή της καμπύλης
, μια τυχαία χορδή της καμπύλης  .
. Τότε από την τριγωνική ανισότητα θα είναι:

Όμως τα τμήματα
 είναι μισά της αντίστοιχης "διαμέτρου" που
είναι μισά της αντίστοιχης "διαμέτρου" που αυτά ορίζουν και συνεπώς θα είναι μικρότερα από εκείνη τη "διάμετρο"

η οποία θα είναι η μέγιστη.
Άρα η από την (2) προκύπτει:

Ύστερα από αυτά μένει να βρούμε ποια είναι η μέγιστη διάμετρος της
 .
.Αναζήτηση της μέγιστης "διαμέτρου"
Εργαζόμαστε στο δεύτερο σχήμα:
Από την εξίσωση (1) έχουμε:

Έτσι θα είναι:

Αν μελετήσουμε την
 ουσιαστικά μελετάμε τη μεταβολή του μεγέθους
ουσιαστικά μελετάμε τη μεταβολή του μεγέθους και όλης της διαμέτρου

Είναι διαδοχικά :




Από την τελευταία μορφή εύκολα μελετάται το πρόσημο της παραγώγου και κατά συνέπεια τα ακρότατα της
 .
. Έτσι το μέγιστο παρατηρείται για την τιμή:
![\displaystyle{x=\frac{a^2}{\sqrt[4]{a^4+b^4} }\ \ (6)} \displaystyle{x=\frac{a^2}{\sqrt[4]{a^4+b^4} }\ \ (6)}](/forum/ext/geomar/texintegr/latexrender/pictures/9f274516722907ab09531740967d61a6.png)
και το ελάχιστο για την τιμή

Η μέγιστη αυτή θέση της διαμέτρου εμφανίζεται στο τρίτο σχήμα:
Κώστας Δόρτσιος
ΥΓ1. Τα τρία σχήματα σχεδιάστηκαν με τιμές
 μονάδες μήκους.
μονάδες μήκους.ΥΓ2. Αφού βρέθηκε η τετμηνένη της θέσης του μεγίστου εύκολα προσδιορίζεται και η τιμή του μεγίστου.
ΥΓ3. Θα μπορούσαμε να κάνουμε και ολόκληρη τη μεταβολή της διαμέτρου.
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Μέγιστη απόσταση σημείων καμπύλης
Δεν χρειάζεται παραλληλόγραμμο.gbaloglou έγραψε: ↑Σάβ Ιαν 12, 2019 8:23 pmΑς παρατηρήσουμε κατ' αρχήν ότι η ζητούμενη μέγιστη απόσταση δίδεται από την απόσταση ανάμεσα σε δύο σημεία,
. Πράγματι, αν η μέγιστη απόσταση δίδεται από την απόσταση ανάμεσα σε δύο μη συμμετρικά ως προς
σημεία
,
επί της καμπύλης, τότε ... λαμβάνοντας τα συμμετρικά
,
ως προς
καταλήγουμε σε ένα παραλληλόγραμμο
όπου είτε
είτε
(άτοπο): πράγματι, σε κάθε παραλληλόγραμμο μία τουλάχιστον διαγώνιος (κείμενη απέναντι αμβλείας γωνίας) είναι μεγαλύτερη και των δύο πλευρών.
Αν θέσουμε
 τότε από τριγωνική έχουμε
τότε από τριγωνική έχουμε 
Αλλά θα είναι

Προφανώς
 και
και 
όπου
 τα συμμετρικά των
τα συμμετρικά των  αντίστοιχα.
αντίστοιχα.Αρα η μέγιστη απόσταση λαμβάνεται για συμμετρικά σημεία
- Γιώργος Ρίζος
- Επιμελητής
- Δημοσιεύσεις: 5284
- Εγγραφή: Δευ Δεκ 29, 2008 1:18 pm
- Τοποθεσία: Κέρκυρα
Re: Μέγιστη απόσταση σημείων καμπύλης
Καλησπέρα σε όλους. Mια προσπάθεια με τη μέθοδο του τριωνύμου.
Έστω ο κύκλος με εξίσωση
Αναζητούμε την αναγκαία και ικανή συνθήκη ώστε να τέμνει την καμπύλη.
Είναι οπότε η εξίσωση της καμπύλης γίνεται
οπότε η εξίσωση της καμπύλης γίνεται

Για να έχουμε σημεία τομής πρέπει να είναι


 .
.
H ελάχιστη τιμή του , για να έχει κοινά σημεία με την καμπύλη είναι
, για να έχει κοινά σημεία με την καμπύλη είναι  .
.
Η μέγιστη ακτίνα του κύκλου δίνει δύο διπλές ρίζες για το που είναι οι τετμημένες των σημείων επαφής κύκλου και καμπύλης.
που είναι οι τετμημένες των σημείων επαφής κύκλου και καμπύλης.
Κάθε σημείο της καμπύλης, εκτός των σημείων επαφής είναι εσωτερικό του κύκλου, άρα μέγιστη απόσταση έχουμε για δύο αντιδιαμετρικά σημεία επαφής.
Έστω αυτά τα σημεία.
αυτά τα σημεία.
Οπότε , με τη μέγιστη μεταξύ τους απόσταση
, με τη μέγιστη μεταξύ τους απόσταση ![\displaystyle 2R = 2\sqrt[4]{{{a^4} + {b^4}}} \displaystyle 2R = 2\sqrt[4]{{{a^4} + {b^4}}}](/forum/ext/geomar/texintegr/latexrender/pictures/4ffdce6cbbd359ef5c68be77f81edf95.png) .
.
edit Έκανα μια αλλαγή στη διατύπωση σε σχέση με την αρχική ανάρτηση και μια προσθήκη για το ελάχιστο της ακτίνας .
.
Έστω ο κύκλος με εξίσωση

Αναζητούμε την αναγκαία και ικανή συνθήκη ώστε να τέμνει την καμπύλη.
Είναι
 οπότε η εξίσωση της καμπύλης γίνεται
οπότε η εξίσωση της καμπύλης γίνεται
Για να έχουμε σημεία τομής πρέπει να είναι


 .
.H ελάχιστη τιμή του
 , για να έχει κοινά σημεία με την καμπύλη είναι
, για να έχει κοινά σημεία με την καμπύλη είναι  .
.Η μέγιστη ακτίνα του κύκλου δίνει δύο διπλές ρίζες για το
 που είναι οι τετμημένες των σημείων επαφής κύκλου και καμπύλης.
που είναι οι τετμημένες των σημείων επαφής κύκλου και καμπύλης.Κάθε σημείο της καμπύλης, εκτός των σημείων επαφής είναι εσωτερικό του κύκλου, άρα μέγιστη απόσταση έχουμε για δύο αντιδιαμετρικά σημεία επαφής.
Έστω
 αυτά τα σημεία.
αυτά τα σημεία.Οπότε
 , με τη μέγιστη μεταξύ τους απόσταση
, με τη μέγιστη μεταξύ τους απόσταση ![\displaystyle 2R = 2\sqrt[4]{{{a^4} + {b^4}}} \displaystyle 2R = 2\sqrt[4]{{{a^4} + {b^4}}}](/forum/ext/geomar/texintegr/latexrender/pictures/4ffdce6cbbd359ef5c68be77f81edf95.png) .
.edit Έκανα μια αλλαγή στη διατύπωση σε σχέση με την αρχική ανάρτηση και μια προσθήκη για το ελάχιστο της ακτίνας
 .
.
τελευταία επεξεργασία από Γιώργος Ρίζος σε Δευ Ιαν 14, 2019 1:20 pm, έχει επεξεργασθεί 1 φορά συνολικά.
- gbaloglou
- Επιμελητής
- Δημοσιεύσεις: 3341
- Εγγραφή: Παρ Φεβ 27, 2009 10:24 pm
- Τοποθεσία: Θεσσαλονικη
- Επικοινωνία:
Re: Μέγιστη απόσταση σημείων καμπύλης
Γιώργο πολύ ωραία η προσπάθεια, ίσως να μην επαρκεί ως έχει για αυστηρή απόδειξη, μας δίνει όμως έναν πανέμορφο χαρακτηρισμό της μέγιστης απόστασης, κάτι που είχα αναζητήσει και εγώ (ανεπιτυχώς, κυρίως επειδή δεν πίστεψα ότι υπάρχει)!
Γιώργος Μπαλόγλου -- κρυσταλλογράφω άρα υπάρχω
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Ὁρᾷς, τὸ κάλλος ὅσσον ἐστὶ τῆς λίθου, ἐν ταῖς ἀτάκτοις τῶν φλεβῶν εὐταξίαις. -- Παλατινή Ανθολογία 9.695 -- Ιδού του πετραδιού η άμετρη ομορφιά, μεσ' των φλεβών τις άναρχες πειθαρχίες.
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
