 με βαρύκεντρο
με βαρύκεντρο 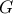 και έγκεντρο
και έγκεντρο  Οι
Οι  τέμνουν τον περιγεγραμμένο κύκλο στα σημεία
τέμνουν τον περιγεγραμμένο κύκλο στα σημεία  αντίστοιχα.
αντίστοιχα.Αν το τρίγωνο είναι ισοσκελές, είναι τετριμμένο ότι ισχύει
 Είναι όμως δυνατόν να ισχύει
Είναι όμως δυνατόν να ισχύει  και σε μη ισοσκελή τρίγωνα. Αποδείξτε όμως τότε ότι ισχύει
και σε μη ισοσκελή τρίγωνα. Αποδείξτε όμως τότε ότι ισχύει 
Συντονιστής: gbaloglou
 με βαρύκεντρο
με βαρύκεντρο 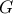 και έγκεντρο
και έγκεντρο  Οι
Οι  τέμνουν τον περιγεγραμμένο κύκλο στα σημεία
τέμνουν τον περιγεγραμμένο κύκλο στα σημεία  αντίστοιχα.
αντίστοιχα. Είναι όμως δυνατόν να ισχύει
Είναι όμως δυνατόν να ισχύει  και σε μη ισοσκελή τρίγωνα. Αποδείξτε όμως τότε ότι ισχύει
και σε μη ισοσκελή τρίγωνα. Αποδείξτε όμως τότε ότι ισχύει 
Καλημέρα Θάνο! Είναι
 και
και 
 παίρνω:
παίρνω: 
 άρα καταλήγω σε
άρα καταλήγω σε 
 ώστε
ώστε  για κάθε
για κάθε  και βρίσκω
και βρίσκω 
 που δίνει περίπου
που δίνει περίπου 
 και βγήκε
και βγήκε 
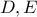 από το αρχικό σχήμα της εκφώνησης.
από το αρχικό σχήμα της εκφώνησης.Και εγώ καταλήγω στην ίδια σχέση Γιώργο, από την οποία προκύπτει
 οπότε
οπότε 
Όμορφο θέμα.
 Θα δούμε το θέμα υπό το πρίσμα της κατασκευής του, αφού όπως θα δούμε είναι κατασκευάσιμο, αν έχουμε σαν βάση την χορδή
Θα δούμε το θέμα υπό το πρίσμα της κατασκευής του, αφού όπως θα δούμε είναι κατασκευάσιμο, αν έχουμε σαν βάση την χορδή 
 το κέντρο του κύκλου και
το κέντρο του κύκλου και  το αντιδιαμετρικό του
το αντιδιαμετρικό του 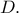 Αν
Αν  είναι η τομή της εφαπτομένης του κύκλου στο
είναι η τομή της εφαπτομένης του κύκλου στο  με την ημιευθεία
με την ημιευθεία  και
και  , τότε, τα
, τότε, τα  είναι αρμονικά συζυγή των
είναι αρμονικά συζυγή των  αφού η ημιευθεία
αφού η ημιευθεία  είναι διχοτόμος της
είναι διχοτόμος της 
 είναι τομή του κύκλου
είναι τομή του κύκλου  με τον Απολλώνιο κύκλο διαμέτρου
με τον Απολλώνιο κύκλο διαμέτρου  αφετέρου έχουμε:
αφετέρου έχουμε: 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες