Τέλεια ... σχέση

Tolaso J Kos · #1

Αν η διαίρεση $\left( x^3 + \alpha x + \beta \right): \left( x - \rho \right)^2$ είναι τέλεια , τότε να δειχθεί ότι για τους πραγματικούς αριθμούς $\alpha, \beta$ ισχύει η σχέση:

$\displaystyle{\left ( \frac{\alpha}{3} \right )^3 + \left ( \frac{\beta}{2} \right )^2 =0 }$

#2

Η διαίρεση αυτή δίνει πηλίκο x+2r

και υπόλοιπο (a+3r^2)x+(b-2r^3).

Αν η διαίρεση είναι τέλεια τότε a=-3r^2

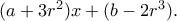
και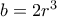

οπότε $\displaystyle{\left ( \frac{\alpha}{3} \right )^3 + \left ( \frac{\beta}{2} \right )^2 =-r^6+r^6=0 }$

#3

Tolaso J Kos έγραψε: ↑
Παρ Δεκ 21, 2018 10:49 am
Αν η διαίρεση $\left( x^3 + \alpha x + \beta \right): \left( x - \rho \right)^2$ είναι τέλεια , τότε να δειχθεί ότι για τους πραγματικούς αριθμούς $\alpha, \beta$ ισχύει η σχέση:

$\displaystyle{\left ( \frac{\alpha}{3} \right )^3 + \left ( \frac{\beta}{2} \right )^2 =0 }$

Λίγο διαφορετικά.

$\displaystyle {x^3} + ax + b = {(x - r)^2}(x - k) = {x^3} - (k + 2r){x^2} + (2kr + {r^2})x - {r^2}k = 0 \Leftrightarrow$

$\displaystyle \left\{ \begin{array}{l} k + 2r = 0\\ \\ 2kr + {r^2} = a\\ \\ - {r^2}k = b \end{array} \right. \Rightarrow a = - 3{r^2} \wedge b = 2{r^3} \Rightarrow {\left( {\frac{a}{3}} \right)^2} + {\left( {\frac{b}{2}} \right)^2} = 0$

#4

Tolaso J Kos έγραψε: ↑
Παρ Δεκ 21, 2018 10:49 am
Αν η διαίρεση $\left( x^3 + \alpha x + \beta \right): \left( x - \rho \right)^2$ είναι τέλεια , τότε να δειχθεί ότι για τους πραγματικούς αριθμούς $\alpha, \beta$ ισχύει η σχέση:

$\displaystyle{\left ( \frac{\alpha}{3} \right )^3 + \left ( \frac{\beta}{2} \right )^2 =0 }$

Και μία εκτός φακέλου: Η υπόθεση είναι ότι το $\rho$ είναι διπλή ρίζα. Συνεπώς είναι ρίζα της παραγώγου, που σημαίνει ότι ισχύει $3\rho ^2+ a =0$ , ισοδύναμα $\rho ^2 = -\frac {a}{3}$ . Άρα

$\displaystyle{\beta ^2 = (-\rho ^3-a\rho )^2= \rho ^2(-\rho ^2 - a) ^2= \left ( -\frac {a}{3} \right ) \left ( \frac {a}{3}- a \right )^2= -\frac {a}{3} \left (- \frac {2a}{3}\right )^2}$ ,

και λοιπά.

Υπάρχουν και άλλοι τρόποι, π.χ. με Vieta.

#5

Μη ξεχνάμε και την διακρίνουσα ...

#6

rek2 έγραψε: ↑
Παρ Δεκ 21, 2018 8:51 pm
Μη ξεχνάμε και την διακρίνουσα ...

Ακριβώς.

Γι' αυτούς που ίσως δεν κατανόησαν τι εννοεί ο Κώστας, επισημαίνω: Αυτό που λέει η αρχική άσκηση είναι "η τριτοβάθμια έχει διπλή ρίζα αν και μόνον αν η διακρίνουσά της είναι

".

Η παράσταση στην άσκηση είναι ισοδύναμη με την πρόταση αυτή. Υπενθυμίζω, η διακρίνουσα είναι η -4a^3 -27b^2

. Βλέπε π.χ. εδώ.

Τέλεια ... σχέση

Τέλεια ... σχέση

Re: Τέλεια ... σχέση

Re: Τέλεια ... σχέση

Re: Τέλεια ... σχέση

Re: Τέλεια ... σχέση

Re: Τέλεια ... σχέση

Μέλη σε σύνδεση