 εφάπτεται ευθείας στο σημείο
εφάπτεται ευθείας στο σημείο  .Πάνω στην ευθεία και εκατέρωθεν του
.Πάνω στην ευθεία και εκατέρωθεν του  έστω τα σημεία
έστω τα σημεία  .
.Φέρνω το ( άλλο ) εφαπτόμενο τμήμα
 στον κύκλο
στον κύκλο  και τον περιγεγραμμένο κύκλο
και τον περιγεγραμμένο κύκλο  του τριγώνου
του τριγώνου  που τέμνει, ακόμα , τον
που τέμνει, ακόμα , τον  στο σημείο
στο σημείο  .
.Αν
 η προβολή του
η προβολή του  στην
στην  , δείξετε ότι :
, δείξετε ότι :  .
.
 . Τότε
. Τότε 




 εφάπτεται της
εφάπτεται της  στο
στο  και συνεπώς το
και συνεπώς το  είναι το (ένα) κοινό εφαπτόμενο τμήμα των κύκλων
είναι το (ένα) κοινό εφαπτόμενο τμήμα των κύκλων  , άρα η κοινή τους χορδή
, άρα η κοινή τους χορδή  (ριζικός άξονας) διέρχεται από το μέσο του
(ριζικός άξονας) διέρχεται από το μέσο του  .
.

 ομοκυκλικά, άρα
ομοκυκλικά, άρα  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.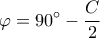
 Άρα η
Άρα η 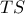 είναι διχοτόμος της
είναι διχοτόμος της 


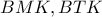 είναι όμοια, άρα
είναι όμοια, άρα  και λόγω του ορθογωνίου
και λόγω του ορθογωνίου  θα είναι και
θα είναι και  και το ζητούμενο έπεται.
και το ζητούμενο έπεται.