τριγωνικομετρικό και λογαριθμικό

Chatzibill · #1

Να υπολογιστεί το ολοκλήρωμα $\huge \int_{\frac{\pi }{6}}^{\frac{\pi }{3}}ln(tanx)dx$
Προσωπικά με δυσκόλεψε αρκετά και μου πήρε 2 μέρες να το λύσω, μου άρεσε αρκετά η λύση μου. Θα την ανεβάσω αύριο εάν δεν υπάρξει παρόμοια.

Tolaso J Kos · #2

Chatzibill έγραψε: ↑
Τρί Δεκ 18, 2018 11:25 pm
Να υπολογιστεί το ολοκλήρωμα $\huge \int_{\frac{\pi }{6}}^{\frac{\pi }{3}}ln(tanx)dx$

Είναι διαδοχικά:

$\displaystyle{\begin{aligned} \int_{\pi/6}^{\pi/3} \log \tan x \, \mathrm{d}x &\overset{u=\tan x}{=\! =\! =\! =\! =\!}\underbrace{\int_{\sqrt{3}/3}^{\sqrt{3}} \frac{\log u}{1+u^2} \, \mathrm{d}u }_{\mathcal{J}}\\ &\overset{u\leftrightarrow 1/u}{=\! =\! =\! =\!} \int_{\sqrt{3}}^{\sqrt{3}/3} \frac{\log \frac{1}{u}}{1+\left ( \frac{1}{u} \right )^2} \cdot \left ( -\frac{1}{u^2} \right ) \, \mathrm{d}u \\ &=-\underbrace{\int_{\sqrt{3}/3}^{\sqrt{3}} \frac{\log u}{1+u^2} \, \mathrm{d}u}_{\mathcal{J}} \end{aligned}}$
Άρα $\mathcal{J} = - \mathcal{J} \Leftrightarrow \mathcal{J} = 0$ .

Tolaso J Kos · #3

Και με Fourier ...

Είναι γνωστό ότι $\displaystyle{\log \tan x = \sum_{n \;\; \text{odd}} \frac{\cos 2n x}{n}}$ . Τότε:

$\displaystyle{\begin{aligned} \int_{\pi/6}^{\pi/3}\log \tan x \, \mathrm{d}x &= \int_{\pi/6}^{\pi/3} \sum_{n \;\; \text{odd}} \frac{\cos 2n x}{n} \, \mathrm{d}x\\ &=\sum_{n \;\; \text{odd}} \frac{1}{n} \int_{\pi/6}^{\pi/3} \cos 2n x \, \mathrm{d}x \\ &=\sum_{n\;\; \text{odd}} \frac{1}{n} \left ( \frac{\sin \frac{2\pi n}{3}- \sin \frac{\pi n}{3}}{2n} \right ) \\ &= \frac{1}{2} \sum_{n=1}^{\infty} \frac{\sin \frac{2\pi \left ( 2n+1 \right )}{3} - \sin \frac{\pi (2n+1)}{3}}{(2n+1)^2}\\ &= \frac{1}{2} {\color{red}{\cancelto{0}{\sum_{n=1}^{\infty} \frac{\cancelto{0}{\sin 4 \pi n}}{\left ( 2n+1 \right )^2}}}} + \frac{1}{2} {\color{red}{\cancelto{0}{\sum_{n=1}^{\infty} \frac{\cancelto{0}{\sin 2 \pi n} }{\left ( 2n+1 \right )^2}}}} \\ &= 0 \end{aligned}}$
διότι $\sin 4 \pi n =0$ διά κάθε $n \in \mathbb{N}$ και $\sin 2 \pi n =0$ διά κάθε $n \in \mathbb{N}$ .

#4

Chatzibill έγραψε: ↑
Τρί Δεκ 18, 2018 11:25 pm
Να υπολογιστεί το ολοκλήρωμα $\huge \int_{\frac{\pi }{6}}^{\frac{\pi }{3}}ln(tanx)dx$

Πιο απλά, η αλλαγή μεταβλητής $\displaystyle{y = \frac {\pi}{2}-x}$ δίνει

$J = - \huge \int_{\frac{\pi }{3}}^{\frac{\pi }{6}}\ln (\tan ( \frac {\pi}{2}-y))dy = \huge \int_{\frac{\pi }{6}}^{\frac{\pi }{3}}\ln (\cot y)dy =-\huge \int_{\frac{\pi }{6}}^{\frac{\pi }{3}}\ln (\tan y)dy=-J$

Άρα J=0

.

Chatzibill · #5

$\huge f(x)=ln(\tan x) Ισχύει ότι , x\in (0,\frac{\pi }{2})$ , $\huge f(x)=ln(tanx)=-ln(\frac{1}{tanx})=-ln(\frac{cosx}{sinx})=-ln(\frac{sin(\frac{\pi }{2}-x)}{cos(\frac{\pi}{2}-x)})=-ln(tan(\frac{\pi }{2}-x))=-f(\frac{\pi }{2}-x)$ .
Άρα $\huge \jmath =\int_{\frac{\pi }{6}}^{\frac{\pi }{3}}f(x)dx=\int_{\frac{\pi }{6}}^{\frac{\pi }{3}}-f(\frac{\pi }{2}-x)dx \overset{\frac{\pi }{2}-x=t, dx=-dt}{\rightarrow} \int_{\frac{\pi }{3}}^{\frac{\pi }{6}}-f(t)(-dt)=-\int_{\frac{\pi }{6}}^{\frac{\pi }{3}}f(t)dt=-\imath \Leftrightarrow 2\imath =0\Leftrightarrow \imath =0$

Η γραφική παράσταση της συνάρτησης $\huge f$

. Μπορούμε να ισχυριστούμε ότι η συνάρτηση f έχει κάποιο είδος συμμετρίας ως προς το $\huge \frac{\pi }{4}$ και για αυτό το ολοκλήρωμα ισούται με 0 ;

Tolaso J Kos · #6

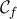Έστω $f(x) = \ln \tan x \;\; , \;\; x \in \left[ \frac{\pi}{6}, \frac{\pi}{3} \right]$ . Για κάθε $x \in \left[ \frac{\pi}{6}, \frac{\pi}{3} \right]$ είναι $\frac{\pi}{2}-x \in \left[ \frac{\pi}{6}, \frac{\pi}{3} \right]$ . Θα δείξουμε ότι η $\mathcal{C}_f$ είναι συμμετρική γύρω απ' το σημείο $\mathrm{A} \left( \frac{\pi}{4} , 0 \right)$ .

$\displaystyle{\begin{aligned} f(x) + f \left ( 2 \cdot \frac{\pi}{4} -x \right ) &= f(x) + f \left ( \frac{\pi}{2} -x \right ) \\ &=\ln \tan x + \ln \cot x \\ &=\ln \tan x- \ln \tan x \\ &=0 \\ &= 2 \cdot 0 \end{aligned}}$
και η απόδειξη ολοκληρώθηκε.

τριγωνικομετρικό και λογαριθμικό

τριγωνικομετρικό και λογαριθμικό

Re: τριγωνικομετρικό και λογαριθμικό

Re: τριγωνικομετρικό και λογαριθμικό

Re: τριγωνικομετρικό και λογαριθμικό

Re: τριγωνικομετρικό και λογαριθμικό

Re: τριγωνικομετρικό και λογαριθμικό

Μέλη σε σύνδεση