 συνεχής και τέτοια ώστε
συνεχής και τέτοια ώστε  για κάθε
για κάθε  . Να υπολογιστεί το όριο:
. Να υπολογιστεί το όριο: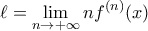
Συντονιστές: grigkost, Κοτρώνης Αναστάσιος
 συνεχής και τέτοια ώστε
συνεχής και τέτοια ώστε  για κάθε
για κάθε  . Να υπολογιστεί το όριο:
. Να υπολογιστεί το όριο: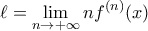

ΓιαTolaso J Kos έγραψε: ↑Κυρ Δεκ 16, 2018 7:16 pmΈστωσυνεχής και τέτοια ώστε
για κάθε
. Να υπολογιστεί το όριο:
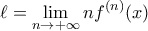
 έχουμε
έχουμε  . Εύκολα βλέπουμε επαγωγικά ότι
. Εύκολα βλέπουμε επαγωγικά ότι  οπότε
οπότε 
 είναι
είναι  . Με άλλα λόγια
. Με άλλα λόγια 
 το αριστερό μέλος τείνει στο
το αριστερό μέλος τείνει στο  οπότε έχουμε, για κάθε
οπότε έχουμε, για κάθε 

 έχουμε τελικά
έχουμε τελικά  , δηλαδή ισότητα παντού. Και λοιπά.
, δηλαδή ισότητα παντού. Και λοιπά. δεν το έκανα αλλά δεν βλέπω ουσιαστικό πρόβλημα).
δεν το έκανα αλλά δεν βλέπω ουσιαστικό πρόβλημα).Από την παραπάνω βλέπουμε ότι
 (1)
(1) (2)
(2)

τότε δεν χρειάζεται να κάνουμε τα παρακάτω. Μπορούμε ήδη να ολοκληρώσουμε
 άρα
άρα 
Όχι Μιχάλη δεν την πάτησα.Mihalis_Lambrou έγραψε: ↑Δευ Δεκ 17, 2018 5:40 pmΣταύρο, σωστά αλλά αν είναι να χρησιμοποιήσουμε την εναλλαγή ορίου και αθροίσματος
που χρησιμοποιείς εδώ
τότε δεν χρειάζεται να κάνουμε τα παρακάτω. Μπορούμε ήδη να ολοκληρώσουμε
την απόδειξη από το προηγούμενο βήμα λέγοντας
άρα
και τελειώσαμε.
Ο λόγος που έκανα τα επόμενα βήματα ήταν ακριβώς για να μην επικαλεσθώ αλλά να αποδείξω την εναλλαγή.

Σταύρο, ίσως σε ερμηνεύω λάθος αλλά η απόδειξή μου δεν λέει αυτό. Λέει,
 τον τύπο της
τον τύπο της  , παίρνω όριο
, παίρνω όριο  . Δεν μπαίνει ανισότητα στον συλλογισμό.
. Δεν μπαίνει ανισότητα στον συλλογισμό.Μιχάλη δεν καταλαβαίνω.Mihalis_Lambrou έγραψε: ↑Δευ Δεκ 17, 2018 7:20 pmΣταύρο, ίσως σε ερμηνεύω λάθος αλλά η απόδειξή μου δεν λέει αυτό. Λέει,
αφού πολλαπλασιάσω επίτον τύπο της
, παίρνω όριο
. Δεν μπαίνει ανισότητα στον συλλογισμό.


 (1)
(1) (2)
(2)

 . Είναι τότε (με εναλλαγή ορίου και άθροισης)
. Είναι τότε (με εναλλαγή ορίου και άθροισης)  .
. Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες