 τριγώνου
τριγώνου  φέρνουμε εφαπτόμενες στον περίκυκλό του, που τέμνουν τις
φέρνουμε εφαπτόμενες στον περίκυκλό του, που τέμνουν τις  στα
στα 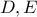
αντίστοιχα. Αν
 είναι ένα κοινό σημείο των κύκλων
είναι ένα κοινό σημείο των κύκλων 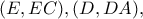 να υπολογίσετε τη γωνία
να υπολογίσετε τη γωνία 
Συντονιστές: vittasko, silouan, Doloros
 τριγώνου
τριγώνου  φέρνουμε εφαπτόμενες στον περίκυκλό του, που τέμνουν τις
φέρνουμε εφαπτόμενες στον περίκυκλό του, που τέμνουν τις  στα
στα 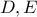
 είναι ένα κοινό σημείο των κύκλων
είναι ένα κοινό σημείο των κύκλων 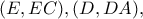 να υπολογίσετε τη γωνία
να υπολογίσετε τη γωνία 
Για να μην μείνει αναπάντητη η πρόταση (πιθανότατα υπάρχει και γωνιακή λύση αλλά προς στιγμή μου διαφεύγει μια "παραλληλία") ας δούμε μια μετρική μπελαλίδικη λύση (αναλυτικά οι πράξεις) .george visvikis έγραψε: ↑Πέμ Νοέμ 08, 2018 12:33 pmΓωνία απ' το πουθενά.png
Από τις κορυφέςτριγώνου
φέρνουμε εφαπτόμενες στον περίκυκλό του, που τέμνουν τις
στα
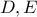
αντίστοιχα. Ανείναι ένα κοινό σημείο των κύκλων
να υπολογίσετε τη γωνία

 είναι
είναι  . Από την προφανή ομοιότητα (γωνιακό κριτήριο) των τριγώνων
. Από την προφανή ομοιότητα (γωνιακό κριτήριο) των τριγώνων  προκύπτει ότι:
προκύπτει ότι: 


 θα έχουμε:
θα έχουμε:




![\Rightarrow {a^2}{c^2} \cdot \left[ {\dfrac{{{a^2}}}{{{{\left( {{a^2} - {b^2}} \right)}^2}}} + \dfrac{{{c^2}}}{{{{\left( {{c^2} - {b^2}} \right)}^2}}} - \dfrac{{{a^2} + {c^2} - {b^2}}}{{\left( {{a^2} - {b^2}} \right)\left( {{c^2} - {b^2}} \right)}}} \right] = \Rightarrow {a^2}{c^2} \cdot \left[ {\dfrac{{{a^2}}}{{{{\left( {{a^2} - {b^2}} \right)}^2}}} + \dfrac{{{c^2}}}{{{{\left( {{c^2} - {b^2}} \right)}^2}}} - \dfrac{{{a^2} + {c^2} - {b^2}}}{{\left( {{a^2} - {b^2}} \right)\left( {{c^2} - {b^2}} \right)}}} \right] =](/forum/ext/geomar/texintegr/latexrender/pictures/f395a8f668cfa30f79ea040ae1e72391.png)
![{a^2}{c^2} \cdot \left[ {\dfrac{{{b^2}}}{{{{\left( {{a^2} - {b^2}} \right)}^2}}} + \dfrac{{{b^2}}}{{{{\left( {{c^2} - {b^2}} \right)}^2}}} - 2\dfrac{{{b^2}}}{{\left( {{a^2} - {b^2}} \right)\left( {{c^2} - {b^2}} \right)}}\cos \theta } \right] {a^2}{c^2} \cdot \left[ {\dfrac{{{b^2}}}{{{{\left( {{a^2} - {b^2}} \right)}^2}}} + \dfrac{{{b^2}}}{{{{\left( {{c^2} - {b^2}} \right)}^2}}} - 2\dfrac{{{b^2}}}{{\left( {{a^2} - {b^2}} \right)\left( {{c^2} - {b^2}} \right)}}\cos \theta } \right]](/forum/ext/geomar/texintegr/latexrender/pictures/5eabb50d6c94a46c2183a4b7687eaa83.png)



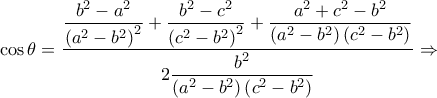


 και το ζητούμενο έχει υπολογιστεί
και το ζητούμενο έχει υπολογιστεί ,μια αντιστροφή με οποιονδήποτε από αυτούς θα κρατούσε σταθερό τον περίκυκλο.Αν πχ. αντιστρέψουμε με κύκλο τον
,μια αντιστροφή με οποιονδήποτε από αυτούς θα κρατούσε σταθερό τον περίκυκλο.Αν πχ. αντιστρέψουμε με κύκλο τον  του σχήματος,ο
του σχήματος,ο θα πάει στον εαυτό του.Επειδή επιπλέον κόβονται αρμονικά οι
θα πάει στον εαυτό του.Επειδή επιπλέον κόβονται αρμονικά οι  (επί της
(επί της  ),το αντίστροφο του
),το αντίστροφο του  θα είναι το
θα είναι το  .(ουσιαστικά άμεσο από την ορθογωνιότητα).Τώρα,οι
.(ουσιαστικά άμεσο από την ορθογωνιότητα).Τώρα,οι  θα είναι αντίστροφοι,επειδή ο αντίστροφος του
θα είναι αντίστροφοι,επειδή ο αντίστροφος του  περνάει από τα
περνάει από τα  (και είναι κάθετος στον
(και είναι κάθετος στον  -η αντιστροφή διατηρεί τις γωνίες μεταξύ των καμπύλων).Άρα είναι ο
-η αντιστροφή διατηρεί τις γωνίες μεταξύ των καμπύλων).Άρα είναι ο  .Επειδή η αντιστροφή διατηρεί τις γωνίες,οι γωνίες μεταξύ των
.Επειδή η αντιστροφή διατηρεί τις γωνίες,οι γωνίες μεταξύ των 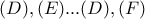 θα είναι ίσες μεταξύ τους.Το ίδιο ισχύει για όλα τα ανά δύο ζεύγη κύκλων,οπότε "παίζοντας" λίγο καταλήγουμε ότι οι κύκλοι τέμνονται σε γωνίες
θα είναι ίσες μεταξύ τους.Το ίδιο ισχύει για όλα τα ανά δύο ζεύγη κύκλων,οπότε "παίζοντας" λίγο καταλήγουμε ότι οι κύκλοι τέμνονται σε γωνίες  μοιρών (ή
μοιρών (ή  ,εξαρτάται πως θα το δει κανείς).
,εξαρτάται πως θα το δει κανείς). (1)
(1) αν και μόνο αν από νόμο συνημιτόνων στο
αν και μόνο αν από νόμο συνημιτόνων στο  ισχύει
ισχύει  (2)
(2) )
)
 (3)
(3)


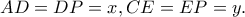 Θα δείξω ότι
Θα δείξω ότι 


 παίρνουμε
παίρνουμε  .
. 
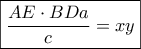





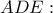


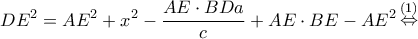
 οπότε
οπότε 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 0 επισκέπτες