perpendicular έγραψε: ↑Τετ Νοέμ 07, 2018 5:14 am
Έστω

συνεχής.Δείξτε ότι τα επόμενα είναι ισοδύναμα:
(i)
![f(\sqrt{xy})\leq \frac{1}{2}\left[f(x)+f(y)\right ],\forall x\forall y\in \left ( 0,+\infty \right ) f(\sqrt{xy})\leq \frac{1}{2}\left[f(x)+f(y)\right ],\forall x\forall y\in \left ( 0,+\infty \right )](/forum/ext/geomar/texintegr/latexrender/pictures/b1fae50b852094be39acc5db1c41ccd7.png)
(ii)η συνάρτηση

ώστε

είναι κυρτή
Η άσκηση περιέχεται στο βιβλίο
Fundamentals of Convex Analysis των Jeans-Baptiste Hiriart-Urruty & Claude Lemarechal στο οποίο δεν περιέχεται η λύση της και την βρήκα ενδιαφέρουσα αρκετά.Η συνεπαγωγή

είναι αρκετά εύκολη.
Καλημέρα Γιώργο. Και η

εύκολη είναι αν γνωρίζουμε ότι για να εξετάσουμε αν μια συνεχής
συνάρτηση είναι κυρτή αρκεί να ισχύει ο ορισμός για

ή οποιοδήποτε άλλο

. Η απόδειξη δεν είναι απλή αλλά περνάει μέσα από τους ρητούς και την ολοκληρώνει η
συνέχεια. Δες midpoint convexity. Με αυτό σαν δεδομένο έχουμε:
Έστω
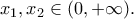
Υπάρχουν

ώστε

και

.
Από την υπόθεση τώρα παίρνουμε την

και η απόδειξη έχει ολοκληρωθεί ως προς την πρώτη συνεπαγωγή. Την άλλη την αφήνω ως εύκολη όπως είπες.
 συνεχής.Δείξτε ότι τα επόμενα είναι ισοδύναμα:
συνεχής.Δείξτε ότι τα επόμενα είναι ισοδύναμα:![f(\sqrt{xy})\leq \frac{1}{2}\left[f(x)+f(y)\right ],\forall x\forall y\in \left ( 0,+\infty \right ) f(\sqrt{xy})\leq \frac{1}{2}\left[f(x)+f(y)\right ],\forall x\forall y\in \left ( 0,+\infty \right )](/forum/ext/geomar/texintegr/latexrender/pictures/b1fae50b852094be39acc5db1c41ccd7.png)
 ώστε
ώστε  είναι κυρτή
είναι κυρτή είναι αρκετά εύκολη.
είναι αρκετά εύκολη.
 εύκολη είναι αν γνωρίζουμε ότι για να εξετάσουμε αν μια συνεχής
εύκολη είναι αν γνωρίζουμε ότι για να εξετάσουμε αν μια συνεχής  ή οποιοδήποτε άλλο
ή οποιοδήποτε άλλο  . Η απόδειξη δεν είναι απλή αλλά περνάει μέσα από τους ρητούς και την ολοκληρώνει η
. Η απόδειξη δεν είναι απλή αλλά περνάει μέσα από τους ρητούς και την ολοκληρώνει η 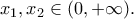 Υπάρχουν
Υπάρχουν  ώστε
ώστε  και
και  .
. 
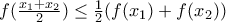







![\lim_{m\rightarrow \infty }\frac{\left [ 2^{m} \lambda \right ]}{2^{m}}=\lambda \lim_{m\rightarrow \infty }\frac{\left [ 2^{m} \lambda \right ]}{2^{m}}=\lambda](/forum/ext/geomar/texintegr/latexrender/pictures/314903da0d0dec9d499ec380ab373ead.png)
![f(\frac{\left [ 2^{m} \lambda \right ]}{2^{m}}x+(1-\frac{\left [ 2^{m} \lambda \right ]}{2^{m}})y)\leq \frac{\left [ 2^{m} \lambda \right ]}{2^{m}}f(x)+(1-\frac{\left [ 2^{m} \lambda \right ]}{2^{m}})f(y) f(\frac{\left [ 2^{m} \lambda \right ]}{2^{m}}x+(1-\frac{\left [ 2^{m} \lambda \right ]}{2^{m}})y)\leq \frac{\left [ 2^{m} \lambda \right ]}{2^{m}}f(x)+(1-\frac{\left [ 2^{m} \lambda \right ]}{2^{m}})f(y)](/forum/ext/geomar/texintegr/latexrender/pictures/5c4e13fc1af487d3de56ed05fa73f6ae.png)


 μου πήρε ώρα να περάσω στο τυχαίο
μου πήρε ώρα να περάσω στο τυχαίο .
.