exdx έγραψε: ↑Τετ Οκτ 31, 2018 1:23 pm
Α. Δίνεται η συνάρτηση με τύπο

α) Να αποδείξετε ότι είναι παραγωγίσιμη στο

.
β) Να αποδείξετε ότι είναι κυρτή στο

.
Β. Δίνεται η δύο φορές παραγωγίσιμη στο

συνάρτηση

και έστω ότι η ευθεία

με εξίσωση

εφάπτεται της

στο σημείο

.
α) Να αποδείξετε ότι η συνάρτηση με τύπο

είναι παραγωγίσιμη στο

.
β) Αν επιπλέον η

είναι τρεις φορές παραγωγίσιμη και κυρτή στο

με

, τότε η

είναι κυρτή στο

.
Υ.Γ. : Ενδεχομένως το τελευταίο ερώτημα να μπορεί να απαντηθεί μόνο με την απαίτηση η

να είναι δύο φορές παραγωγίσιμη
και κυρτή στο

.
Καλό βράδυ κ.Καλαθάκη. Στο Β, και όσον αφορά την

, νομίζω ότι πρέπει να μπουν κάποιοι περιορισμοί για την

π.χ. κυρτή .
Γράφω μια λύση για το Βα) με τη προυπόθεση ότι

κυρτή. Ισχύει το γενικό αποτέλεσμα

από το οποίο παίρνουμε αμέσως

Το παραπάνω προκύπτει από μια εφαρμογή του DLH. Έτσι λοιπόν έχουμε

και


.
Άρα

παραγωγίσιμη στο

και κατά τα γνωστά παραγωγίσιμη και σε όλα τα υπόλοιπα σημεία.
Edit: Μια εφαρμογή του DLH όχι δύο. Ευχαριστώ τον κ.Καλαθάκη για την παρατήρηση.

 .
. .
. συνάρτηση
συνάρτηση  και έστω ότι η ευθεία
και έστω ότι η ευθεία  με εξίσωση
με εξίσωση 
 στο σημείο
στο σημείο  .
.  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  .
. είναι τρεις φορές παραγωγίσιμη στο
είναι τρεις φορές παραγωγίσιμη στο  με
με  , τότε η
, τότε η  είναι κυρτή στο
είναι κυρτή στο  .
.
 , νομίζω ότι πρέπει να μπουν κάποιοι περιορισμοί για την
, νομίζω ότι πρέπει να μπουν κάποιοι περιορισμοί για την  π.χ. κυρτή .
π.χ. κυρτή .



 .
. και κατά τα γνωστά παραγωγίσιμη και σε όλα τα υπόλοιπα σημεία.
και κατά τα γνωστά παραγωγίσιμη και σε όλα τα υπόλοιπα σημεία. με
με  ή
ή επομένως
επομένως  και στο
και στο  έχουμε
έχουμε  και επειδή
και επειδή  άρα
άρα  και
και  και επειδή
και επειδή  άρα
άρα  επομένως παραγωγίσιμη και στο
επομένως παραγωγίσιμη και στο 
 παραγωγίζοντας έχουμε ότι
παραγωγίζοντας έχουμε ότι 

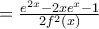 και τελικά
και τελικά 
 είναι
είναι  και
και  άρα η
άρα η  επομένως για
επομένως για  και για
και για  έτσι η
έτσι η 
 αφού και
αφού και  είναι
είναι  και για
και για  αφού και
αφού και  είναι
είναι  η
η 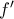
 και
και  τότε η
τότε η  δεν ισχύει.
δεν ισχύει.