
Να δειχθεί ότι για

ισχύει

Συμπλήρωμα.
Ευχαριστώ τον Λάμπρο Κατσάπα για την επισήμανση του τυπογραφικού.Διορθώθηκε
Συντονιστής: KAKABASBASILEIOS



Στη δεξιά μάλλον κάτι έχει ξεφύγει κ.Σταύρο. Ξανακοιτάξτε την. Κάνω την αριστερή.

 για
για  Άρα αρκεί να
Άρα αρκεί να  ή ισοδύναμα
ή ισοδύναμα ή ισοδύναμα
ή ισοδύναμα  που ισχύει γιατί
που ισχύει γιατί  είναι
είναι ![\cos x \in (0,1] \Rightarrow \cos x \ln (\cos x)\leq 0 \cos x \in (0,1] \Rightarrow \cos x \ln (\cos x)\leq 0](/forum/ext/geomar/texintegr/latexrender/pictures/cbb14281b87632063fbe82fbd04ef205.png) (''='' μόνο όταν
(''='' μόνο όταν  )
) 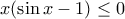 προφανώς (''='' μόνο όταν
προφανώς (''='' μόνο όταν  ).
).
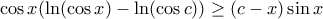 και διαιρώντας με
και διαιρώντας με 
 . Διακρίνουμε τώρα τις περιπτώσεις:
. Διακρίνουμε τώρα τις περιπτώσεις: 
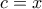 ισχύει η ισότητα.
ισχύει η ισότητα. διαιρούμε με
διαιρούμε με  και παίρνουμε την ισοδύναμη
και παίρνουμε την ισοδύναμη 

![[x,c] [x,c]](/forum/ext/geomar/texintegr/latexrender/pictures/7f2d12542ce69152f4ad7d5378f06fc2.png) υπάρχει
υπάρχει  στο ανοικτό ώστε
στο ανοικτό ώστε 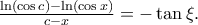
 ισοδύναμα γράφεται
ισοδύναμα γράφεται  που ισχύει αφού
που ισχύει αφού  .
. διαιρούμε με
διαιρούμε με  και παίρνουμε την ισοδύναμη
και παίρνουμε την ισοδύναμη 

![[c,x] [c,x]](/forum/ext/geomar/texintegr/latexrender/pictures/b6a11d661c7a939d9342576e4406cb40.png) υπάρχει
υπάρχει  στο ανοικτό ώστε
στο ανοικτό ώστε 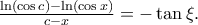
 ισοδύναμα γράφεται
ισοδύναμα γράφεται  που ισχύει αφού
που ισχύει αφού  .
. ισχύει
ισχύει 
 οπότε αρκεί να δειχθεί ότι
οπότε αρκεί να δειχθεί ότι  ισχύει
ισχύει 


 προκύπτει άμεσα η αριστερή.
προκύπτει άμεσα η αριστερή. παίρνει μέγιστη τιμή στο
παίρνει μέγιστη τιμή στο 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες