 είναι το κέντρο του ημικυκλίου . Εξηγήστε γιατί είναι :
είναι το κέντρο του ημικυκλίου . Εξηγήστε γιατί είναι :  .
.Υπολογίστε τα μήκη αυτών των ίσων τμημάτων συναρτήσει της ακτίνας
 .
.Συντονιστές: silouan, Doloros, george visvikis
 είναι το κέντρο του ημικυκλίου . Εξηγήστε γιατί είναι :
είναι το κέντρο του ημικυκλίου . Εξηγήστε γιατί είναι :  .
. .
.Το βλέπω ανάδρομα .
 , ακτίνας
, ακτίνας  και
και  σημείο
σημείο  , τότε το
, τότε το  Φέρνω κάθετη το κέντρο
Φέρνω κάθετη το κέντρο  στο
στο  . Προφανώς
. Προφανώς  και αφού η πλευρά
και αφού η πλευρά  δηλαδή το
δηλαδή το  έχει πλευρές:
έχει πλευρές:  Αν τώρα
Αν τώρα  , σημείο της ακτίνας
, σημείο της ακτίνας  με
με  φέρνω τη
φέρνω τη 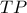 που τέμνει την
που τέμνει την  στο
στο  .
. από το Θ. Μενελάου με διατέμνουσα
από το Θ. Μενελάου με διατέμνουσα 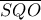 έχω :
έχω :  και άρα :
και άρα :  αλλά και
αλλά και  συνεπώς
συνεπώς 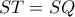
Έστω
 η προβολή του
η προβολή του  στη διάμετρο και
στη διάμετρο και 


 άρα η
άρα η 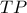 διχοτομεί τη
διχοτομεί τη  και κατά συνέπεια
και κατά συνέπεια 
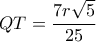 κι επειδή
κι επειδή  με νόμο συνημιτόνων βρίσκουμε
με νόμο συνημιτόνων βρίσκουμε 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες