 , με
, με  , ο κύκλος
, ο κύκλος  τέμνει την
τέμνει την  στο
στο  και
καιτον περίκυκλο του τριγώνου στο
 . Δείξτε ότι η ευθεία
. Δείξτε ότι η ευθεία 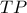 και η διχοτόμος της
και η διχοτόμος της 
τέμνονται πάνω στον περίκυκλο του τριγώνου .
Συντονιστές: silouan, Doloros, george visvikis
 , με
, με  , ο κύκλος
, ο κύκλος  τέμνει την
τέμνει την  στο
στο  και
και . Δείξτε ότι η ευθεία
. Δείξτε ότι η ευθεία 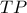 και η διχοτόμος της
και η διχοτόμος της 
 του τριγώνου
του τριγώνου  ως γνωστό διέρχεται από το νότιο πόλο , έστω
ως γνωστό διέρχεται από το νότιο πόλο , έστω  , του κύκλου
, του κύκλου 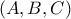 .
.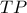 είναι φορέας της διχοτόμου του τριγώνου
είναι φορέας της διχοτόμου του τριγώνου  .
. το κέντρο του κύκλου
το κέντρο του κύκλου 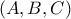 και
και  το σημείο τομής της
το σημείο τομής της  με τον κύκλο
με τον κύκλο  .
. είναι ισογώνια γιατί η εγγεγραμμένη γωνία είναι το μισό της αντίστοιχης επικέντρου .
είναι ισογώνια γιατί η εγγεγραμμένη γωνία είναι το μισό της αντίστοιχης επικέντρου .  είναι ισοσκελές με κορυφή το
είναι ισοσκελές με κορυφή το  και η διχοτόμος της
και η διχοτόμος της  με άμεση συνέπεια
με άμεση συνέπεια  .
. και άρα η
και άρα η 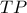 θα διέρχεται από το νότιο πόλο
θα διέρχεται από το νότιο πόλο  .
. το κοινό σημείο τομής της
το κοινό σημείο τομής της  με τον κύκλο
με τον κύκλο  .
. του κύκλου
του κύκλου 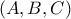 είναι ίσες άρα:
είναι ίσες άρα: 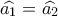 .
.  είναι
είναι  και η
και η  κοινή.
κοινή.  ( άτοπο) , άρα είναι ίσα και έτσι
( άτοπο) , άρα είναι ίσα και έτσι  του κύκλου
του κύκλου  να είναι ίσα .
να είναι ίσα . είναι έγκεντρο του
είναι έγκεντρο του  με άμεση συνέπεια οι διχοτόμοι των
με άμεση συνέπεια οι διχοτόμοι των  να συντρέχουν στο νότιο πόλο του κύκλου
να συντρέχουν στο νότιο πόλο του κύκλου 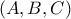 .
.Η
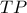 τέμενει τον περίκυκλο του τριγώνου
τέμενει τον περίκυκλο του τριγώνου  στο σημείο
στο σημείο 
 είναι η διχοτόμος του τριγώνου
είναι η διχοτόμος του τριγώνου 


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες