Ναι φαίνεται ,στα μάτια τα δικά μου,προβληματικό.
Συμβολικά μπορούμε να γράψουμε

και τα δύο έχουν νόημα επειδή η συνάρτηση είναι συνεχής.
Όμως χωρίς να υπολογίσουμε (έμμεσα ή με οποιονδήποτε τρόπο να μας είναι γνωστή) την αρχική (παράγουσα) της συνάρτηση θα καταφύγουμε ας πούμε(με την σύμβαση ότι εξακολουθούμε να αναφερόμαστε στην συνεχή συνάρτηση) σε ένα ολοκλήρωμα της μορφής

εδώ τώρα θα δημιουργηθούν πολλά προβλήματα ,γιατί πρέπει να το συμβολίσουμε:

προκειμένου να το υπολογίσουμε και κάτι τέτοιο δεν υπονοείτε στο βιβλίο (γενικευμένο ολοκλήρωμα β' είδους).
Ωστόσο αν σε μια πολύκλαδη συνάρτηση,π.χ.

με
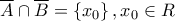
και

με την επιπλέον υπόθεση ότι οι τύποι των συναρτήσεων

ορίζονται στο κατ' επέκταση σημείο

.
Αν λοιπόν συνέβαιναν όλα τα παραπάνω θα μπορούσαμε να "σπάσουμε" το ολοκλήρωμα και να αντικαταστήσουμε τους επιμέρους κλειστούς τύπους.
π.χ.

Η συνάρτηση αυτή είναι συνεχής, ο αριθμός 2 ανήκει στις θήκες των συνόλων και ταυτόχρονα σε κάποιο απο τα δύο σύνολα. Ο τύπος της συνάρτησης που δεν περιέχει στο διάστημα που ορίζεται τον αριθμό 2, μπορεί να επεκταθεί σε αυτό ,ανάλογα και στον αριθμό 3.

και εδώ ισχύει αβίαστα το

.
Σε κάθε περίπτωση όμως βλέπω ότι συνολικά το θέμα είναι πολύ θεωρητικό και αναρωτιέμαι πόσοι μαθητές θα δικαιολογούσαν την ισότητα

επαρκώς.
Ρητορικά λοιπόν σαν μαθητής θα απαντούσα ότι προφανώς θα καταφύγουμε σε μια ισότητα συναρτήσεων όπως η προηγούμενη και επειδή ήδη θα έχουμε δείξει την συνέχεια δεν θα έχουμε και πολλά να πούμε γιατί είναι προφανές.

 .
. να έχει 4 διαφορετικές ρίζες.
να έχει 4 διαφορετικές ρίζες.
 συνεχής για
συνεχής για  (πράξεις μεταξύ συνεχών ) και εξετάζουμε στο
(πράξεις μεταξύ συνεχών ) και εξετάζουμε στο  και είναι
και είναι 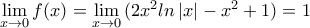 γιατί
γιατί  οπότε
οπότε  επομένως συνεχής και στο
επομένως συνεχής και στο 
 και
και  με
με  και
και 
![[-1,\,\,0],\,\,[1,\,+\infty ) [-1,\,\,0],\,\,[1,\,+\infty )](/forum/ext/geomar/texintegr/latexrender/pictures/954fe416df7f9c32ad4b15735f1ffef1.png) και γνήσια φθίνουσα στα διαστήματα
και γνήσια φθίνουσα στα διαστήματα ![(-\infty ,\,\,-1],\,\,[0,\,\,1] (-\infty ,\,\,-1],\,\,[0,\,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/1fd99b640d43cf5beefca8c38a424b5d.png) έτσι έχουμε
έτσι έχουμε ![f([-1,\,\,0])=[f(-1),\,\,f(0)],\,\,\,f([1,\,+\infty ))=[f(1),\,\,\underset{x\to +\infty }{\mathop{\lim }}\,f(x)) f([-1,\,\,0])=[f(-1),\,\,f(0)],\,\,\,f([1,\,+\infty ))=[f(1),\,\,\underset{x\to +\infty }{\mathop{\lim }}\,f(x))](/forum/ext/geomar/texintegr/latexrender/pictures/e5fcd5fa3a11c6d9d356feb57bd765af.png) ή
ή ![f([-1,\,\,0])=[0,\,\,1],\,\,\,f([1,\,+\infty ))=[0,\,\,+\infty ) f([-1,\,\,0])=[0,\,\,1],\,\,\,f([1,\,+\infty ))=[0,\,\,+\infty )](/forum/ext/geomar/texintegr/latexrender/pictures/7df57e95d79674d208ab70b6c4309e95.png) αφου
αφου 
![f((-\infty ,\,-1])=[f(-1),\,\,\underset{x\to -\infty }{\mathop{\lim }}\,f(x)),\,\,\,f([0,\,1])=[f(1),\,\,f(0)] f((-\infty ,\,-1])=[f(-1),\,\,\underset{x\to -\infty }{\mathop{\lim }}\,f(x)),\,\,\,f([0,\,1])=[f(1),\,\,f(0)]](/forum/ext/geomar/texintegr/latexrender/pictures/190b0505f81379a984b5a316561f586e.png) ή
ή ![f((-\infty ,\,-1])=[0,\,\,+\infty ),\,\,\,f([0,\,1])=[0,\,\,1] f((-\infty ,\,-1])=[0,\,\,+\infty ),\,\,\,f([0,\,1])=[0,\,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/60bdeb95623613fc7131ece05949eb10.png) άρα το σύνολο τιμών της
άρα το σύνολο τιμών της 
 με
με 


![(-\infty ,\,-\frac{1}{e}],\,\,[\frac{1}{e},\,+\infty ) (-\infty ,\,-\frac{1}{e}],\,\,[\frac{1}{e},\,+\infty )](/forum/ext/geomar/texintegr/latexrender/pictures/f102db8dc798e590770e13ae70484fd5.png) και κοίλη στα διαστήματα
και κοίλη στα διαστήματα ![[-\frac{1}{e},\,0],\,\,[0,\,\,\frac{1}{e}] [-\frac{1}{e},\,0],\,\,[0,\,\,\frac{1}{e}]](/forum/ext/geomar/texintegr/latexrender/pictures/09bc24984344ff1de3acba054137f67e.png)

![[-\frac{1}{e},\,\,\frac{1}{e}] [-\frac{1}{e},\,\,\frac{1}{e}]](/forum/ext/geomar/texintegr/latexrender/pictures/18023b1b560c8f18a306d75f5b8265ba.png)
 είναι άρτια.
είναι άρτια.
 η εξίσωση
η εξίσωση 
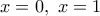 και του
και του  και θα το διπλασιάσουμε, έτσι τότε
και θα το διπλασιάσουμε, έτσι τότε 
 χρειάζεται παραγοντική βρίσκοντας το αόριστο ολοκλήρωμα ή με την χρήση της συνάρτησης ολοκλήρωμα αφού αν
χρειάζεται παραγοντική βρίσκοντας το αόριστο ολοκλήρωμα ή με την χρήση της συνάρτησης ολοκλήρωμα αφού αν  μία αρχική της έχουμε
μία αρχική της έχουμε
![=\left[ \frac{2}{3}{{t}^{3}}\ln t \right]_{1}^{x}-\frac{2}{3}\int\limits_{1}^{x}{({{t}^{3}}\frac{1}{t})dt-}\left[ \frac{1}{3}{{t}^{3}}-t \right]_{1}^{x}=\frac{2}{3}{{x}^{3}}\ln x-\frac{2}{3}\int\limits_{1}^{x}{({{t}^{2}})dt-}\frac{1}{3}{{x}^{3}}+t+\frac{2}{3} =\left[ \frac{2}{3}{{t}^{3}}\ln t \right]_{1}^{x}-\frac{2}{3}\int\limits_{1}^{x}{({{t}^{3}}\frac{1}{t})dt-}\left[ \frac{1}{3}{{t}^{3}}-t \right]_{1}^{x}=\frac{2}{3}{{x}^{3}}\ln x-\frac{2}{3}\int\limits_{1}^{x}{({{t}^{2}})dt-}\frac{1}{3}{{x}^{3}}+t+\frac{2}{3}](/forum/ext/geomar/texintegr/latexrender/pictures/653d86e34cb89771f108ca6d79027b15.png)
 έτσι τώρα θεωρώντας την
έτσι τώρα θεωρώντας την 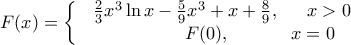 για να είναι αρχική της
για να είναι αρχική της 
 )
) 
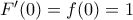 και έτσι για την παραπάνω
και έτσι για την παραπάνω 

![E=\int\limits_{0}^{1}{f(x)dx}=\left[ F(x) \right]_{0}^{1}=F(1)-F(0)=\frac{4}{9} E=\int\limits_{0}^{1}{f(x)dx}=\left[ F(x) \right]_{0}^{1}=F(1)-F(0)=\frac{4}{9}](/forum/ext/geomar/texintegr/latexrender/pictures/8706790d60821a48915785ae09ca11f4.png) και το ζητούμενο τελικά είναι
και το ζητούμενο τελικά είναι 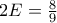
 χωρίς τη χρήση της αρχικής που κατασκεύασε και δικαιολόγησε ο συνάδελφος στην παραπάνω λύση και με χρήση βασικών μεθόδων ολοκλήρωσης (που είναι μέσα στη σχολική ύλη) να καταλήξουμε στο ίδιο αποτέλεσμα.
χωρίς τη χρήση της αρχικής που κατασκεύασε και δικαιολόγησε ο συνάδελφος στην παραπάνω λύση και με χρήση βασικών μεθόδων ολοκλήρωσης (που είναι μέσα στη σχολική ύλη) να καταλήξουμε στο ίδιο αποτέλεσμα. και τα δύο έχουν νόημα επειδή η συνάρτηση είναι συνεχής.
και τα δύο έχουν νόημα επειδή η συνάρτηση είναι συνεχής. εδώ τώρα θα δημιουργηθούν πολλά προβλήματα ,γιατί πρέπει να το συμβολίσουμε:
εδώ τώρα θα δημιουργηθούν πολλά προβλήματα ,γιατί πρέπει να το συμβολίσουμε:  προκειμένου να το υπολογίσουμε και κάτι τέτοιο δεν υπονοείτε στο βιβλίο (γενικευμένο ολοκλήρωμα β' είδους).
προκειμένου να το υπολογίσουμε και κάτι τέτοιο δεν υπονοείτε στο βιβλίο (γενικευμένο ολοκλήρωμα β' είδους). με
με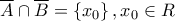 και
και  με την επιπλέον υπόθεση ότι οι τύποι των συναρτήσεων
με την επιπλέον υπόθεση ότι οι τύποι των συναρτήσεων  ορίζονται στο κατ' επέκταση σημείο
ορίζονται στο κατ' επέκταση σημείο  .
.

 .
. επαρκώς.
επαρκώς.  .
. και
και  που μας χρειάζονται για να υπολογίσουμε το ορισμένο ολοκλήρωμα που θα μας δώσει το εμβαδόν του χωρίου, δε χρειάζεται να υπολογίσουμε τον αριθμό
που μας χρειάζονται για να υπολογίσουμε το ορισμένο ολοκλήρωμα που θα μας δώσει το εμβαδόν του χωρίου, δε χρειάζεται να υπολογίσουμε τον αριθμό  (ο οποίος βέβαια μπορεί να υπολογισθεί όπως ήδη μας έχει γράψει στη λύση του ο Βασίλης). Οπότε υπολογίζοντας με χρήση βασικών μεθόδων το ολοκλήρωμα, βρίσκουμε ουσιαστικά τον τύπο της αρχικής που μας χρειάζεται, ώστε να υπολογίσουμε τους αριθμούς
(ο οποίος βέβαια μπορεί να υπολογισθεί όπως ήδη μας έχει γράψει στη λύση του ο Βασίλης). Οπότε υπολογίζοντας με χρήση βασικών μεθόδων το ολοκλήρωμα, βρίσκουμε ουσιαστικά τον τύπο της αρχικής που μας χρειάζεται, ώστε να υπολογίσουμε τους αριθμούς