Θα δείξουμε με επαγωγή τη γενίκευση:
Έστω μια διάταξη των αριθμών

. Σε κάθε βήμα, αν

είναι ο πρώτος αριθμός τότε αναδιατάσσουμε με αντίστροφη σειρά τους πρώτους

αριθμούς. Ισχύει ότι κάποια στιγμή ο αριθμός

θα βρεθεί στην πρώτη θέση και επομένως η διαδικασία θα σταματήσει.
Θεωρούμε ότι αρχικά ο πρώτος αριθμός δεν είναι το

αλλιώς η διαδικασία δεν θα αρχίσει καν.
Αν

, δηλαδή αν έχουμε τη διάταξη

τότε η διαδικασία ολοκληρώνεται μετά από

βήμα.
Αν

, τότε ας εξετάσουμε τις παρακάτω διατάξεις:

η διαδικασία ολοκληρώνεται μετά από

βήμα

η διαδικασία ολοκληρώνεται μετά από

βήματα

η διαδικασία ολοκληρώνεται μετά από

βήματα
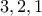
η διαδικασία ολοκληρώνεται μετά από

βήμα
Έστω ότι ισχύει για

ότι η διαδικασία κάποια στιγμή θα σταματήσει.
Θα αποδείξουμε ότι το ίδιο θα γίνει και για

.
Αν αρχικά ο αριθμός

βρίσκεται στην τελευταία θέση, τότε στις πρώτες

θέσεις βρίσκονται με κάποια διάταξη οι αριθμοί

έως

, οπότε ισχύει ότι η διαδικασία κάποια στιγμή θα σταματήσει.
Αν αρχικά ο αριθμός

δεν βρίσκεται στην τελευταία θέση, τότε αν σε κάποιο βήμα βρεθεί στην πρώτη θέση, τότε στο αμέσως επόμενο βήμα θα βρεθεί στην τελευταία θέση, όπου είδαμε ότι τότε η διαδικασία κάποια στιγμή θα σταματήσει.
Αν αρχικά ο αριθμός

δεν βρίσκεται στην τελευταία θέση, και σε κανένα βήμα δεν βρεθεί στην πρώτη θέση, τότε εφαρμόζουμε το εξής: Έστω

ο αριθμός που αρχικά βρίσκεται στην τελευταία θέση (παρατηρούμε ότι αυτός δεν αλλάζει σε κανένα από τα βήματα). Η διαδικασία δεν επηρεάζεται αν αντιμεταθέσουμε τον αριθμό

με τον αριθμό

, αφού τότε και ο

σε κανένα βήμα δεν θα βρεθεί στην πρώτη θέση. Έτσι όμως ο αριθμός

θα βρίσκεται στην τελευταία θέση, όπου είδαμε ότι τότε η διαδικασία κάποια στιγμή θα σταματήσει.
 φύλλα της τράπουλας
φύλλα της τράπουλας  με αντίστοιχες αξίες
με αντίστοιχες αξίες  Τα ανακατεύουμε και κοιτάμε το πρώτο. Αν η αξία του είναι
Τα ανακατεύουμε και κοιτάμε το πρώτο. Αν η αξία του είναι  τότε
τότε  πρώτα φύλλα και επαναλαμβάνουμε τη διαδικασία. Η διαδικασία τερματίζεται προφανώς αν
πρώτα φύλλα και επαναλαμβάνουμε τη διαδικασία. Η διαδικασία τερματίζεται προφανώς αν . Να αποδειχθεί ότι η διαδικασία δεν πρόκειται να πέσει σε αέναο κύκλο
. Να αποδειχθεί ότι η διαδικασία δεν πρόκειται να πέσει σε αέναο κύκλο .
. η οποία μετά την πρώτη αντιμετάθεση θα γίνει
η οποία μετά την πρώτη αντιμετάθεση θα γίνει  και στη δεύτερη τερματίζει.
και στη δεύτερη τερματίζει.
 . Σε κάθε βήμα, αν
. Σε κάθε βήμα, αν  θα βρεθεί στην πρώτη θέση και επομένως η διαδικασία θα σταματήσει.
θα βρεθεί στην πρώτη θέση και επομένως η διαδικασία θα σταματήσει. , δηλαδή αν έχουμε τη διάταξη
, δηλαδή αν έχουμε τη διάταξη  τότε η διαδικασία ολοκληρώνεται μετά από
τότε η διαδικασία ολοκληρώνεται μετά από  , τότε ας εξετάσουμε τις παρακάτω διατάξεις:
, τότε ας εξετάσουμε τις παρακάτω διατάξεις: η διαδικασία ολοκληρώνεται μετά από
η διαδικασία ολοκληρώνεται μετά από  η διαδικασία ολοκληρώνεται μετά από
η διαδικασία ολοκληρώνεται μετά από  βήματα
βήματα η διαδικασία ολοκληρώνεται μετά από
η διαδικασία ολοκληρώνεται μετά από 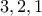 η διαδικασία ολοκληρώνεται μετά από
η διαδικασία ολοκληρώνεται μετά από  ότι η διαδικασία κάποια στιγμή θα σταματήσει.
ότι η διαδικασία κάποια στιγμή θα σταματήσει.  .
. βρίσκεται στην τελευταία θέση, τότε στις πρώτες
βρίσκεται στην τελευταία θέση, τότε στις πρώτες  θέσεις βρίσκονται με κάποια διάταξη οι αριθμοί
θέσεις βρίσκονται με κάποια διάταξη οι αριθμοί  ο αριθμός που αρχικά βρίσκεται στην τελευταία θέση (παρατηρούμε ότι αυτός δεν αλλάζει σε κανένα από τα βήματα). Η διαδικασία δεν επηρεάζεται αν αντιμεταθέσουμε τον αριθμό
ο αριθμός που αρχικά βρίσκεται στην τελευταία θέση (παρατηρούμε ότι αυτός δεν αλλάζει σε κανένα από τα βήματα). Η διαδικασία δεν επηρεάζεται αν αντιμεταθέσουμε τον αριθμό  . Ορίζουμε
. Ορίζουμε  το σύνολο όλων των χαρτιών τα οποία βρίσκονται στην θέση τους και ορίζουμε
το σύνολο όλων των χαρτιών τα οποία βρίσκονται στην θέση τους και ορίζουμε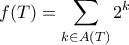
 αυξάνεται. Πράγματι αν το αρχικό χαρτί όταν κάνουμε την αντιμετάθεση είναι το
αυξάνεται. Πράγματι αν το αρχικό χαρτί όταν κάνουμε την αντιμετάθεση είναι το  , τότε το
, τότε το 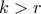 που ανήκει στο
που ανήκει στο  ανήκαν στο
ανήκαν στο  .
.