 φυσικός μεγαλύτερος του
φυσικός μεγαλύτερος του  . Γνωρίζουμε ότι ο
. Γνωρίζουμε ότι ο  έχει συνολικά
έχει συνολικά  διαιρέτες στο πλήθος. Να αποδειχθεί ότι το άθροισμα των διαιρετών του υπερβαίνει τον αριθμό
διαιρέτες στο πλήθος. Να αποδειχθεί ότι το άθροισμα των διαιρετών του υπερβαίνει τον αριθμό  .
.Συντονιστές: cretanman, silouan, rek2
 φυσικός μεγαλύτερος του
φυσικός μεγαλύτερος του  . Γνωρίζουμε ότι ο
. Γνωρίζουμε ότι ο  έχει συνολικά
έχει συνολικά  διαιρέτες στο πλήθος. Να αποδειχθεί ότι το άθροισμα των διαιρετών του υπερβαίνει τον αριθμό
διαιρέτες στο πλήθος. Να αποδειχθεί ότι το άθροισμα των διαιρετών του υπερβαίνει τον αριθμό  .
. διαιρέτες του
διαιρέτες του  ζευγαρώνονται σε
ζευγαρώνονται σε  ζεύγη όπου το γινόμενο του κάθε ζεύγους ισούται προς
ζεύγη όπου το γινόμενο του κάθε ζεύγους ισούται προς  . Για κάθε τέτοιο ζεύγος
. Για κάθε τέτοιο ζεύγος  ισχύει η
ισχύει η  . Για ένα ακριβώς από τα ζεύγη ισχύει η
. Για ένα ακριβώς από τα ζεύγη ισχύει η  , ενώ για τα υπόλοιπα
, ενώ για τα υπόλοιπα  ζεύγη ισχύει η
ζεύγη ισχύει η  (εκτός και αν ο
(εκτός και αν ο  είναι τέλειο τετράγωνο, οπότε έχει περιττό αριθμό διαιρετών, άτοπο). Συμπεραίνουμε ότι το άθροισμα των διαιρετών υπερβαίνει, εκτός και αν ο
είναι τέλειο τετράγωνο, οπότε έχει περιττό αριθμό διαιρετών, άτοπο). Συμπεραίνουμε ότι το άθροισμα των διαιρετών υπερβαίνει, εκτός και αν ο  είναι πρώτος (οπότε όλα απλοποιούνται καθώς
είναι πρώτος (οπότε όλα απλοποιούνται καθώς  ), τον
), τον  .
.Τα παραπάνω οδηγούν στην ακόλουθη εικασία (αν δεν είναι γνωστό αποτέλεσμα):gbaloglou έγραψε: ↑Δευ Μαρ 12, 2018 6:06 pmΒελτιώνοντας το ζητούμενο:
Παρατηρούμε ότι οιδιαιρέτες του
ζευγαρώνονται σε
ζεύγη όπου το γινόμενο του κάθε ζεύγους ισούται προς
. Για κάθε τέτοιο ζεύγος
ισχύει η
. Για ένα ακριβώς από τα ζεύγη ισχύει η
, ενώ για τα υπόλοιπα
ζεύγη ισχύει η
(εκτός και αν ο
είναι τέλειο τετράγωνο, οπότε έχει περιττό αριθμό διαιρετών, άτοπο). Συμπεραίνουμε ότι το άθροισμα των διαιρετών υπερβαίνει, εκτός και αν ο
είναι πρώτος (οπότε όλα απλοποιούνται καθώς
), τον
.
 ισούται προς το άθροισμα των αριθμών
ισούται προς το άθροισμα των αριθμών  , όπου
, όπου  ΚΑΙ
ΚΑΙ  τέλειο τετράγωνο.
τέλειο τετράγωνο. είναι πρώτος αν και μόνον αν ο μόνος φυσικός αριθμός
είναι πρώτος αν και μόνον αν ο μόνος φυσικός αριθμός  μικρότερος του
μικρότερος του  για τον οποίο ο
για τον οποίο ο  είναι τέλειο τετράγωνο είναι ο
είναι τέλειο τετράγωνο είναι ο  . Ένα βήμα πιο πέρα, ο
. Ένα βήμα πιο πέρα, ο  είναι γινόμενο δύο πρώτων αν και μόνον αν υπάρχουν δύο ακριβώς
είναι γινόμενο δύο πρώτων αν και μόνον αν υπάρχουν δύο ακριβώς  μικρότεροι του
μικρότεροι του  φυσικοί για τους οποίους ο
φυσικοί για τους οποίους ο  είναι τέλειο τετράγωνο, γινόμενο τριών πρώτων αν και μόνον αν υπάρχουν τέσσερις τέτοιοι
είναι τέλειο τετράγωνο, γινόμενο τριών πρώτων αν και μόνον αν υπάρχουν τέσσερις τέτοιοι  , κοκ (Στην περίπτωση
, κοκ (Στην περίπτωση  οι δύο 'αναζητούμενοι' αριθμοί είναι ο γνωστός ύποπτος
οι δύο 'αναζητούμενοι' αριθμοί είναι ο γνωστός ύποπτος  και ο
και ο  , από εκεί και πέρα μπλέκουν τα πράγματα (αλλά η εικασία φαίνεται να ισχύει ακόμη, πχ για
, από εκεί και πέρα μπλέκουν τα πράγματα (αλλά η εικασία φαίνεται να ισχύει ακόμη, πχ για  το άθροισμα των διαιρετών είναι
το άθροισμα των διαιρετών είναι  ).]
).]Δεν είναι και τόσο μυστηριώδες τελικά:gbaloglou έγραψε: ↑Τρί Μαρ 13, 2018 12:35 amΤα παραπάνω οδηγούν στην ακόλουθη εικασία (αν δεν είναι γνωστό αποτέλεσμα):gbaloglou έγραψε: ↑Δευ Μαρ 12, 2018 6:06 pmΒελτιώνοντας το ζητούμενο:
Παρατηρούμε ότι οιδιαιρέτες του
ζευγαρώνονται σε
ζεύγη όπου το γινόμενο του κάθε ζεύγους ισούται προς
. Για κάθε τέτοιο ζεύγος
ισχύει η
. Για ένα ακριβώς από τα ζεύγη ισχύει η
, ενώ για τα υπόλοιπα
ζεύγη ισχύει η
(εκτός και αν ο
είναι τέλειο τετράγωνο, οπότε έχει περιττό αριθμό διαιρετών, άτοπο). Συμπεραίνουμε ότι το άθροισμα των διαιρετών υπερβαίνει, εκτός και αν ο
είναι πρώτος (οπότε όλα απλοποιούνται καθώς
), τον
.
Το άθροισμα των διαιρετών τουισούται προς το άθροισμα των αριθμών
, όπου
ΚΑΙ
τέλειο τετράγωνο.
[Ως ειδική περίπτωση, οείναι πρώτος αν και μόνον αν ο μόνος φυσικός αριθμός
μικρότερος του
για τον οποίο ο
είναι τέλειο τετράγωνο είναι ο
. Ένα βήμα πιο πέρα, ο
είναι γινόμενο δύο πρώτων αν και μόνον αν υπάρχουν δύο ακριβώς
μικρότεροι του
φυσικοί για τους οποίους ο
είναι τέλειο τετράγωνο, γινόμενο τριών πρώτων αν και μόνον αν υπάρχουν τέσσερις τέτοιοι
, κοκ (Στην περίπτωση
οι δύο 'αναζητούμενοι' αριθμοί είναι ο γνωστός ύποπτος
και ο
, από εκεί και πέρα μπλέκουν τα πράγματα (αλλά η εικασία φαίνεται να ισχύει ακόμη, πχ για
το άθροισμα των διαιρετών είναι
).]


Λέω και εγώ να γράψω την λύση μου...gbaloglou έγραψε: ↑Δευ Μαρ 12, 2018 6:06 pmΒελτιώνοντας το ζητούμενο:
Παρατηρούμε ότι οιδιαιρέτες του
ζευγαρώνονται σε
ζεύγη όπου το γινόμενο του κάθε ζεύγους ισούται προς
. Για κάθε τέτοιο ζεύγος
ισχύει η
. Για ένα ακριβώς από τα ζεύγη ισχύει η
, ενώ για τα υπόλοιπα
ζεύγη ισχύει η
(εκτός και αν ο
είναι τέλειο τετράγωνο, οπότε έχει περιττό αριθμό διαιρετών, άτοπο). Συμπεραίνουμε ότι το άθροισμα των διαιρετών υπερβαίνει, εκτός και αν ο
είναι πρώτος (οπότε όλα απλοποιούνται καθώς
), τον
.
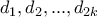 οι διαιρέτες του
οι διαιρέτες του 
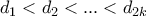 .Τότε προφανώς
.Τότε προφανώς 
 κλπ. μέχρι
κλπ. μέχρι  .Άρα το άθροισμα
.Άρα το άθροισμα  είναι ίσο με
είναι ίσο με  .Όμως, από την ανισότητα αριθμητικού-γεωμετρικού μεσου έχω για κάθε
.Όμως, από την ανισότητα αριθμητικού-γεωμετρικού μεσου έχω για κάθε 
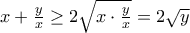 ,όπου η ισότητα ισχύει μόνο για
,όπου η ισότητα ισχύει μόνο για  .Έτσι, το άθροισμα μας είναι μεγαλύτερο ή ίσο του
.Έτσι, το άθροισμα μας είναι μεγαλύτερο ή ίσο του 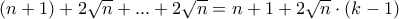 , αφόυ ο όρος
, αφόυ ο όρος 
 φορές.Αλλά για να ισχύει η ισότητα πρέπει
φορές.Αλλά για να ισχύει η ισότητα πρέπει  , άτοπο αφού εάν ο n είναι τέλειο τετράγωνο τότε έχει περιττό πλήθος διαιρετών.Άρα
, άτοπο αφού εάν ο n είναι τέλειο τετράγωνο τότε έχει περιττό πλήθος διαιρετών.Άρα 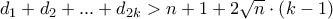
 , οπότε
, οπότε  .Σύνεπώς, το ζητούμενο άθροισμα υπερβαίνει τον αριθμό
.Σύνεπώς, το ζητούμενο άθροισμα υπερβαίνει τον αριθμό  .Τέλος, παρατηρούμε οτί για κάθε
.Τέλος, παρατηρούμε οτί για κάθε  ισχύει
ισχύει  (εύκολη απόδειξη με χιαστί), επομένως
(εύκολη απόδειξη με χιαστί), επομένως 
Αγαπητέ glinos ως εδώ λέμε περίπου τα ίδια πράγματα, από εδώ και πέρα εξασθενείς ο ίδιος την ανισότητα (σου), πιστεύω δηλαδή ότι τα παρακάτω δεν χρειάζονται.glinos έγραψε: ↑Τρί Μαρ 13, 2018 4:59 pmΛέω και εγώ να γράψω την λύση μου...gbaloglou έγραψε: ↑Δευ Μαρ 12, 2018 6:06 pmΒελτιώνοντας το ζητούμενο:
Παρατηρούμε ότι οιδιαιρέτες του
ζευγαρώνονται σε
ζεύγη όπου το γινόμενο του κάθε ζεύγους ισούται προς
. Για κάθε τέτοιο ζεύγος
ισχύει η
. Για ένα ακριβώς από τα ζεύγη ισχύει η
, ενώ για τα υπόλοιπα
ζεύγη ισχύει η
(εκτός και αν ο
είναι τέλειο τετράγωνο, οπότε έχει περιττό αριθμό διαιρετών, άτοπο). Συμπεραίνουμε ότι το άθροισμα των διαιρετών υπερβαίνει, εκτός και αν ο
είναι πρώτος (οπότε όλα απλοποιούνται καθώς
), τον
.
Λοιπόν, έστωοι διαιρέτες του
με.Τότε προφανώς
καικλπ. μέχρι
.Άρα το άθροισμα
είναι ίσο με
.Όμως, από την ανισότητα αριθμητικού-γεωμετρικού μεσου έχω για κάθε
ότι,όπου η ισότητα ισχύει μόνο για
.Έτσι, το άθροισμα μας είναι μεγαλύτερο ή ίσο του
, αφόυ ο όρος
εμφανίζεται συνολικάφορές.Αλλά για να ισχύει η ισότητα πρέπει
, άτοπο αφού εάν ο n είναι τέλειο τετράγωνο τότε έχει περιττό πλήθος διαιρετών.Άρα
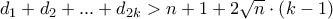
Τώρα από την ανισότητα γεωμετρικού-αρμονικού μέσου έχω, οπότε
.Σύνεπώς, το ζητούμενο άθροισμα υπερβαίνει τον αριθμό
.Τέλος, παρατηρούμε οτί για κάθε
ισχύει
(εύκολη απόδειξη με χιαστί), επομένως

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες