 να βρείτε:
να βρείτε:α) την αντίστροφή της
β) το πεδίο ορισμού της συνάρτησης

γ) το ελάχιστο της συνάρτησης

Συντονιστής: m.pαpαgrigorakis
 να βρείτε:
να βρείτε:

...μια ημιτελής νυχτερινή προσπάθεια....Παύλος Μαραγκουδάκης έγραψε: ↑Τρί Οκτ 17, 2017 11:23 pmΓια τη συνάρτησηνα βρείτε:
α) την αντίστροφή της
β) το πεδίο ορισμού της συνάρτησης

![{{e}^{3x}}+3{{e}^{2x}}+3{{e}^{x}}+1={{e}^{y}}+1\Leftrightarrow {{\left( {{e}^{x}}+1 \right)}^{3}}={{e}^{y}}+1\Leftrightarrow {{e}^{x}}+1=\sqrt[3]{{{e}^{y}}+1}\Leftrightarrow {{e}^{3x}}+3{{e}^{2x}}+3{{e}^{x}}+1={{e}^{y}}+1\Leftrightarrow {{\left( {{e}^{x}}+1 \right)}^{3}}={{e}^{y}}+1\Leftrightarrow {{e}^{x}}+1=\sqrt[3]{{{e}^{y}}+1}\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/0957329033f7802aa1eb0cda7827a93e.png)
![{{e}^{x}}=\sqrt[3]{{{e}^{y}}+1}-1\Leftrightarrow \left\{ \begin{matrix}
& \sqrt[3]{{{e}^{y}}+1}-1>0 \\
& x=\ln \left( \sqrt[3]{{{e}^{y}}+1}-1 \right) \\
\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}
& \sqrt[3]{{{e}^{y}}+1}>1 \\
& x=\ln \left( \sqrt[3]{{{e}^{y}}+1}-1 \right) \\
\end{matrix} \right. {{e}^{x}}=\sqrt[3]{{{e}^{y}}+1}-1\Leftrightarrow \left\{ \begin{matrix}
& \sqrt[3]{{{e}^{y}}+1}-1>0 \\
& x=\ln \left( \sqrt[3]{{{e}^{y}}+1}-1 \right) \\
\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}
& \sqrt[3]{{{e}^{y}}+1}>1 \\
& x=\ln \left( \sqrt[3]{{{e}^{y}}+1}-1 \right) \\
\end{matrix} \right.](/forum/ext/geomar/texintegr/latexrender/pictures/cde63227412bbb4946ed6a2563e33445.png)
![\Leftrightarrow \left\{ \begin{matrix}
& \sqrt[3]{{{e}^{y}}+1}>1 \\
& x=\ln \left( \sqrt[3]{{{e}^{y}}+1}-1 \right) \\
\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}
& {{e}^{y}}+1>1 \\
& x=\ln \left( \sqrt[3]{{{e}^{y}}+1}-1 \right) \\
\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}
& {{e}^{y}}>0 \\
& x=\ln \left( \sqrt[3]{{{e}^{y}}+1}-1 \right) \\
\end{matrix} \right. \Leftrightarrow \left\{ \begin{matrix}
& \sqrt[3]{{{e}^{y}}+1}>1 \\
& x=\ln \left( \sqrt[3]{{{e}^{y}}+1}-1 \right) \\
\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}
& {{e}^{y}}+1>1 \\
& x=\ln \left( \sqrt[3]{{{e}^{y}}+1}-1 \right) \\
\end{matrix} \right.\Leftrightarrow \left\{ \begin{matrix}
& {{e}^{y}}>0 \\
& x=\ln \left( \sqrt[3]{{{e}^{y}}+1}-1 \right) \\
\end{matrix} \right.](/forum/ext/geomar/texintegr/latexrender/pictures/c458b68028c26a101f99bfa4d12fcf81.png)
 και η εξίσωση έχει μοναδική λύση, η συνάρτηση είναι
και η εξίσωση έχει μοναδική λύση, η συνάρτηση είναι 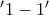
 με
με ![{{f}^{-1}}(x)=\ln \left( \sqrt[3]{{{e}^{x}}+1}-1 \right) {{f}^{-1}}(x)=\ln \left( \sqrt[3]{{{e}^{x}}+1}-1 \right)](/forum/ext/geomar/texintegr/latexrender/pictures/3f73eaeaadf52f11e469c53f41111105.png)
 πρέπει και αρκεί να υπάρχουν
πρέπει και αρκεί να υπάρχουν  ώστε
ώστε 
![\Leftrightarrow \ln ({{e}^{3x}}+3{{e}^{2x}}+3{{e}^{x}})>9\ln \left( \sqrt[3]{{{e}^{x}}+1}-1 \right)\Leftrightarrow \ln \left( {{({{e}^{x}}+1)}^{3}}-1 \right)>9\ln \left( \sqrt[3]{{{e}^{x}}+1}-1 \right) \Leftrightarrow \ln ({{e}^{3x}}+3{{e}^{2x}}+3{{e}^{x}})>9\ln \left( \sqrt[3]{{{e}^{x}}+1}-1 \right)\Leftrightarrow \ln \left( {{({{e}^{x}}+1)}^{3}}-1 \right)>9\ln \left( \sqrt[3]{{{e}^{x}}+1}-1 \right)](/forum/ext/geomar/texintegr/latexrender/pictures/c2978152102db6f6e493f907991fc55c.png)
![\sqrt[3]{{{e}^{x}}+1}-1=\kappa >0\Leftrightarrow \sqrt[3]{{{e}^{x}}+1}=\kappa +1\Leftrightarrow {{e}^{x}}+1={{(\kappa +1)}^{3}} \sqrt[3]{{{e}^{x}}+1}-1=\kappa >0\Leftrightarrow \sqrt[3]{{{e}^{x}}+1}=\kappa +1\Leftrightarrow {{e}^{x}}+1={{(\kappa +1)}^{3}}](/forum/ext/geomar/texintegr/latexrender/pictures/ce51255e1d4f915238dbe24cf2ab86a6.png)

 που είναι παραγωγίσιμη με
που είναι παραγωγίσιμη με  και
και 
 που σημαίνει ότι η
που σημαίνει ότι η 
 είναι
είναι  που σημαίνει ότι η
που σημαίνει ότι η  είναι γνήσια αύξουσα στο
είναι γνήσια αύξουσα στο 
 , επομένως η (1) ισχύει για κάθε
, επομένως η (1) ισχύει για κάθε 

 που γράφει πιο πάνω ο Βασίλης.
που γράφει πιο πάνω ο Βασίλης. και
και  , είναι
, είναι 

Πιο απλά, είναι σαφές από το ανάπτυγμα του διωνύμου ότιKAKABASBASILEIOS έγραψε: ↑Τετ Οκτ 18, 2017 12:46 am
...και για την τελευταία ψάχνω μια σύντομη διαδρομή...
...και αφού δεν βλέπω κάτι σύντομο...επέμβαση με άλλα όπλα...( παράνομα εκτός φακελλου...)
 από όπου το ζητούμενο είναι άμεσο.
από όπου το ζητούμενο είναι άμεσο.![(k+1)^9 = \left [(k+1)^3\right ] ^3 = (k^3+3k^2+3k+1)^3> (k^3+1)^3 = k^9+ 3k^6+3k^3+1 > k^9+1 (k+1)^9 = \left [(k+1)^3\right ] ^3 = (k^3+3k^2+3k+1)^3> (k^3+1)^3 = k^9+ 3k^6+3k^3+1 > k^9+1](/forum/ext/geomar/texintegr/latexrender/pictures/1ce1dd4332c59ee5bbc10c5bddf3506e.png)


 αποκτά τη μέγιστη τιμή της
αποκτά τη μέγιστη τιμή της Συμφωνώντας απόλυτα θα έλεγα και κάτι ακόμα: κάποια στιγμή πρέπει να μάθουν και την απόδειξη με επαγωγή. Η παραπάνω πρόταση στους θετικούς αποδεικνύεται εύκολα με επαγωγικό τρόπο επίσηςMihalis_Lambrou έγραψε: ↑Τετ Οκτ 18, 2017 9:37 amΠιο απλά, είναι σαφές από το ανάπτυγμα του διωνύμου ότιKAKABASBASILEIOS έγραψε: ↑Τετ Οκτ 18, 2017 12:46 am
...και για την τελευταία ψάχνω μια σύντομη διαδρομή...
...και αφού δεν βλέπω κάτι σύντομο...επέμβαση με άλλα όπλα...( παράνομα εκτός φακελλου...)
από όπου το ζητούμενο είναι άμεσο.
Αν θεωρούμε ότι ο μαθητής δεν μπορεί να χειριστεί έννατη δύναμη (*), μπορούμε να διεκπεραιώσουμε την άσκηση με χρήση τρίτης δύναμης (που την ξέρει) ως εξής. Θα πλατειάσω λίγο για να ... προσομοιώσω τον μαθητή:
![(k+1)^9 = \left [(k+1)^3\right ] ^3 = (k^3+3k^2+3k+1)^3> (k^3+1)^3 = k^9+ 3k^6+3k^3+1 > k^9+1 (k+1)^9 = \left [(k+1)^3\right ] ^3 = (k^3+3k^2+3k+1)^3> (k^3+1)^3 = k^9+ 3k^6+3k^3+1 > k^9+1](/forum/ext/geomar/texintegr/latexrender/pictures/1ce1dd4332c59ee5bbc10c5bddf3506e.png)
και λοιπά.
(*) Εδώ φαίνεται άλλη μια φορά ένα από τα δράματα της Μαθηματικής Παιδείας που παρέχουμε στην χώρα μας: Ο μαθητής ξέρει το θεώρημα Bolzano, το Rolle, l' Hospital, ολοκήρωση, κάποιες διαφορικές εξισώσεις και άλλα τόσα, αλλά αγνοεί βασικά πράγματα όπως το ανάπτυγμα του διωνύμου. Και μετά αναρωτιώμαστε "τις πταίει". Παρατηρώ τον μέσο φοιτητή και με θλίψη διαπιστώνω ότι ξέρει ελάχιστα πράγματα και αυτά με τεράστια σύγχυση στο μυαλό του.
 ή
ή για κάθε
για κάθε  οπότε
οπότε ή
ή και τελικά
και τελικά για κάθε
για κάθε 




 παίρνει ελάχιστη τιμή όταν
παίρνει ελάχιστη τιμή όταν 
 είναι το
είναι το  και το παίρνει όταν
και το παίρνει όταν 


Ένα τυπογραφικό :ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Πέμ Οκτ 19, 2017 5:50 pm
Θεωρούμε την
Είναι
Οι ρίζες της παραγώγου είναι τα
Αφου



 και επιτυγχάνεται όταν
και επιτυγχάνεται όταν  (Η τελευταία έχει ακριβώς δύο λύσεις αφού η
(Η τελευταία έχει ακριβώς δύο λύσεις αφού η  είναι 1-1 και έχει σύνολο τιμών όλο το
είναι 1-1 και έχει σύνολο τιμών όλο το  )
) ώστε η συνάρτηση
ώστε η συνάρτηση  να έχει πεδίο ορισμού όλο το
να έχει πεδίο ορισμού όλο το 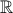 ;
;



 παίρνει ελάχιστη τιμή όταν
παίρνει ελάχιστη τιμή όταν  η
η 
 είναι το
είναι το 
 η
η 
 η
η 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες