 του σχήματος είναι
του σχήματος είναι  και
και  Να δείξετε ότι
Να δείξετε ότι 
Συντονιστής: chris_gatos
 Έστω
Έστω  , τότε
, τότε 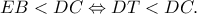
 ή
ή  ,
,  Όμως η
Όμως η  είναι άτοπο. Όμοια αν υποθέσουμε
είναι άτοπο. Όμοια αν υποθέσουμε 
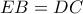 που μας οδηγεί άμεσα στην
που μας οδηγεί άμεσα στην 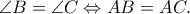
S.E.Louridas έγραψε: ↑Σάβ Σεπ 23, 2017 10:46 pmΕντάξει Γιώργο.
Αλλάζω την απόδειξη και θα επανέλθω για να το αποδείξω όπως αρχικά είχα σκεφτεί δηλαδή με ταυτόσημα βήματα όπως εκείνα του:
"Αν οι διχοτόμοι τριγώνου είναι ίσες, τότε, αυτό είναι ισοσκελές". Απλά ήθελα να κάνω μία υπέρβαση με τους κύκλους, ιδέα που με δελέασε...
Αρχικά θεωρούμε το παραλληλόγραμμοΈστω
, τότε
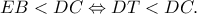
Παρατηρούμε ότιή
,
καθότιΌμως η
είναι άτοπο. Όμοια αν υποθέσουμε

θα καταλήξουμε και πάλι σε άτοπο. Συνεπώςπου μας οδηγεί άμεσα στην
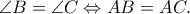
Από τον Νόμο των ημιτόνων στα
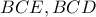 έχουμε
έχουμε  .
.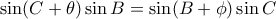 , οπότε
, οπότε  ή αλλιώς
ή αλλιώς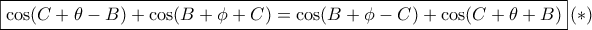 .
. (όμοια η ανάποδη περίπτωση). Τότε
(όμοια η ανάποδη περίπτωση). Τότε  , άρα
, άρα 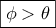 . Όμοια
. Όμοια  .
.  (ισοδυναμεί με την αληθή
(ισοδυναμεί με την αληθή 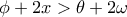 ) και
) και  .
.  και
και  που με πρόσθεση κατά μέλη έρχεται σε αντίφαση με την
που με πρόσθεση κατά μέλη έρχεται σε αντίφαση με την  . Άτοπο.
. Άτοπο. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης