 έτσι ώστε ο
έτσι ώστε ο  να είναι φυσικός.
να είναι φυσικός.Συντονιστές: achilleas, emouroukos, silouan
 έτσι ώστε ο
έτσι ώστε ο  να είναι φυσικός.
να είναι φυσικός. και άρα
και άρα  .
.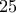 modulo
modulo  . Τρέχω πρώτα τον Ευκλείδειο αλγόριθμο για να βρω τον μέγιστο κοινό διαιρέτη των
. Τρέχω πρώτα τον Ευκλείδειο αλγόριθμο για να βρω τον μέγιστο κοινό διαιρέτη των  και
και 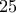 . Οι πρώτες δυο γραμμές είναι
. Οι πρώτες δυο γραμμές είναι 
 και συνεχίζω τρέχοντας τον Ευκλείδιο αλγόριθμο ανάποδα:
και συνεχίζω τρέχοντας τον Ευκλείδιο αλγόριθμο ανάποδα:


 . Επιτρέπονται επειδή
. Επιτρέπονται επειδή  .]
.] . Άρα
. Άρα  .
. . Άρα
. Άρα
 .
.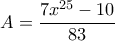 . Αφού
. Αφού 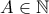 , είναι και
, είναι και  , οπότε
, οπότε  .
. (1).
(1). (2).
(2). (3).
(3). , είναι
, είναι  , άτοπο, οπότε
, άτοπο, οπότε  .
. , και
, και

 , οπότε
, οπότε  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες