 υπάρχουν άπειροι αριθμοί
υπάρχουν άπειροι αριθμοί  ώστε ο μεγαλύτερος πρώτος διαιρέτης του
ώστε ο μεγαλύτερος πρώτος διαιρέτης του 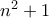 να είναι μεγαλύτερος του
να είναι μεγαλύτερος του 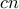 .
.Συντονιστές: cretanman, silouan, rek2
 υπάρχουν άπειροι αριθμοί
υπάρχουν άπειροι αριθμοί  ώστε ο μεγαλύτερος πρώτος διαιρέτης του
ώστε ο μεγαλύτερος πρώτος διαιρέτης του 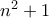 να είναι μεγαλύτερος του
να είναι μεγαλύτερος του 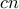 .
. ο iοστός πρώτος αριθμός.
ο iοστός πρώτος αριθμός. ο ελάχιστος πρώτος που είναι μεγαλύτερος από
ο ελάχιστος πρώτος που είναι μεγαλύτερος από 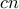 τότε ο αριθμός
τότε ο αριθμός ικανοποιεί το ζητούμενο για κάθε ακέραιο
ικανοποιεί το ζητούμενο για κάθε ακέραιο 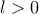 .
.Μάλλον κάπου κάνεις λάθος. Ορίζεις τοΤροβαδούρος έγραψε:Έστωο iοστός πρώτος αριθμός.
Έστωο ελάχιστος πρώτος που είναι μεγαλύτερος από
τότε ο αριθμός
ικανοποιεί το ζητούμενο για κάθε ακέραιο
.
Δε μου φαίνεται να ανήκει σε αυτό το φάκελο.
 χρησιμοποιώντας το
χρησιμοποιώντας το  και μετά ορίζεις το
και μετά ορίζεις το  χρησιμοποιώντας το
χρησιμοποιώντας το 
Υπάρχει πρόβλημα με την εκφώνηση. Μάλλον πρέπει να λέει « ... ο μεγαλύτερος πρώτος διαιρέτης ... »WLOG έγραψε:Να αποδείξετε ότι για κάθευπάρχουν άπειροι αριθμοί
ώστε ο μεγαλύτερος διαιρέτης του
να είναι μεγαλύτερος του
.
Ναι έχετε δίκιο έκανα λάθος μετάφραση!!Demetres έγραψε:Μάλλον κάπου κάνεις λάθος. Ορίζεις τοΤροβαδούρος έγραψε:Έστωο iοστός πρώτος αριθμός.
Έστωο ελάχιστος πρώτος που είναι μεγαλύτερος από
τότε ο αριθμός
ικανοποιεί το ζητούμενο για κάθε ακέραιο
.
Δε μου φαίνεται να ανήκει σε αυτό το φάκελο.χρησιμοποιώντας το
και μετά ορίζεις το
χρησιμοποιώντας το
Υπάρχει πρόβλημα με την εκφώνηση. Μάλλον πρέπει να λέει « ... ο μεγαλύτερος πρώτος διαιρέτης ... »WLOG έγραψε:Να αποδείξετε ότι για κάθευπάρχουν άπειροι αριθμοί
ώστε ο μεγαλύτερος διαιρέτης του
να είναι μεγαλύτερος του
.
WLOG έγραψε:Να αποδείξετε ότι για κάθευπάρχουν άπειροι αριθμοί
ώστε ο μεγαλύτερος πρώτος διαιρέτης του
να είναι μεγαλύτερος του
.
 ώστε ο
ώστε ο  να έχει πρώτο διαιρέτη μεγαλύτερο από
να έχει πρώτο διαιρέτη μεγαλύτερο από  .
.Έστωsilouan έγραψε:Ας δείξουμε πρώτα το ευκολότερο:
Υπάρχουν άπειροιώστε ο
να έχει πρώτο διαιρέτη μεγαλύτερο από
.
 πρώτος. Γνωρίζουμε ότι υπάρχει
πρώτος. Γνωρίζουμε ότι υπάρχει  ώστε
ώστε  . Επιπλέον στο διάστημα
. Επιπλέον στο διάστημα  υπάρχουν ακριβώς δύο τέτοια
υπάρχουν ακριβώς δύο τέτοια  . Το άθροισμά τους ισούται με
. Το άθροισμά τους ισούται με  οπότε μπορούμε να υποθέσουμε πως αυτά είναι τα
οπότε μπορούμε να υποθέσουμε πως αυτά είναι τα  και το
και το  για κάποιο
για κάποιο  .
.  . Από την επιλογή του
. Από την επιλογή του  , ο
, ο  διαιρεί τον
διαιρεί τον  . Επιπλέον, αφού
. Επιπλέον, αφού  τότε
τότε
 είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  οπότε
οπότε  εκτός και αν
εκτός και αν  το οποίο μπορεί να συμβεί μόνο για αρκετά μικρό
το οποίο μπορεί να συμβεί μόνο για αρκετά μικρό  .
.
 .
.Μου φαίνεται ότι πρέπει να χρησιμοποιηθούν βαριά όπλαDemetres έγραψε:Μου φαίνεται εύκολο για πρόβλημα 3. Ιδίως για σχετικά πρόσφατη ολυμπιάδα.
Από την άλλη το αρχικό πρόβλημα φαίνεται εξαιρετικά δύσκολο. Έχω μια ιδέα η οποία πρέπει να δουλεύει αλλά θέλει θεώρημα πρώτων αριθμών και μάλιστα με μη τετριμμένο τρόπο. Γνωρίζουμε αν το πρόβλημα έχει πιο στοιχειώδη λύση ή αν χρειάζονται τα βαρέα όπλα;
 .
. όπου
όπου  είναι η μεγαλύτερη δύναμη του πρώτου
είναι η μεγαλύτερη δύναμη του πρώτου  η οποία διαιρεί το
η οποία διαιρεί το  . Επομένως
. Επομένως  .
. Παρατηρούμε τα εξής:
Παρατηρούμε τα εξής: για
για  αφού αν
αφού αν  και
και  τότε
τότε 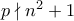 .
. αφού
αφού 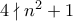 και επιπλέον
και επιπλέον  περιττός.
περιττός. για
για  .
. με
με  τότε υπάρχουν δύο υπόλοιπα
τότε υπάρχουν δύο υπόλοιπα 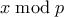 ώστε
ώστε 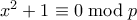 . Από το Λήμμα Hensel (
. Από το Λήμμα Hensel ( τότε
τότε  για
για  ) για κάθε
) για κάθε  υπάρχουν δύο υπόλοιπα
υπάρχουν δύο υπόλοιπα  ώστε
ώστε  . Άρα για αυτά τα
. Άρα για αυτά τα  έχουμε
έχουμε 
 είναι μέγιστο ώστε
είναι μέγιστο ώστε  .
.
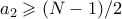 , άρα
, άρα  .
. 
 το πλήθος των πρώτων της μορφής
το πλήθος των πρώτων της μορφής  που είναι μικρότεροι ή ίσοι του
που είναι μικρότεροι ή ίσοι του  . Στην τελευταία ανισότητα χρησιμοποιήσαμε ότι
. Στην τελευταία ανισότητα χρησιμοποιήσαμε ότι  οπότε η ανισότητα ισχύει άνετα για αρκετά μεγάλα
οπότε η ανισότητα ισχύει άνετα για αρκετά μεγάλα 
 βλέπουμε ότι
βλέπουμε ότι 

 όπου το άθροισμα είναι σε όλους τους πρώτους
όπου το άθροισμα είναι σε όλους τους πρώτους  της μορφής
της μορφής  .
.  .
.
 όπου
όπου  το πλήθος των πρώτων για τους οποίους
το πλήθος των πρώτων για τους οποίους  . Δηλαδή αυτούς για τους οποίους υπάρχει
. Δηλαδή αυτούς για τους οποίους υπάρχει  με
με  .
.  που δίνει
που δίνει  .
. θα έχουμε τουλάχιστον
θα έχουμε τουλάχιστον  τόσους πρώτους. Μέχρι όμως το
τόσους πρώτους. Μέχρι όμως το  έχουμε το πολύ
έχουμε το πολύ  πρώτους αριθμούς.
πρώτους αριθμούς. πρώτους μεγαλύτερους του
πρώτους μεγαλύτερους του  ώστε κάθε ένας να διαιρεί το
ώστε κάθε ένας να διαιρεί το  για κάποιο
για κάποιο  .
.Υπάρχουν άπειροι φυσικοί αριθμοί
 για τους οποίους ο αριθμός
για τους οποίους ο αριθμός  έχει έναν πρώτο δειερετη μεγαλύτερο τού
έχει έναν πρώτο δειερετη μεγαλύτερο τού .
.Η απόδειξη αφήνεται λόγω απλότητας ως άσκηση για τον αναγνώστη. ( https://arxiv.org/abs/1908.08816 )
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 11 επισκέπτες