ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 1363: Να λυθεί στο N η εξίσωση:
Μ'αρέσει πολύ!!! Πολύ ωραία άσκηση για τα παιδιά!!! Ακούνε Ορέστης, Νικόλας, jimnt, Χάρης και Διονύσης?
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 1363: Να λυθεί στο N η εξίσωση:
Καλησπέρα κύριε Δημήτρη!ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 1363: Να λυθεί στο N η εξίσωση:
 ,
,  .
. , άρα
, άρα  , οπότε
, οπότε 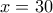 .
. .
. ,
,  , οπότε
, οπότε  .
. .
.
ΜΠΡΑΒΟ για την παρατήρηση. Διόρθωσα το τυπογραφικό λάθος.JimNt. έγραψε:Η εκφώνηση νομίζω είναι λάθος. Κάθε ρίζα είναι μεγαλύτερη της μονάδας...
Καλησπέρα!ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 1364: Να αποδείξετε ότι:
 .
. και πρόσθεση παίρνουμε
και πρόσθεση παίρνουμε  ο.ε.δ.
ο.ε.δ. ,
,  ,
,  και
και  να δείξετε ότι
να δείξετε ότι 
Από την σχέσηΚατερινόπουλος Νικόλας έγραψε:ΑΣΚΗΣΗ 1365 Αν,
,
και
να δείξετε ότι
 παίρνουμε
παίρνουμε  , οπότε
, οπότε
 ο.ε.δ.
ο.ε.δ.Πολύ ωραίος Ορέστη!! Ύπάρχει και πιο σύντομη λύση και μάλιστα πολύ ωραία νομίζω!! Για να την κοιτάξουμε λίγο ακόμη!!Ορέστης Λιγνός έγραψε:Από την σχέσηΚατερινόπουλος Νικόλας έγραψε:ΑΣΚΗΣΗ 1365 Αν,
,
και
να δείξετε ότι
παίρνουμε
, οπότε
ο.ε.δ.
Καλημέρα κύριε Νίκο.Τσιαλας Νικολαος έγραψε:Πολύ ωραίος Ορέστη!! Ύπάρχει και πιο σύντομη λύση και μάλιστα πολύ ωραία νομίζω!! Για να την κοιτάξουμε λίγο ακόμη!!Ορέστης Λιγνός έγραψε:Από την σχέσηΚατερινόπουλος Νικόλας έγραψε:ΑΣΚΗΣΗ 1365 Αν,
,
και
να δείξετε ότι
παίρνουμε
, οπότε
ο.ε.δ.


 ελαστικών ενός καινούριου αυτοκινήτου (
ελαστικών ενός καινούριου αυτοκινήτου ( στους τροχούς και
στους τροχούς και  για ρεζέρβα)
για ρεζέρβα)  που διανύει συνολικά το αυτοκίνητο. Για πόσα
που διανύει συνολικά το αυτοκίνητο. Για πόσα  πρέπει να
πρέπει να Κατερινόπουλος Νικόλας έγραψε:Άσκηση 1366
Ας υποθέσουμε ότι για τη χρήσηελαστικών ενός καινούριου αυτοκινήτου (
στους τροχούς και
για ρεζέρβα)
πρέπει κανείς να τα χρησιμοποιεί ομοιόμορφα για κάθεπου διανύει συνολικά το αυτοκίνητο. Για πόσα
πρέπει να
χρησιμοποιηθεί συνολικά το κάθε λάστιχο; Πώς μπορεί να το πετύχει αυτό ο οδηγός;
Αφιερωμένη στον Ορέστη!
Για τοΚατερινόπουλος Νικόλας έγραψε:Άσκηση 1367
Να συγκρίνετε τους αριθμούς:
και
 έχουμε
έχουμε  περιττές δυνάμεις. Οπότε
περιττές δυνάμεις. Οπότε  . Για το
. Για το  έχουμε
έχουμε  περιττές δυνάμεις. Άρα
περιττές δυνάμεις. Άρα  .
.Αυτή τη λύση είχα !Demetres έγραψε:Για τοΚατερινόπουλος Νικόλας έγραψε:Άσκηση 1367
Να συγκρίνετε τους αριθμούς:
και
έχουμε
περιττές δυνάμεις. Οπότε
. Για το
έχουμε
περιττές δυνάμεις. Άρα
.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες