Έστω η απεικόνιση
 ,
, 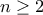 , ώστε για κάθε
, ώστε για κάθε  , ισχύει:
, ισχύει: Να εξετάσετε αν η
Να εξετάσετε αν η  είναι γραμμική απεικόνιση.
είναι γραμμική απεικόνιση.Συντονιστής: Demetres
 ,
, 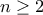 , ώστε για κάθε
, ώστε για κάθε  , ισχύει:
, ισχύει: Να εξετάσετε αν η
Να εξετάσετε αν η  είναι γραμμική απεικόνιση.
είναι γραμμική απεικόνιση.Ναι ισχύει και είναι πολύ απλό στην απόδειξή του.Σπύρος98 έγραψε: Έστω η απεικόνιση,
, ώστε για κάθε
, ισχύει:
Να εξετάσετε αν η
είναι γραμμική απεικόνιση.
 και
και 
 με τον ορισμό τους.
με τον ορισμό τους. , ως προς την κανονική βάση.
, ως προς την κανονική βάση.  είναι γραμμικός ισομορφισμός.
είναι γραμμικός ισομορφισμός. είναι γραμμική το ξέρω. Η διατύπωση όμως της άσκησης μου φάνηκε περίεργη.
είναι γραμμική το ξέρω. Η διατύπωση όμως της άσκησης μου φάνηκε περίεργη.
 είναι ισομορφισμός, αφού
είναι ισομορφισμός, αφού  (είναι σωστή η γραφή;).
(είναι σωστή η γραφή;).1) Προσοχή, στοΣπύρος98 έγραψε: 1) Ο πίνακας είναι ο
2) Ηείναι ισομορφισμός, αφού
(είναι σωστή η γραφή;).
 έχεις τυπογραφικές αβλεψίες. Το σωστό είναι
έχεις τυπογραφικές αβλεψίες. Το σωστό είναι 
 είναι
είναι  διότι εύκολα βλέπουμε ότι αν
διότι εύκολα βλέπουμε ότι αν 
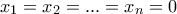 .
.  είναι επί (σχεδόν άμεσο). Και στα δύο χρησιμοποιώ ότι τα πεδία ορισμού και τιμών είναι ίδια.
είναι επί (σχεδόν άμεσο). Και στα δύο χρησιμοποιώ ότι τα πεδία ορισμού και τιμών είναι ίδια.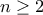 ";
";Μάριε η αρχική εκφώνηση το λέει.M.S.Vovos έγραψε:Κύριε Μιχάλη, μια ερώτηση.
Η εκφώνηση δεν θα έπρεπε να λέει "και για κάθε";
Μάριε,M.S.Vovos έγραψε:Εννοώ να χρησιμοποιήσει τον ποσοδείκτη.
 οποιοσδήποτε φυσικός ... "
οποιοσδήποτε φυσικός ... "  με
με  , ορίζουμε ... "
, ορίζουμε ... " Αφού είδαμε ότι είναι ισομορφισμός, βρες την αντίστροφη δηλώνοντας την εικόνα τουΣπύρος98 έγραψε: Έστω η απεικόνιση,
, ώστε για κάθε
, ισχύει:
Να εξετάσετε αν η
είναι γραμμική απεικόνιση.


Για ταMihalis_Lambrou έγραψε:Και μία ακόμη ερώτηση προς τον Σπύρο:
Αφού είδαμε ότι είναι ισομορφισμός, βρες την αντίστροφη δηλώνοντας την εικόνα τουΣπύρος98 έγραψε: Έστω η απεικόνιση,
, ώστε για κάθε
, ισχύει:
Να εξετάσετε αν η
είναι γραμμική απεικόνιση.

Κατόπιν βρες τον πίνακα του
 ,
,  με
με  και τον τύπο της γραμμικής απεικόνισης
και τον τύπο της γραμμικής απεικόνισης  προκύπτει ότι:
προκύπτει ότι:
 Επομένως ο αντίστροφος τελεστής θα είναι της μορφής
Επομένως ο αντίστροφος τελεστής θα είναι της μορφής  .
.Οι στάνταρ ερωτήσεις θα ήσαν: Για τουςΣπύρος98 έγραψε:Κάτι πιο δύσκολο σε αυτή την άσκηση τι θα μπορούσε να είναι;
 ,
,  ,
,  και
και 
 , καθώς και εκείνους που επιπλέον και ο
, καθώς και εκείνους που επιπλέον και ο  είναι αναλλοίωτος υπόχωρος,
είναι αναλλοίωτος υπόχωρος,  ,
, Κ. Λάμπρου ευχαριστώ για τα ερωτήματα. Όμως, δεν μπορώ να τα απαντήσω αφού η ύλη στην οποία αναφέρονται είναι Γραμμικής ΙΙ, που είναι στο 2ο εξάμηνο.Mihalis_Lambrou έγραψε:Οι στάνταρ ερωτήσεις θα ήσαν: Για τουςΣπύρος98 έγραψε:Κάτι πιο δύσκολο σε αυτή την άσκηση τι θα μπορούσε να είναι;,
,
και

α) Να βρείς τις ιδιοτιμές και τα ιδιοδιανύσματα μαζί με τις αλγεβρικές και γεωμετρικές τους πολλαπλότητες,
β) Να βρεις το χαρακτηριστικό και το ελάχιστο πολυώνυμο,
γ) Να βρεις τους αναλλοίωτους υπόχωρους, δηλαδή, καθώς και εκείνους που επιπλέον και ο
είναι αναλλοίωτος υπόχωρος,
δ) Να εξετάσεις αν διαγωνοποιείται και πώς,
ε) Να βρεις την κανονική μορφή Jordan,
στ) Να βρεις τους τελεστές με τους οποίους αντιμετατίθεται,
ζ) Να βρεις τους,
και πολλά άλλα.
Σε δεύτερη φάση θα δώσω και πιο δύσκολα ερωτήματα. Ας αρχίσεις από το στ).
Ωραία. Κάνε μόνο την στ) που είναι στις μέχρι τώρα γνώσεις σου. Για ευκολία κάνε την για την περίπτωσηΣπύρος98 έγραψε: Όμως, δεν μπορώ να τα απαντήσω αφού η ύλη στην οποία αναφέρονται είναι Γραμμικής ΙΙ, που είναι στο 2ο εξάμηνο.
 αλλά ας την εμπλουτίσω λίγο, οπότε την αναδιατυπώνω:
αλλά ας την εμπλουτίσω λίγο, οπότε την αναδιατυπώνω: παραπάνω (αλλά με
παραπάνω (αλλά με  ), να βρεθoύν όλοι οι
), να βρεθoύν όλοι οι  πίνακες
πίνακες  με
με 
 (δηλαδή τα πολυώνυμα του
(δηλαδή τα πολυώνυμα του  ), όπου
), όπου  ο ταυτοτικός, είναι πίνακες που ικανοποιούν την α).
ο ταυτοτικός, είναι πίνακες που ικανοποιούν την α). υπάρχουν άλλοι πίνακες που ικανοποιούν την α);
υπάρχουν άλλοι πίνακες που ικανοποιούν την α);  και τον
και τον  (εδώ
(εδώ  ο ανάστροφος, δηλαδή οι γραμμές του
ο ανάστροφος, δηλαδή οι γραμμές του  να γίνουν στήλες).
να γίνουν στήλες). που ικανοποιούν την α) για τον
που ικανοποιούν την α) για τον  είναι οι ίδιοι για τους ανίστοιχους που ικανοπούν την α) για τον
είναι οι ίδιοι για τους ανίστοιχους που ικανοπούν την α) για τον  ;
; ίσος με πολυώνυμο του
ίσος με πολυώνυμο του  ;
;Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης