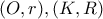 , με
, με  τέμνονται στα σημεία
τέμνονται στα σημεία  και εφάπτονται στα άκρα
και εφάπτονται στα άκρα σταθερού ευθύγραμμου τμήματος
 . Αν
. Αν  , να βρεθεί ο γεωμετρικός τόπος των σημείων
, να βρεθεί ο γεωμετρικός τόπος των σημείων 
Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
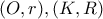 , με
, με  τέμνονται στα σημεία
τέμνονται στα σημεία  και εφάπτονται στα άκρα
και εφάπτονται στα άκρα  . Αν
. Αν  , να βρεθεί ο γεωμετρικός τόπος των σημείων
, να βρεθεί ο γεωμετρικός τόπος των σημείων 
Μπορούμε να δείξουμε ότιgeorge visvikis έγραψε:Locus.1.png
Δύο μεταβλητοί κύκλοι, με
τέμνονται στα σημεία
και εφάπτονται στα άκρα
σταθερού ευθύγραμμου τμήματος. Αν
, να βρεθεί ο γεωμετρικός τόπος των σημείων

 ισχύει
ισχύει 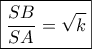 .
. κάθετες στις χορδές
κάθετες στις χορδές  τις τέμνουν στα
τις τέμνουν στα  ,
,  .Επειδή οι
.Επειδή οι  είναι μεσοκάθετες στις
είναι μεσοκάθετες στις 
 είναι το κέντρο του περιγεγραμμένου κύκλου του τριγώνου
είναι το κέντρο του περιγεγραμμένου κύκλου του τριγώνου  .
. ( Υπό χορδής κι εφαπτομένης) και
( Υπό χορδής κι εφαπτομένης) και 
 οπότε τα
οπότε τα 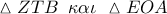 είναι όμοια, συνεπώς :
είναι όμοια, συνεπώς : . Με όμοιο τρόπο
. Με όμοιο τρόπο 
 αν πολλαπλασιάσουμε κατά μέλη τις
αν πολλαπλασιάσουμε κατά μέλη τις  θα έχουμε:
θα έχουμε: .
.  ανήκουν σε τμήμα του Απολλώνιου
ανήκουν σε τμήμα του Απολλώνιου  του οποίου
του οποίου 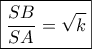 στο χρόνο τον οποίο οι κύκλοι
στο χρόνο τον οποίο οι κύκλοι  έχουν τουλάχιστο ένα κοινό σημείο .
έχουν τουλάχιστο ένα κοινό σημείο . ή στο τρίγωνο
ή στο τρίγωνο  για να έχω μια "καθαρά" γεωμετρική λύση.
για να έχω μια "καθαρά" γεωμετρική λύση.Ας δούμε άλλη μια γεωμετρική λύση διαφορετική από αυτή που έδωσε ο συνονόματος παραπάνω.george visvikis έγραψε:Locus.1.png
Δύο μεταβλητοί κύκλοι, με
τέμνονται στα σημεία
και εφάπτονται στα άκρα
σταθερού ευθύγραμμου τμήματος. Αν
, να βρεθεί ο γεωμετρικός τόπος των σημείων
 για διευκόλυνση των πράξεων και ονομάζω
για διευκόλυνση των πράξεων και ονομάζω  το σημείο τομής των ευθειών
το σημείο τομής των ευθειών  .
.  προκύπτει
προκύπτει  δηλαδή
δηλαδή  σταθερό.
σταθερό.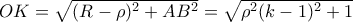 και
και 
 .
. έχουμε
έχουμε 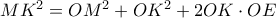

 .
. προκύπτει
προκύπτει 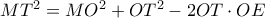
 γίνεται:
γίνεται: 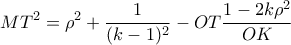
 γίνεται:
γίνεται:  σταθερό.
σταθερό. και ακτίνα
και ακτίνα  εκτός των σημείων που αυτός τέμνει την ευθεία
εκτός των σημείων που αυτός τέμνει την ευθεία  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες