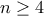 και για
και για  , η ανισότητα
, η ανισότητα 
[Δεν μοιάζει με τυπικό θέμα Πανελλαδικών. Τοποθετείται εδώ επειδή βγαίνει με Λογισμό, αν και προτιμητέα θα ήταν μια πιο στοιχειώδης απόδειξη. Η προέλευση και η εφαρμογή της ανισότητας θα αποκαλυφθούν αργότερα.]
Συντονιστής: Μπάμπης Στεργίου
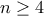 και για
και για  , η ανισότητα
, η ανισότητα 
Θέτουμε για ευκολία (αν και δεν είναι απαραίτητο)gbaloglou έγραψε:Να αποδειχθεί, για κάθε ακέραιοκαι για
, η ανισότητα
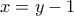 , οπότε
, οπότε  ή αλλιώς
ή αλλιώς  . Άρα
. Άρα 
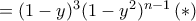
 .
. 
 , όπως θέλαμε.
, όπως θέλαμε. .
.  είναι
είναι ![= (1-y)^{3} (1-y^2)^{3} = \left [(1-y)(1-y^2)\right ]^{3} = (1-y)^{3} (1-y^2)^{3} = \left [(1-y)(1-y^2)\right ]^{3}](/forum/ext/geomar/texintegr/latexrender/pictures/6f22c78e38ba17ec45745de95dbc2553.png)

![(1-y)(1-y^2) \le \frac {3}{\sqrt [3] 4 } \approx 1,89 (1-y)(1-y^2) \le \frac {3}{\sqrt [3] 4 } \approx 1,89](/forum/ext/geomar/texintegr/latexrender/pictures/beb2e9d366dc017d1c516114eb252b74.png)
 και η τιμή του είναι
και η τιμή του είναι  )
)Εναλλακτική προσέγγιση (χωρίς παραγώγιση), γιαMihalis_Lambrou έγραψε:Ισοδύναμα θέλουμε
που ισχύει με περίσσευμα (παραγωγίζοντας ή αλλιώς βλέπουμε ότι το αριστερό μέλος έχει μέγιστο στοκαι η τιμή του είναι
)
 πάντοτε:
πάντοτε:![(1-y)(1-y^2)\leq \displaystyle\left[\frac{(1-y)+(1-y^2)}{2}\right]^2=\frac{(y^2+y-2)^2}{4}=\frac{\left[\left(y+\frac{1}{2}\right)^2-\frac{9}{4}\right]^2}{4}\leq (1-y)(1-y^2)\leq \displaystyle\left[\frac{(1-y)+(1-y^2)}{2}\right]^2=\frac{(y^2+y-2)^2}{4}=\frac{\left[\left(y+\frac{1}{2}\right)^2-\frac{9}{4}\right]^2}{4}\leq](/forum/ext/geomar/texintegr/latexrender/pictures/14f144a2d68c0524859504c47a7a2bcc.png)

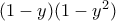 μεγιστοποιείται στο
μεγιστοποιείται στο ![[-1,1] [-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d060b17b29e0dae91a1cac23ea62281a.png) για
για  ;)]
;)]Γιώργο, μπορούμε.gbaloglou έγραψε:Μιχάλη μπορούμε όντως να συμπεράνουμε χωρίς παραγώγιση ότι ημεγιστοποιείται στο
για
;]
 στο
στο ![[-1,1] [-1,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d060b17b29e0dae91a1cac23ea62281a.png) . Ισοδύναμα
. Ισοδύναμα  , που δίνει το ζητούμενο και μάλιστα στο
, που δίνει το ζητούμενο και μάλιστα στο  .
. και για περιττό
και για περιττό  αντίστοιχα,
αντίστοιχα, 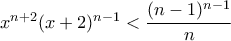 και
και  , όπου
, όπου  . Στην πρώτη περίπτωση αρκεί να αποδείξουμε, με δεδομένο τον μηδενισμό της
. Στην πρώτη περίπτωση αρκεί να αποδείξουμε, με δεδομένο τον μηδενισμό της  στα άκρα του
στα άκρα του ![[-2,0] [-2,0]](/forum/ext/geomar/texintegr/latexrender/pictures/5743178200081e6d6488c773516b1c6f.png) , ότι το μέγιστο της, σε σημείο μηδενισμού της παραγώγου, είναι μικρότερο του
, ότι το μέγιστο της, σε σημείο μηδενισμού της παραγώγου, είναι μικρότερο του  . Αναλόγως στην δεύτερη περίπτωση αρκεί να αποδείξουμε ότι το ελάχιστο της
. Αναλόγως στην δεύτερη περίπτωση αρκεί να αποδείξουμε ότι το ελάχιστο της  , σε σημείο μηδενισμού της παραγώγου, είναι μεγαλύτερο του
, σε σημείο μηδενισμού της παραγώγου, είναι μεγαλύτερο του  .
.![[x^{n+2}(x+2)^{n-1}]'=x^{n+1}(x+2)^{n-2}[(2n+1)x+2(n+2)] [x^{n+2}(x+2)^{n-1}]'=x^{n+1}(x+2)^{n-2}[(2n+1)x+2(n+2)]](/forum/ext/geomar/texintegr/latexrender/pictures/07f45c51e5f651c10a4c0610c00ae24d.png) προκύπτει ένα και μοναδικό σημείο μηδενισμού της παραγώγου, για
προκύπτει ένα και μοναδικό σημείο μηδενισμού της παραγώγου, για  . Παρατηρούμε επίσης ότι τα δύο ζητούμενα της προηγούμενης παραγράφου συμπτύσσονται σε ένα, συγκεκριμένα στην ανισότητα, για
. Παρατηρούμε επίσης ότι τα δύο ζητούμενα της προηγούμενης παραγράφου συμπτύσσονται σε ένα, συγκεκριμένα στην ανισότητα, για  ,
, 
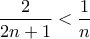 παρατηρούμε ότι αρκεί να ισχύει, για
παρατηρούμε ότι αρκεί να ισχύει, για  , η ανισότητα
, η ανισότητα
 (ισοδύναμη προς την
(ισοδύναμη προς την  ). Για
). Για  προκύπτει άμεσα από τις
προκύπτει άμεσα από τις  ,
,  για
για  , και
, και  για
για  .
.Και αν ... δεν γνωρίζουμε εκ των προτέρων ότι ηMihalis_Lambrou έγραψε:Γιώργο, μπορούμε.gbaloglou έγραψε:Μιχάλη μπορούμε όντως να συμπεράνουμε χωρίς παραγώγιση ότι ημεγιστοποιείται στο
για
;]
Θέλουμε να δείξουμεστο
. Ισοδύναμα
, που δίνει το ζητούμενο και μάλιστα στο
.
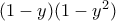 έχει τοπικό μέγιστο στο
έχει τοπικό μέγιστο στο  ... πάλι μπορούμε:
... πάλι μπορούμε: τέτοιο ώστε η
τέτοιο ώστε η  να διαιρείται δια του
να διαιρείται δια του  ... διαιρούμε δηλαδή το
... διαιρούμε δηλαδή το  δια του
δια του  παίρνοντας πηλίκο
παίρνοντας πηλίκο  και υπόλοιπο
και υπόλοιπο 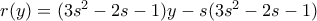 ... οπότε ο μηδενισμός του υπολοίπου* δίνει
... οπότε ο μηδενισμός του υπολοίπου* δίνει  (τοπικό ελάχιστο*) και
(τοπικό ελάχιστο*) και  (τοπικό μέγιστο*).
(τοπικό μέγιστο*). ισχύει η
ισχύει η  , και ισχύει επίσης η
, και ισχύει επίσης η  ή η
ή η  , τότε το
, τότε το  είναι τοπικό ελάχιστο ή τοπικό μέγιστο του πολυωνύμου, αντίστοιχα. (Στην περίπτωση μας
είναι τοπικό ελάχιστο ή τοπικό μέγιστο του πολυωνύμου, αντίστοιχα. (Στην περίπτωση μας  ,
,  ,
,  . Η απόδειξη του λήμματος είναι απλή αλλά απαιτεί εξοικείωση με την έννοια της συνέχειας ... που συνήθως διδάσκεται πριν από τα τοπικά ακρότατα, εδώ που τα λέμε
. Η απόδειξη του λήμματος είναι απλή αλλά απαιτεί εξοικείωση με την έννοια της συνέχειας ... που συνήθως διδάσκεται πριν από τα τοπικά ακρότατα, εδώ που τα λέμε Και με απλή εφαρμογή της ΑΜ-ΓΜ:gbaloglou έγραψε: Και αν ... δεν γνωρίζουμε εκ των προτέρων ότι ηέχει τοπικό μέγιστο στο
... πάλι μπορούμε:
![\displaystyle{(1-y)+(1-y)+2(1+y)\geq 3\sqrt[3]{2(1-y)^2(1+y)}\implies (1-y)(1-y^2)\leq \frac{32}{27}} \displaystyle{(1-y)+(1-y)+2(1+y)\geq 3\sqrt[3]{2(1-y)^2(1+y)}\implies (1-y)(1-y^2)\leq \frac{32}{27}}](/forum/ext/geomar/texintegr/latexrender/pictures/f0c034266323bcd28232db5e11d9d1fb.png)
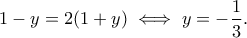
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες