 που ικανοποιούν τη σχέση
που ικανοποιούν τη σχέση 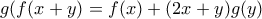 ,
,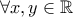 .
.Συντονιστές: achilleas, emouroukos, silouan
simantiris j. έγραψε:Να βρεθούν όλες οι συναρτήσειςπου ικανοποιούν τη σχέση
,
.
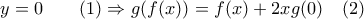

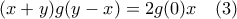

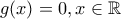 και
και 
 καθώς με την αντικατάσταση που κάνατε είναι
καθώς με την αντικατάσταση που κάνατε είναι 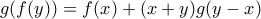 ,οπότε η (3) είναι λανθασμένη.
,οπότε η (3) είναι λανθασμένη.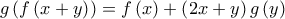

 και
και  στη σχέση
στη σχέση  βρίσκουμε ότι:
βρίσκουμε ότι: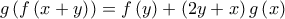
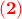
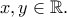
 και
και 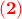 προκύπτει ότι
προκύπτει ότι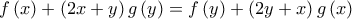
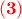
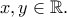
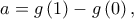
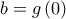 και
και 
 στη σχέση
στη σχέση 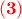 βρίσκουμε ότι:
βρίσκουμε ότι: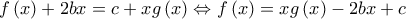
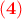

 και
και 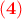 βρίσκουμε ότι:
βρίσκουμε ότι: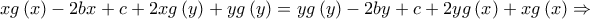
![\displaystyle{ \Rightarrow x\left[ {g\left( y \right) - b} \right] = y\left[ {g\left( x \right) - b} \right],} \displaystyle{ \Rightarrow x\left[ {g\left( y \right) - b} \right] = y\left[ {g\left( x \right) - b} \right],}](/forum/ext/geomar/texintegr/latexrender/pictures/5fb6b20a11ede8ec2b965ac943a6e96e.png)
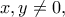 προκύπτει ότι
προκύπτει ότι
 Άρα, είναι
Άρα, είναι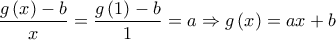
 Επειδή, όμως, η σχέση αυτή ισχύει και για
Επειδή, όμως, η σχέση αυτή ισχύει και για 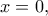 έχουμε ότι
έχουμε ότι  για κάθε
για κάθε 
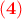 βρίσκουμε ότι
βρίσκουμε ότι 

 , βρίσκουμε ότι πρέπει να ισχύουν οι σχέσεις:
, βρίσκουμε ότι πρέπει να ισχύουν οι σχέσεις:
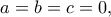 είτε
είτε 
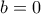 και
και 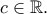

 για κάθε
για κάθε 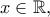

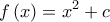 και
και 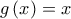 για κάθε
για κάθε 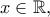 όπου
όπου  τυχαίος.
τυχαίος. μπορεί να αποδειχθεί πριν την εύρεση της μορφής των συναρτήσεων.
μπορεί να αποδειχθεί πριν την εύρεση της μορφής των συναρτήσεων.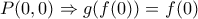
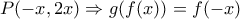
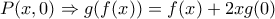 (1).
(1).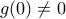 τότε από (1) η
τότε από (1) η  είναι 1-1.
είναι 1-1.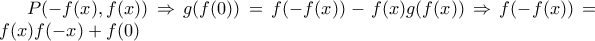
 το
το  έχουμε
έχουμε  λόγω του 1-1,άτοπο,άρα
λόγω του 1-1,άτοπο,άρα  .Η συνέχεια όπως πάνω.
.Η συνέχεια όπως πάνω.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες