 παραγωγίσιμη στο
παραγωγίσιμη στο 
με
 και
και 
Δείξτε ότι
1)Υπάρχει
 με
με 
2)Για
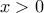 έχουμε
έχουμε 
3)Η
 παίρνει μέγιστη τιμή σε κάποιο
παίρνει μέγιστη τιμή σε κάποιο 
4)
 και
και 
5)Βρείτε το
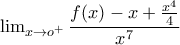
Συντονιστής: emouroukos
 παραγωγίσιμη στο
παραγωγίσιμη στο 
 και
και 
 με
με 
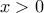 έχουμε
έχουμε 
 παίρνει μέγιστη τιμή σε κάποιο
παίρνει μέγιστη τιμή σε κάποιο 
 και
και 
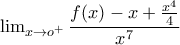
Σταύρο, την έχω λύσει καιρό τώρα αλλά δεν έγραφα την λύση γιατί οι πράξεις, τουλάχιστον όπως το είδα, είναι πάρα πολλές.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Εστωπαραγωγίσιμη στο
μεκαι
Δείξτε ότι
1)Υπάρχειμε
2)Γιαέχουμε
3)Ηπαίρνει μέγιστη τιμή σε κάποιο
4)και
5)Βρείτε το
 και
και  , αντίστοιχα. Για το 5) η απάντηση είναι
, αντίστοιχα. Για το 5) η απάντηση είναι 
 οπότε ολοκληρώνοντας έχουμε
οπότε ολοκληρώνοντας έχουμε 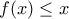 . Πίσω στην αρχική,
. Πίσω στην αρχική,  . Oλοκληρώνοντας έχουμε
. Oλοκληρώνοντας έχουμε  .
. 

 , μετά το
, μετά το 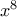 , δεν χρειάζεται να τις καταγράψω. Θα αρκούσε ένα
, δεν χρειάζεται να τις καταγράψω. Θα αρκούσε ένα  αλλά επειδή οι μαθητές που μας διαβάζουν μπορεί να μην ξέρουν την έννοια, κάνω το κόπο των πράξεων μέχρις εσχάτων. Αυτό που έχει σημασία είναι ότι τα δύο μέρη εκατέρωθεν της
αλλά επειδή οι μαθητές που μας διαβάζουν μπορεί να μην ξέρουν την έννοια, κάνω το κόπο των πράξεων μέχρις εσχάτων. Αυτό που έχει σημασία είναι ότι τα δύο μέρη εκατέρωθεν της  είναι ολόϊδια μέχρι το
είναι ολόϊδια μέχρι το  ).
).  και διαιρώντας με το
και διαιρώντας με το  καταλήγουμε
καταλήγουμε 
 , καταλήγουμε ότι
, καταλήγουμε ότι 
 έχει παραγώγους όλων τάξεων που μάλιστα είναι φραγμένες π.χ στο
έχει παραγώγους όλων τάξεων που μάλιστα είναι φραγμένες π.χ στο ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png)

 μπορούμε να την έχουμε σε ανάπτυγμα δυνάμεων του
μπορούμε να την έχουμε σε ανάπτυγμα δυνάμεων του  κοντά στο
κοντά στο 
 θα είναι
θα είναι 





 παίρνουμε
παίρνουμε 


 για
για  κοντά στο
κοντά στο  όσο καλά θέλουμε.
όσο καλά θέλουμε. οπότε θα είχαμε
οπότε θα είχαμε  και
και 
 και θα βρίσκαμε το ανάπτυγμα της
και θα βρίσκαμε το ανάπτυγμα της 
Ξεχάστηκε.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Εστωπαραγωγίσιμη στο
μεκαι
Δείξτε ότι
1)Υπάρχειμε
2)Γιαέχουμε
3)Ηπαίρνει μέγιστη τιμή σε κάποιο
4)και
5)Βρείτε το
 για κάθε
για κάθε  . Τότε
. Τότε  αύξουσα και άρα
αύξουσα και άρα  αφού
αφού  ,και μάλιστα (αφού
,και μάλιστα (αφού 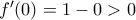 ) υπάρχει
) υπάρχει  με
με  . Οπότε για
. Οπότε για 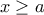 έχουμε
έχουμε  και άρα
και άρα  .
. καθώς
καθώς  .
.  και από το 1) υπάρχει
και από το 1) υπάρχει  με
με  . Όμως η
. Όμως η  είναι συνεχής ως ίση με την συνεχή
είναι συνεχής ως ίση με την συνεχή  , οπότε υπάρχει
, οπότε υπάρχει  με
με  και άρα
και άρα  .
.
 έχουμε μέγιστο. Ειδικά δείξαμε ότι σε κάθε σημείο ακροτάτου έχουμε μέγιστο.
έχουμε μέγιστο. Ειδικά δείξαμε ότι σε κάθε σημείο ακροτάτου έχουμε μέγιστο. . Άρα από το μέγιστο και πέρα είναι
. Άρα από το μέγιστο και πέρα είναι  , οπότε
, οπότε  και ειδικά δεν μηδενίζεται πουθενά (και άρα γνήσια θετική). Επίσης η
και ειδικά δεν μηδενίζεται πουθενά (και άρα γνήσια θετική). Επίσης η  είναι γνήσια αύξουσα μέχρι το μέγιστο (αλλιώς η παράγωγος θα μηδενιζόταν κάπου στο ενδιάμεσο) και εύκολα ολοκληρώνουμε το 2.
είναι γνήσια αύξουσα μέχρι το μέγιστο (αλλιώς η παράγωγος θα μηδενιζόταν κάπου στο ενδιάμεσο) και εύκολα ολοκληρώνουμε το 2.  με
με  τότε μπορούμε να θεωρήσουμε ότι το
τότε μπορούμε να θεωρήσουμε ότι το  είναι το infimum του κλειστού συνόλου
είναι το infimum του κλειστού συνόλου  . Ειδικά
. Ειδικά  λόγω συνέχειας. Επίσης
λόγω συνέχειας. Επίσης 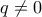 διότι
διότι  . Όμως τότε
. Όμως τότε  , που σημαίνει ότι η
, που σημαίνει ότι η  είναι γνήσια αύξουσα σε περιοχή του
είναι γνήσια αύξουσα σε περιοχή του  που αντιφάσκει στον ορισμό του
που αντιφάσκει στον ορισμό του  ως infimum (αριστερά του υπάρχουν σημεία με
ως infimum (αριστερά του υπάρχουν σημεία με  . Και λοιπά.
. Και λοιπά. . Άρα το όριο
. Άρα το όριο  υπάρχει. Αν
υπάρχει. Αν 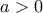 τότε
τότε  για όλα τα μεγάλα
για όλα τα μεγάλα  , άρα σε τέτοια
, άρα σε τέτοια  είναι
είναι  , και άρα
, και άρα  , άτοπο.
, άτοπο.  και ολοκληρώνεται η απόδειξη του
και ολοκληρώνεται η απόδειξη του  .
. .
. αρκεί το
αρκεί το  να υπάρχει.
να υπάρχει. είναι αύξουσα από κάπου και πέρα.
είναι αύξουσα από κάπου και πέρα. (*)
(*) για
για  Τελειώσαμε.
Τελειώσαμε. για
για  Τότε η
Τότε η  θα είναι κοίλη και επειδή
θα είναι κοίλη και επειδή  για μεγάλα
για μεγάλα 
 που είναι ΑΤΟΠΟ
που είναι ΑΤΟΠΟ με
με  και
και




 )
)Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 0 επισκέπτες