Έστω τα αντιρρόπως όμοια τρίγωνα (*)
 με ομόλογες κορυφές τα ζεύγη
με ομόλογες κορυφές τα ζεύγη  και λόγο ομοιότητας
και λόγο ομοιότητας  του
του  προς το
προς το  . Να δειχθεί
. Να δειχθεί  είναι συνευθειακά, όπου
είναι συνευθειακά, όπου  σημεία των ευθειών
σημεία των ευθειών  για τα οποία ισχύει:
για τα οποία ισχύει: 
(*)
Στάθης
Συντονιστής: ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ
 με ομόλογες κορυφές τα ζεύγη
με ομόλογες κορυφές τα ζεύγη  και λόγο ομοιότητας
και λόγο ομοιότητας  του
του  προς το
προς το  . Να δειχθεί
. Να δειχθεί  είναι συνευθειακά, όπου
είναι συνευθειακά, όπου  σημεία των ευθειών
σημεία των ευθειών  για τα οποία ισχύει:
για τα οποία ισχύει: 
 οι πλευρές τους δεν τέμνονται και
οι πλευρές τους δεν τέμνονται και  κυρτό τετράπλευρο και σημεία
κυρτό τετράπλευρο και σημεία  των
των  αντίστοιχα
αντίστοιχα
 είναι παράλληλη με την διχοτόμο της γωνίας που σχηματίζουν οι προεκτάσεις των
είναι παράλληλη με την διχοτόμο της γωνίας που σχηματίζουν οι προεκτάσεις των 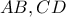
 κυρτό τετράπλευρο ώστε
κυρτό τετράπλευρο ώστε  .
. είναι παράλληλες.
είναι παράλληλες. και
και 
 έχουμε
έχουμε  .
.
 παίρνουμε ότι
παίρνουμε ότι 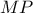 είναι παράλληλη στην διχοτόμο της
είναι παράλληλη στην διχοτόμο της 
 παίρνουμε ότι η
παίρνουμε ότι η  είναι παράλληλη στην διχοτόμο της
είναι παράλληλη στην διχοτόμο της  .
. είναι παράλληλες τα
είναι παράλληλες τα  είναι σε ευθεία.
είναι σε ευθεία. , είναι τα δοσμένα αντιρρόπως όμοια τρίγωνα, με λόγο ομοιότητας
, είναι τα δοσμένα αντιρρόπως όμοια τρίγωνα, με λόγο ομοιότητας  και
και  , είναι τα σημεία επί των
, είναι τα σημεία επί των  αντιστοίχως, ώστε να ισχύει
αντιστοίχως, ώστε να ισχύει  .
.
 Έστω
Έστω  , τα σημεία ώστε τα τετράπλευρα
, τα σημεία ώστε τα τετράπλευρα  να είναι παραλληλόγραμμα.
να είναι παραλληλόγραμμα. και
και  και
και  , σύμφωνα με το Θεώρημα Θαλή , προκύπτει ότι τα σημεία
, σύμφωνα με το Θεώρημα Θαλή , προκύπτει ότι τα σημεία  είναι συνευθειακά και ισχύει
είναι συνευθειακά και ισχύει 
 και
και  , προκύπτει ότι στο τρίγωνο
, προκύπτει ότι στο τρίγωνο  , η ευθεία
, η ευθεία 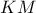 ταυτίζεται με την διχοτόμο της γωνίας
ταυτίζεται με την διχοτόμο της γωνίας  .
. Έστω
Έστω  , τα σημεία ώστε τα τετράπλευρα
, τα σημεία ώστε τα τετράπλευρα  να είναι παραλληλόγραμμα.
να είναι παραλληλόγραμμα. είναι συνευθειακά και ότι στο τρίγωνο
είναι συνευθειακά και ότι στο τρίγωνο  , η ευθεία
, η ευθεία  ταυτίζεται με την διχοτόμο της γωνίας
ταυτίζεται με την διχοτόμο της γωνίας  .
. τώρα, ταυτίζονται λόγω
τώρα, ταυτίζονται λόγω  και το ζητούμενο έχει αποδεχθεί.
και το ζητούμενο έχει αποδεχθεί..ΣΤΑΘΗΣ ΚΟΥΤΡΑΣ έγραψε:αντιρρόπως όμοια τρίγωνα.pngΜε αφορμή τα αντιρρόπως ίσα τρίγωνα
Έστω τα αντιρρόπως όμοια τρίγωνα (*)με ομόλογες κορυφές τα ζεύγη
και λόγο ομοιότητας
του
προς το
. Να δειχθεί
είναι συνευθειακά, όπου
σημεία των ευθειών
για τα οποία ισχύει:

(*)
Ας δούμε και μια διαφορετική προσέγγιση. Έστωοι τομές των
με τις εκ των
παράλληλες προς τις
αντίστοιχα. Τότε είναι

και με ομοίως προκύπτει
.
[attachment=0]Αντιρρόπως όμοια τρίγωνα.png[/attachment]
Επειδή προφανώςαπό
σύμφωνα με την
απλή συνευθειακότητα προκύπτει ότισυνευθειακά άρα από
συνευθειακά και το ζητούμενο έχει αποδειχθεί.
Στάθης
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες