Και οι δύο αποδείξεις είναι προβληματικές.
dopfev έγραψε:

άρα και η αντίστροφη γνησίως αύξουσα.
Στο τρίτο

δεν αποδείχθηκε το βήμα. Ίσα-ίσα είναι ισοδύναμο με το αποδεικτέο γιατί για να πάμε από μία ανισότητα της μορφής

στην

(εδώ

) , είναι σαν να θεωρούμε ότι η

είναι γνήσια αύξουσα οπότε ισχύει

Δηλαδή η απόδειξη έχει ουσιαστικό κενό γιατί χρησιμοποιεί το αποδεικτέο.
Για την δεύτερη απόδειξη
dopfev έγραψε: 
.
το κενό είναι πιο σοβαρό: Η απόδειξη της μονοτονίας μιάς

απαιτεί
να υποθέσουμε 
και από αυτό τα δείξουμε

.
Η εν λόγω απόδειξη, όπου η

είναι η

, ούτε καν ξεκινά από την υπόθεση

. Οπότε η απόδειξη δεν λέει απολύτως τίποτα. Δεν είναι σωστή ούτε σε σύλληψη.
Για χάρη της πληρότητας, ας βάλω μία απόδειξη της ζητούμενης ιδιότητας παρόλο που είναι πολλή γνωστή:
Έστω

. Θέλουμε να δείξουμε ότι ισχύει

. Αν δεν ίσχυε αυτό τότε από την αρχή της τριχοτομίας της διάταξης θα ίσχυε

. Αλλά τότε, από το γεγονός ότι η

είναι γνήσια αύξουσα, θα είχαμε

, δηλαδή

. Αλλά αυτό αντιβαίνει στην υπόθεση

, και λοιπά.
 έχει το ίδιο είδος μονοτονίας με την
έχει το ίδιο είδος μονοτονίας με την  , οπότε αν
, οπότε αν  γνησίως αύξουσα τότε για
γνησίως αύξουσα τότε για  :
: άρα και η αντίστροφη γνησίως αύξουσα.
άρα και η αντίστροφη γνησίως αύξουσα. . Είναι λάθος η σκέψη του ή στέκει; Μπορώ από τις τυχαίες τιμές της συνάρτησης να καταλήξω στην ανισότητα των σημείων και να ισχυριστώ ότι η συνάρτηση είναι γνησίως αύξουσα ή φθίνουσα; Ευχαριστώ...
. Είναι λάθος η σκέψη του ή στέκει; Μπορώ από τις τυχαίες τιμές της συνάρτησης να καταλήξω στην ανισότητα των σημείων και να ισχυριστώ ότι η συνάρτηση είναι γνησίως αύξουσα ή φθίνουσα; Ευχαριστώ...
 δεν αποδείχθηκε το βήμα. Ίσα-ίσα είναι ισοδύναμο με το αποδεικτέο γιατί για να πάμε από μία ανισότητα της μορφής
δεν αποδείχθηκε το βήμα. Ίσα-ίσα είναι ισοδύναμο με το αποδεικτέο γιατί για να πάμε από μία ανισότητα της μορφής  στην
στην  (εδώ
(εδώ  ) , είναι σαν να θεωρούμε ότι η
) , είναι σαν να θεωρούμε ότι η 
 απαιτεί
απαιτεί  και από αυτό τα δείξουμε
και από αυτό τα δείξουμε  .
. . Θέλουμε να δείξουμε ότι ισχύει
. Θέλουμε να δείξουμε ότι ισχύει  . Αν δεν ίσχυε αυτό τότε από την αρχή της τριχοτομίας της διάταξης θα ίσχυε
. Αν δεν ίσχυε αυτό τότε από την αρχή της τριχοτομίας της διάταξης θα ίσχυε  . Αλλά τότε, από το γεγονός ότι η
. Αλλά τότε, από το γεγονός ότι η  , δηλαδή
, δηλαδή  . Αλλά αυτό αντιβαίνει στην υπόθεση
. Αλλά αυτό αντιβαίνει στην υπόθεση  τότε
τότε  το οποίο σημαίνει ότι η
το οποίο σημαίνει ότι η  . Ο μαθητής έχει μόνο
. Ο μαθητής έχει μόνο  . Από που βγάζουμε το συμπέρασμα ότι έχει αντιθετοαντιστροφή στον νου του;
. Από που βγάζουμε το συμπέρασμα ότι έχει αντιθετοαντιστροφή στον νου του; χρησιμοποιώ και την μονοτονία της
χρησιμοποιώ και την μονοτονία της  , άσχετα αν τα
, άσχετα αν τα  είναι τιμές της αντίστροφης...
είναι τιμές της αντίστροφης... και να καταλήξω σε
και να καταλήξω σε  ή
ή  ; Ένα παράδειγμα:
; Ένα παράδειγμα: . Να μελετήσετε την μονοτονία της.
. Να μελετήσετε την μονοτονία της.  .Για
.Για  . Είναι τελείως λάθος αυτή η αντιμετώπιση; Ευχαριστώ πολύ!
. Είναι τελείως λάθος αυτή η αντιμετώπιση; Ευχαριστώ πολύ! Να δείξετε πως η
Να δείξετε πως η  . Είναι
. Είναι 
 καθώς και τη σχέση διάταξης ανάμεσα τους. Έπειτα, εκμεταλλευόμενοι τη δοθείσα δείχνουμε πως ισχύει
καθώς και τη σχέση διάταξης ανάμεσα τους. Έπειτα, εκμεταλλευόμενοι τη δοθείσα δείχνουμε πως ισχύει  όπου
όπου  .
. έχουν το ίδιο είδος μονοτονίας προκειμένου να δείξουμε πως
έχουν το ίδιο είδος μονοτονίας προκειμένου να δείξουμε πως 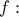 γν. αύξουσα. Το συγκεκριμένο θεώρημα όμως πουθενά δεν αναφέρεται στο βιβλίο.
γν. αύξουσα. Το συγκεκριμένο θεώρημα όμως πουθενά δεν αναφέρεται στο βιβλίο. και
και  δεν είναι πρόβλημα.
δεν είναι πρόβλημα. έχει πρόβλημα ή όχι; Χρησιμοποιώ δηλαδή χωρίς να το καταλαβαίνω και την μονοτονία της
έχει πρόβλημα ή όχι; Χρησιμοποιώ δηλαδή χωρίς να το καταλαβαίνω και την μονοτονία της  την οποία δεν απέδειξες. Ένας τρόπος να το δείξεις είναι με αντιθετοαντιστροφή. Άλλος τρόπος είναι να χρησιμοποιήσεις ως γνωστή την μονοτονία της
την οποία δεν απέδειξες. Ένας τρόπος να το δείξεις είναι με αντιθετοαντιστροφή. Άλλος τρόπος είναι να χρησιμοποιήσεις ως γνωστή την μονοτονία της  . Βλέπε π.χ. Νεγρεπόντης κλπ, Απειροστικός Λογισμός, τ. 1., σ. 132.
. Βλέπε π.χ. Νεγρεπόντης κλπ, Απειροστικός Λογισμός, τ. 1., σ. 132. , τότε από την απόδειξή σου λείπουν όλα τα "
, τότε από την απόδειξή σου λείπουν όλα τα " "
" με σύνολο τιμών το
με σύνολο τιμών το  :
:
 , το οποίο
, το οποίο