 τέμνονται στα
τέμνονται στα  και έστω
και έστω  το κοινό εξωτερικό εφαπτόμενο τμήμα τους που βρίσκεται πιο κοντά στο
το κοινό εξωτερικό εφαπτόμενο τμήμα τους που βρίσκεται πιο κοντά στο  . Αν η κάθετη από το
. Αν η κάθετη από το  στη
στη 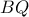 τέμνει την
τέμνει την  στο
στο  , να δείξετε ότι
, να δείξετε ότι 
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
Μη αναγνωσμένη δημοσίευση από george visvikis » Τρί Σεπ 27, 2016 11:58 pm
 τέμνονται στα
τέμνονται στα  και έστω
και έστω  το κοινό εξωτερικό εφαπτόμενο τμήμα τους που βρίσκεται πιο κοντά στο
το κοινό εξωτερικό εφαπτόμενο τμήμα τους που βρίσκεται πιο κοντά στο  . Αν η κάθετη από το
. Αν η κάθετη από το  στη
στη 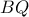 τέμνει την
τέμνει την  στο
στο  , να δείξετε ότι
, να δείξετε ότι 
Μη αναγνωσμένη δημοσίευση από dement » Τετ Σεπ 28, 2016 2:58 pm
 . Τότε
. Τότε  και λόγω των ομοίων τριγώνων
και λόγω των ομοίων τριγώνων 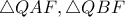 ισχύει
ισχύει  .
. (γιατί
(γιατί 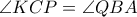 και
και 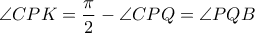 και δουλεύουμε με νόμο ημιτόνων στο
και δουλεύουμε με νόμο ημιτόνων στο  ) οπότε παίρνουμε
) οπότε παίρνουμε 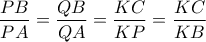 .
. και την
και την  προκύπτει
προκύπτει 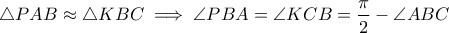 που ολοκληρώνει την απόδειξη.
που ολοκληρώνει την απόδειξη.Επιστροφή σε “Γεωμετρία (Juniors) - Παλαιότερες Συζητήσεις”
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες
Powered by phpBB® Forum Software © phpBB Limited
Style από Arty - Ενημέρωση phpBB 3.2 από MrGaby
Ελληνική μετάφραση από το phpbbgr.com
Το www.mathematica.gr δημιουργήθηκε από τους Γρηγόρη Κωστάκο και Αλέξανδρο Συγκελάκη
με τη βοήθεια των Στέλιου Μόσχογλου και Γιώργου Μαργαρίτη
GZIP: Off