Δημοσιεύω επιτέλους (μετά από αρκετά προβληματάκια στη μορφοποίηση LaTeX...) τη λύση μου:
α) Η σχέση της εκφώνησης μπορεί να γραφτεί ως:

.
Ορίζουμε τις εξής συναρτήσεις:

![h(x) = \begin{cases} g(\tan x), -\frac{\pi}{2}<x<\frac{\pi}{2} \\[2ex] 0, x= \{ -\frac{\pi}{2}, \frac{\pi}{2} \} \end{cases} h(x) = \begin{cases} g(\tan x), -\frac{\pi}{2}<x<\frac{\pi}{2} \\[2ex] 0, x= \{ -\frac{\pi}{2}, \frac{\pi}{2} \} \end{cases}](/forum/ext/geomar/texintegr/latexrender/pictures/f33a38035277ece5767168e19c7ea0de.png)
Η

είναι παραγωγίσιμη και συνεχής στο

ως διαφορά παραγωγίσιμων στο

συναρτήσεων, με παράγωγο:

Από την (1) τώρα προκύπτει ότι:

.
Η

είναι συνεχής στο
![[-\frac{\pi}{2}, \frac{\pi}{2}] [-\frac{\pi}{2}, \frac{\pi}{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/c48aa04a4a57f98397ce175c220a0c6f.png)
ως σύνθεση συνεχών συναρτήσεων και επειδή:

και

(δεν έχω γράψει αναλυτικά τα όρια της

αλλά βγαίνουν πολύ εύκολα σε συνδυασμό με τα δεδομένα της εκφώνησης για τα όρια της

). Ταυτόχρονα, η

είναι παραγωγίσιμη στο

(δεν μας ενδιαφέρει τι γίνεται στο κλειστό διάστημα) ως σύνθεση παραγωγίσιμων συναρτήσεων σε κατάλληλα διαστήματα, με παράγωγο:

.
Θα δείξουμε ότι
![h(x)=0,\forall x\in [-\frac{\pi}{2}, \frac{\pi}{2}] h(x)=0,\forall x\in [-\frac{\pi}{2}, \frac{\pi}{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/6dd4cd2730d5217de7258b46eb4d14d1.png)
.
Έστω ότι υπάρχει κάποιο

τέτοιο ώστε

. Διακρίνουμε περιπτώσεις:
Αν

, τότε:
- Η

δεν παρουσιάζει μέγιστο στα άκρα του διαστήματος (επειδή αν υποθέσουμε ότι παρουσίαζε εκεί, τότε

, άτοπο διότι

) οπότε από το Θεώρημα Μέγιστης και Ελάχιστης Τιμής προκύπτει ότι υπάρχει κάποιο

τέτοιο ώστε
![h(x)\leq h(x_{max}), \forall x\in [-\frac{\pi}{2}, \frac{\pi}{2}] (4) h(x)\leq h(x_{max}), \forall x\in [-\frac{\pi}{2}, \frac{\pi}{2}] (4)](/forum/ext/geomar/texintegr/latexrender/pictures/a834407d78dbeb521fbe34938adc0556.png)
. Σε αυτή τη σχέση αντικαθιστούμε

οπότε

άρα

.
- Από την εφαρμογή του Θεωρήματος Fermat, εξαιτίας της σχέσης (4) και εφόσον

, προκύπτει ότι:

άρα λαμβάνοντας υπόψη τη σχέση (3) έχουμε:

συνεπώς αντικαθιστούμε στη σχέση (2)

οπότε:

, άτοπο εξαιτίας της σχέσης (5).
Αν

, τότε όμοια έχουμε:
- Η

δεν παρουσιάζει ελάχιστο στα άκρα του διαστήματος (επειδή αν υποθέσουμε ότι παρουσίαζε εκεί, τότε

, άτοπο διότι

) οπότε από το Θεώρημα Μέγιστης και Ελάχιστης Τιμής προκύπτει ότι υπάρχει κάποιο

τέτοιο ώστε
![h(x)\geq h(x_{min}), \forall x\in [-\frac{\pi}{2}, \frac{\pi}{2}] (6) h(x)\geq h(x_{min}), \forall x\in [-\frac{\pi}{2}, \frac{\pi}{2}] (6)](/forum/ext/geomar/texintegr/latexrender/pictures/aa7ab970c7aacc2797523ee2bc5d60b5.png)
. Σε αυτή τη σχέση αντικαθιστούμε

οπότε

άρα

.
- Από την εφαρμογή του Θεωρήματος Fermat, εξαιτίας της σχέσης (6) και εφόσον

, προκύπτει ότι:

άρα λαμβάνοντας υπόψη τη σχέση (3) έχουμε:

συνεπώς αντικαθιστούμε στη σχέση (2)

οπότε:

, άτοπο εξαιτίας της σχέσης (7).
Καταλήξαμε σε άτοπο γιατί υποθέσαμε ότι υπάρχει κάποιο

τέτοιο ώστε

. Άρα, εφόσον

, ισχύει ότι:
![h(x)=0,\forall x\in [-\frac{\pi}{2}, \frac{\pi}{2}] h(x)=0,\forall x\in [-\frac{\pi}{2}, \frac{\pi}{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/6dd4cd2730d5217de7258b46eb4d14d1.png)
συνεπώς

.
Πάμε τώρα να αποδείξουμε ότι η σχέση (8) συνεπάγεται ότι

.
Έστω

. Η

είναι συνεχής και γνησίως αύξουσα στο

με σύνολο τιμών (προσδιορισμός με όρια στα άκρα του ανοικτού διαστήματος) το

. Επομένως, είναι και αντιστρέψιμη με αντίστροφο

με

.
Δηλαδή τελικά, θέτοντας στην (8) όπου

το

για κάθε

ισχύει:

και το ζητούμενο απεδείχθη.
β) Από γνωστή εφαρμογή του σχολικού βιβλίου ισχύει:

με την ισότητα μόνο για

οπότε θέτοντας σε αυτή όπου

το

για κάθε

έχουμε:

με την ισότητα μόνο για

.
Έτσι, είναι:

οπότε θέτοντας όπου

το

για κάθε

προκύπτει ότι:

με την ισότητα μόνο για

.
Οπότε, τελικά, για κάθε

ισχύει ότι:

δηλαδή

.
γ) Το πρώτο μέρος της διπλής ανισότητας που θέλουμε να αποδείξουμε βγαίνει εύκολα: Επειδή

θέτοντας όπου

το

για κάθε

προκύπτει ότι:

δηλαδή

, άρα, σύμφωνα με γνωστό πόρισμα του σχολικού βιβλίου,

οπότε πάλι σύμφωνα με θεώρημα του σχολικού βιβλίου (στα όρια)

επειδή το όριο υπάρχει σύμφωνα με την εκφώνηση.
Το δεύτερο μέρος απαιτεί την ελαφρά κατεργασία της ανισότητας του (β) ως εξής: για κάθε

ισχύει ότι:

άρα (επειδή και τα δύο μέλη είναι θετικά)

οπότε από το (β) προκύπτει ότι:

άρα σύμφωνα με γνωστό πόρισμα του σχολικού βιβλίου έχουμε:
![\int\limits_{1}^{\lambda}{\left( \frac{1}{x^2}-f(x)\right) \, dx} > 0 \Rightarrow \int\limits_{1}^{\lambda}f(x)\, dx < \int\limits_{1}^{\lambda}\frac{1}{x^2}\, dx = \left[ -\frac{1}{x}\right]_{1}^{\lambda} = 1 - \frac{1}{\lambda} \int\limits_{1}^{\lambda}{\left( \frac{1}{x^2}-f(x)\right) \, dx} > 0 \Rightarrow \int\limits_{1}^{\lambda}f(x)\, dx < \int\limits_{1}^{\lambda}\frac{1}{x^2}\, dx = \left[ -\frac{1}{x}\right]_{1}^{\lambda} = 1 - \frac{1}{\lambda}](/forum/ext/geomar/texintegr/latexrender/pictures/e891de91244b8118b54b7dd1306ecedb.png)
οπότε πάλι σύμφωνα με θεώρημα του σχολικού βιβλίου (στα όρια) είναι:

.
Άρα, τελικά, αποδείξαμε ότι

.
Το άλλο, λιγάκι πιο περιορισμένο διάστημα,

, μπορούμε να το λάβουμε
εκτός σχολικής ύλης με απευθείας ολοκλήρωση της σχέσης του (β) και τριγωνομετρική αντικατάσταση

στο ολοκλήρωμα που προκύπτει.
Συγγνώμη που είναι τόσο χονδροειδής η ανισότητα στο (β) και στο (γ).
 τέτοια ώστε
τέτοια ώστε  και για κάθε
και για κάθε  να ισχύει:
να ισχύει: 
 για κάθε
για κάθε 
 για κάθε
για κάθε 
 , για
, για  . Αν γνωρίζουμε ότι υπάρχει το
. Αν γνωρίζουμε ότι υπάρχει το  , να αποδείξετε ότι
, να αποδείξετε ότι  .
.
 .Η σχέση γράφεται
.Η σχέση γράφεται  .
. ,οπότε
,οπότε  .
. είναι συνεχής,θα έχει ακρότατο (διαισθητικά μπορούμε να το καταλάβουμε αυτό,αλλά υπάρχει και απόδειξη εντός ύλης).
είναι συνεχής,θα έχει ακρότατο (διαισθητικά μπορούμε να το καταλάβουμε αυτό,αλλά υπάρχει και απόδειξη εντός ύλης). στη θέση
στη θέση  .Από Fermat προκύπτει
.Από Fermat προκύπτει  .
. όπου
όπου  το
το  .Επομένως
.Επομένως  .
. ,άρα η
,άρα η  .Έστω πως υπάρχει
.Έστω πως υπάρχει  με
με  .
. ισχύει
ισχύει  ,οπότε
,οπότε  ,άτοπο και τελειώσαμε.
,άτοπο και τελειώσαμε.
 για
για 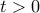 . Έτσι
. Έτσι  για
για 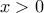 (όχι μόνο
(όχι μόνο  που ζητά η άσκηση) και άρα
που ζητά η άσκηση) και άρα 
 . Στο όριο
. Στο όριο  που είναι βέβαια αρκετά μικρότερο από το
που είναι βέβαια αρκετά μικρότερο από το  (και μάλιστα μικρότερο από το
(και μάλιστα μικρότερο από το  που
που 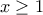 για να δείξει λιγάκι και προς το (γ) επειδή εγώ σκέφτηκα κάτι λίγο διαφορετικό. Κάθε άλλη λύση όμως (και μάλιστα ισχυρότερη) είναι αποδεκτή!!
για να δείξει λιγάκι και προς το (γ) επειδή εγώ σκέφτηκα κάτι λίγο διαφορετικό. Κάθε άλλη λύση όμως (και μάλιστα ισχυρότερη) είναι αποδεκτή!! 


 ενώ μπορούμε ΑΠΛΟΥΣΤΕΡΑ και ΚΑΛΥΤΕΡΑ να χρησιμοποιήσουμε την
ενώ μπορούμε ΑΠΛΟΥΣΤΕΡΑ και ΚΑΛΥΤΕΡΑ να χρησιμοποιήσουμε την  .
.  .
.
![h(x) = \begin{cases} g(\tan x), -\frac{\pi}{2}<x<\frac{\pi}{2} \\[2ex] 0, x= \{ -\frac{\pi}{2}, \frac{\pi}{2} \} \end{cases} h(x) = \begin{cases} g(\tan x), -\frac{\pi}{2}<x<\frac{\pi}{2} \\[2ex] 0, x= \{ -\frac{\pi}{2}, \frac{\pi}{2} \} \end{cases}](/forum/ext/geomar/texintegr/latexrender/pictures/f33a38035277ece5767168e19c7ea0de.png)
 είναι παραγωγίσιμη και συνεχής στο
είναι παραγωγίσιμη και συνεχής στο  ως διαφορά παραγωγίσιμων στο
ως διαφορά παραγωγίσιμων στο 
 .
. είναι συνεχής στο
είναι συνεχής στο ![[-\frac{\pi}{2}, \frac{\pi}{2}] [-\frac{\pi}{2}, \frac{\pi}{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/c48aa04a4a57f98397ce175c220a0c6f.png) ως σύνθεση συνεχών συναρτήσεων και επειδή:
ως σύνθεση συνεχών συναρτήσεων και επειδή:  και
και  (δεν έχω γράψει αναλυτικά τα όρια της
(δεν έχω γράψει αναλυτικά τα όρια της  ). Ταυτόχρονα, η
). Ταυτόχρονα, η  (δεν μας ενδιαφέρει τι γίνεται στο κλειστό διάστημα) ως σύνθεση παραγωγίσιμων συναρτήσεων σε κατάλληλα διαστήματα, με παράγωγο:
(δεν μας ενδιαφέρει τι γίνεται στο κλειστό διάστημα) ως σύνθεση παραγωγίσιμων συναρτήσεων σε κατάλληλα διαστήματα, με παράγωγο:  .
.![h(x)=0,\forall x\in [-\frac{\pi}{2}, \frac{\pi}{2}] h(x)=0,\forall x\in [-\frac{\pi}{2}, \frac{\pi}{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/6dd4cd2730d5217de7258b46eb4d14d1.png) .
. τέτοιο ώστε
τέτοιο ώστε  . Διακρίνουμε περιπτώσεις:
. Διακρίνουμε περιπτώσεις: , τότε:
, τότε: , άτοπο διότι
, άτοπο διότι  τέτοιο ώστε
τέτοιο ώστε ![h(x)\leq h(x_{max}), \forall x\in [-\frac{\pi}{2}, \frac{\pi}{2}] (4) h(x)\leq h(x_{max}), \forall x\in [-\frac{\pi}{2}, \frac{\pi}{2}] (4)](/forum/ext/geomar/texintegr/latexrender/pictures/a834407d78dbeb521fbe34938adc0556.png) . Σε αυτή τη σχέση αντικαθιστούμε
. Σε αυτή τη σχέση αντικαθιστούμε  οπότε
οπότε  άρα
άρα  .
. άρα λαμβάνοντας υπόψη τη σχέση (3) έχουμε:
άρα λαμβάνοντας υπόψη τη σχέση (3) έχουμε:  συνεπώς αντικαθιστούμε στη σχέση (2)
συνεπώς αντικαθιστούμε στη σχέση (2)  οπότε:
οπότε:  , άτοπο εξαιτίας της σχέσης (5).
, άτοπο εξαιτίας της σχέσης (5). , τότε όμοια έχουμε:
, τότε όμοια έχουμε: , άτοπο διότι
, άτοπο διότι  τέτοιο ώστε
τέτοιο ώστε ![h(x)\geq h(x_{min}), \forall x\in [-\frac{\pi}{2}, \frac{\pi}{2}] (6) h(x)\geq h(x_{min}), \forall x\in [-\frac{\pi}{2}, \frac{\pi}{2}] (6)](/forum/ext/geomar/texintegr/latexrender/pictures/aa7ab970c7aacc2797523ee2bc5d60b5.png) . Σε αυτή τη σχέση αντικαθιστούμε
. Σε αυτή τη σχέση αντικαθιστούμε  άρα
άρα  .
. άρα λαμβάνοντας υπόψη τη σχέση (3) έχουμε:
άρα λαμβάνοντας υπόψη τη σχέση (3) έχουμε:  συνεπώς αντικαθιστούμε στη σχέση (2)
συνεπώς αντικαθιστούμε στη σχέση (2)  οπότε:
οπότε:  , άτοπο εξαιτίας της σχέσης (7).
, άτοπο εξαιτίας της σχέσης (7). , ισχύει ότι:
, ισχύει ότι:  .
. .
. . Η
. Η  είναι συνεχής και γνησίως αύξουσα στο
είναι συνεχής και γνησίως αύξουσα στο  με
με  .
. το
το  για κάθε
για κάθε  ισχύει:
ισχύει:  και το ζητούμενο απεδείχθη.
και το ζητούμενο απεδείχθη. με την ισότητα μόνο για
με την ισότητα μόνο για  οπότε θέτοντας σε αυτή όπου
οπότε θέτοντας σε αυτή όπου  για κάθε
για κάθε  με την ισότητα μόνο για
με την ισότητα μόνο για  .
. οπότε θέτοντας όπου
οπότε θέτοντας όπου  το
το  για κάθε
για κάθε  με την ισότητα μόνο για
με την ισότητα μόνο για  .
. δηλαδή
δηλαδή  .
. θέτοντας όπου
θέτοντας όπου  για κάθε
για κάθε  δηλαδή
δηλαδή  , άρα, σύμφωνα με γνωστό πόρισμα του σχολικού βιβλίου,
, άρα, σύμφωνα με γνωστό πόρισμα του σχολικού βιβλίου,  οπότε πάλι σύμφωνα με θεώρημα του σχολικού βιβλίου (στα όρια)
οπότε πάλι σύμφωνα με θεώρημα του σχολικού βιβλίου (στα όρια)  επειδή το όριο υπάρχει σύμφωνα με την εκφώνηση.
επειδή το όριο υπάρχει σύμφωνα με την εκφώνηση. άρα (επειδή και τα δύο μέλη είναι θετικά)
άρα (επειδή και τα δύο μέλη είναι θετικά)  οπότε από το (β) προκύπτει ότι:
οπότε από το (β) προκύπτει ότι:  άρα σύμφωνα με γνωστό πόρισμα του σχολικού βιβλίου έχουμε:
άρα σύμφωνα με γνωστό πόρισμα του σχολικού βιβλίου έχουμε: ![\int\limits_{1}^{\lambda}{\left( \frac{1}{x^2}-f(x)\right) \, dx} > 0 \Rightarrow \int\limits_{1}^{\lambda}f(x)\, dx < \int\limits_{1}^{\lambda}\frac{1}{x^2}\, dx = \left[ -\frac{1}{x}\right]_{1}^{\lambda} = 1 - \frac{1}{\lambda} \int\limits_{1}^{\lambda}{\left( \frac{1}{x^2}-f(x)\right) \, dx} > 0 \Rightarrow \int\limits_{1}^{\lambda}f(x)\, dx < \int\limits_{1}^{\lambda}\frac{1}{x^2}\, dx = \left[ -\frac{1}{x}\right]_{1}^{\lambda} = 1 - \frac{1}{\lambda}](/forum/ext/geomar/texintegr/latexrender/pictures/e891de91244b8118b54b7dd1306ecedb.png) οπότε πάλι σύμφωνα με θεώρημα του σχολικού βιβλίου (στα όρια) είναι:
οπότε πάλι σύμφωνα με θεώρημα του σχολικού βιβλίου (στα όρια) είναι:  .
. , μπορούμε να το λάβουμε εκτός σχολικής ύλης με απευθείας ολοκλήρωση της σχέσης του (β) και τριγωνομετρική αντικατάσταση
, μπορούμε να το λάβουμε εκτός σχολικής ύλης με απευθείας ολοκλήρωση της σχέσης του (β) και τριγωνομετρική αντικατάσταση  στο ολοκλήρωμα που προκύπτει.
στο ολοκλήρωμα που προκύπτει. δεν χρειάζεται. Από τη λύση του gavrilos βλέπουμε ότι η
δεν χρειάζεται. Από τη λύση του gavrilos βλέπουμε ότι η  , αν δεν μηδενίζεται, είναι πάντα ετερόσημη με την παράγωγό της. Έτσι θα είναι ή θετική με αρνητική παράγωγο, ή αρνητική με θετική παράγωγο, ή μηδενική. Όπως είπε και ο gavrilos, τα δύο πρώτα έχουν άτοπο στο
, αν δεν μηδενίζεται, είναι πάντα ετερόσημη με την παράγωγό της. Έτσι θα είναι ή θετική με αρνητική παράγωγο, ή αρνητική με θετική παράγωγο, ή μηδενική. Όπως είπε και ο gavrilos, τα δύο πρώτα έχουν άτοπο στο  οπότε μένει μόνο το τρίτο.
οπότε μένει μόνο το τρίτο.