Ακριβώς. Όπως είπα δεν υπολόγισα το άθροισα-την διαφορά των κλασμάτων.Mihalis_Lambrou έγραψε:Και τώρα πες μου γιατί ο συλλογισμός αυτός έχει ένα σοβαρό λογικό σφάλμα.Eυ. N. έγραψε: Για το πρώτο :
Ας δούμε ένα παράδειγμα το οποίο ακολουθεί τον ίδιο (εσφαλμένο) συλλογισμό σου για να διαπιστώσουμε ότι κάτι δεν πάει καλά.
Πες ότι η εξίσωση έρχεται στην μορφή.
Με την ίδια λογική που έγραψες, θα είχαμε ότιδιαιρεί τον
.
Συμφωνούμε μέχρι εδώ;
Να όμως που η εξίσωση αυτή έχει λύση την(και άλλες) αλλά το
δεν διαιρεί το
.
Κάτι λοιπόν δεν πάει καλά με τον συλλογισμό σου.
Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Σε περίπτωση όμως που ήταν μόνο ένας όρος στο β'μέλος ο συλλογισμός θα ήταν σωστός.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Και εδώ που δεν είναι ένας όρος, ο συλλογισμός είναι λάθος.Eυ. N. έγραψε:Σε περίπτωση όμως που ήταν μόνο ένας όρος στο β'μέλος ο συλλογισμός θα ήταν σωστός.
Από κάτω γράφω σωστή λύση.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15762
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Ξεχάστηκε.ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ έγραψε:ΑΣΚΗΣΗ 552 (Βαθμός δυσκολίας 8, με κλίμακα από 1 έως 10). Να ΄λυθεί η εξίσωση:, με
Αφού πολλαπλασιάσουμε επί
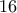 η εξίσωση παίρνει την μορφή
η εξίσωση παίρνει την μορφή
Οπότε οι παράγοντες αριστερά είναι διαιρέτες του
 και συγκεκριμένα έχουμε τις περιπτώσεις
και συγκεκριμένα έχουμε τις περιπτώσειςα)
 . Λύνοντας το γραμμικό σύστημα θα βρούμε
. Λύνοντας το γραμμικό σύστημα θα βρούμε  (δεκτή).
(δεκτή). β)
 . Θα βρούμε
. Θα βρούμε  (απορρίπτεται).
(απορρίπτεται).γ)
 . Θα βρούμε
. Θα βρούμε 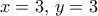 (δεκτή).
(δεκτή).Όμοια οι υπόλοιπες περιπτώσεις (στην πραγματικότητα μόνο αλλή μία, που όμως δεν δίνει λύση). Αφήνω τις πράξεις ρουτίνας.
-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4770
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
ΑΣΚΗΣΗ 591: (Βαθμός δυσκολίας 3, με κλίμακα από το 1 μέχρι το 10)
Δίνεται ισοσκελές τρίγωνο με κορυφή το
με κορυφή το  και έστω
και έστω  το ύψος του. Στην προέκταση της
το ύψος του. Στην προέκταση της  παίρνουμε το σημείο
παίρνουμε το σημείο  ,
,
ώστε να είναι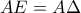 . Αν η
. Αν η 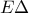 τέμνει την
τέμνει την  στο
στο  ,
,
(α) Να αποδείξετε ότι η ευθεία είναι κάθετη με την
είναι κάθετη με την 
(β) Να αποδείξετε ότι τα τρίγωνα και
και  είναι όμοια
είναι όμοια
(γ) Αν επί πλέον δίνεται ότι , να βρείτε τον λόγο
, να βρείτε τον λόγο  .
.
Δίνεται ισοσκελές τρίγωνο
 με κορυφή το
με κορυφή το  και έστω
και έστω  το ύψος του. Στην προέκταση της
το ύψος του. Στην προέκταση της  παίρνουμε το σημείο
παίρνουμε το σημείο  ,
, ώστε να είναι
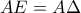 . Αν η
. Αν η 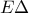 τέμνει την
τέμνει την  στο
στο  ,
,(α) Να αποδείξετε ότι η ευθεία
 είναι κάθετη με την
είναι κάθετη με την 
(β) Να αποδείξετε ότι τα τρίγωνα
 και
και  είναι όμοια
είναι όμοια(γ) Αν επί πλέον δίνεται ότι
 , να βρείτε τον λόγο
, να βρείτε τον λόγο  .
.Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Συγνώμη για το "εκτός θέματος" αλλά πώς μπορώ να πάρω την φωτογραφία, να την επεξεργαστώ και να την ξανανεβάσω στο φόρουμ.
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
ΑΣΚΗΣΗ 35
Ξεχάστηκε... ( δεν βρήκα κάπου λύση και έτσι γράφω την δική μου ).
Η παράσταση αυτή γράφεται :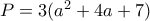 .
.
Όμως, . Όμως,
. Όμως,  και άρα αρκεί
και άρα αρκεί  .
.
Γνωρίζουμε όμως ότι, για περιττούς ισχύει
ισχύει  και άρα
και άρα  , το ζητούμενο.
, το ζητούμενο.
Ξεχάστηκε... ( δεν βρήκα κάπου λύση και έτσι γράφω την δική μου ).
Η παράσταση αυτή γράφεται :
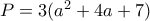 .
.Όμως,
 . Όμως,
. Όμως,  και άρα αρκεί
και άρα αρκεί  .
.Γνωρίζουμε όμως ότι, για περιττούς
 ισχύει
ισχύει  και άρα
και άρα  , το ζητούμενο.
, το ζητούμενο. Κερδίζουμε ό,τι τολμούμε!
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
ΑΣΚΗΣΗ 591
(α) Ας θέσουμε . Στο τρίγωνο
. Στο τρίγωνο 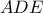 , η γωνία
, η γωνία  είναι εξωτερική και άρα
είναι εξωτερική και άρα  .
.
Όμως, , και άρα
, και άρα  , το ζητούμενο.
, το ζητούμενο.
(β) Τα τρίγωνα αυτά είναι όμοια, διότι έχουν μία ορθή γωνία( τις , αντίστοιχα ) και τις γωνίες
, αντίστοιχα ) και τις γωνίες  και
και  ίσες. Άρα είναι ισογώνια και το ζητούμενο έπεται.
ίσες. Άρα είναι ισογώνια και το ζητούμενο έπεται.
(γ) Θέτω . Άρα,
. Άρα,  . Οπότε, ο λόγος ομοιότητας
. Οπότε, ο λόγος ομοιότητας  είναι ίσος με
είναι ίσος με 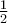 . Έτσι, ο λόγος των εμβαδών είναι
. Έτσι, ο λόγος των εμβαδών είναι  .
.
(α) Ας θέσουμε
 . Στο τρίγωνο
. Στο τρίγωνο 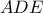 , η γωνία
, η γωνία  είναι εξωτερική και άρα
είναι εξωτερική και άρα  .
.Όμως,
 , και άρα
, και άρα  , το ζητούμενο.
, το ζητούμενο.(β) Τα τρίγωνα αυτά είναι όμοια, διότι έχουν μία ορθή γωνία( τις
 , αντίστοιχα ) και τις γωνίες
, αντίστοιχα ) και τις γωνίες  και
και  ίσες. Άρα είναι ισογώνια και το ζητούμενο έπεται.
ίσες. Άρα είναι ισογώνια και το ζητούμενο έπεται.(γ) Θέτω
 . Άρα,
. Άρα,  . Οπότε, ο λόγος ομοιότητας
. Οπότε, ο λόγος ομοιότητας  είναι ίσος με
είναι ίσος με 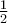 . Έτσι, ο λόγος των εμβαδών είναι
. Έτσι, ο λόγος των εμβαδών είναι  .
.
τελευταία επεξεργασία από Ορέστης Λιγνός σε Παρ Ιουν 03, 2016 11:51 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Κερδίζουμε ό,τι τολμούμε!
-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4770
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Νομίζω ότι είναι εύκολο να το φτιάξεις στο Geogebra, να το μεταφέρεις πάνω δεξιά, να το βάλεις (πατώντας δεξί κλικ) σε πλαίσιο, να πας "αρχείο", εξαγωγή, Προβολή γραφικών ως εικόνα , Αποθήκευση (στην επιφάνεια εργασίας).Silver έγραψε:Συγνώμη για το "εκτός θέματος" αλλά πώς μπορώ να πάρω την φωτογραφία, να την επεξεργαστώ και να την ξανανεβάσω στο φόρουμ.
Μετά για να το ανεβάσεις εδώ, βρες και πάτα Προσθήκη συνημμένου, επιλογή αρχείου, επέλεξε το από την επιφάνεια εργασίας, μετά πάτα προσθήκη αρχείου και μετά προβολή στην δημοσίευση.
τελευταία επεξεργασία από ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ σε Τρί Ιουν 07, 2016 10:12 pm, έχει επεξεργασθεί 1 φορά συνολικά.
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Επαναφέρω την ΑΣΚΗΣΗ 557. Έχω μερικές σκέψεις, αλλά αύριο θα ασχοληθώ σοβαρά με την άσκηση λόγω του περασμένου της ώρας.
Κερδίζουμε ό,τι τολμούμε!
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
(α) Λύνοντας την διτετράγωνη εξίσωση που προκύπτει λαμβάνουμε  .
.
(β) Δεν υπάρχουν, γιατί το είναι πάντα άρτιος, ανεξάρτητα από την αρτιοπεριττότητα του
είναι πάντα άρτιος, ανεξάρτητα από την αρτιοπεριττότητα του  . Όμως, το
. Όμως, το  είναι περιττός.
είναι περιττός.
(γ) Απλώς, το παραγοντοποιείται ως
παραγοντοποιείται ως  , το οποίο, ως γινόμενο δύο αριθμών διάφορων του
, το οποίο, ως γινόμενο δύο αριθμών διάφορων του  δεν είναι πρώτος.( τα
δεν είναι πρώτος.( τα  ,
,  είναι προφανώς
είναι προφανώς  , διότι, αν κάποιο ήταν
, διότι, αν κάποιο ήταν  , θα είχαμε εύκολα
, θα είχαμε εύκολα  ή
ή  , με τις δύο περιπτώσεις να είναι προφανώς αδύνατες. μιας και
, με τις δύο περιπτώσεις να είναι προφανώς αδύνατες. μιας και  .).
.).
Τα υπόλοιπα αύριο...
 .
.(β) Δεν υπάρχουν, γιατί το
 είναι πάντα άρτιος, ανεξάρτητα από την αρτιοπεριττότητα του
είναι πάντα άρτιος, ανεξάρτητα από την αρτιοπεριττότητα του  . Όμως, το
. Όμως, το  είναι περιττός.
είναι περιττός.(γ) Απλώς, το
 παραγοντοποιείται ως
παραγοντοποιείται ως  , το οποίο, ως γινόμενο δύο αριθμών διάφορων του
, το οποίο, ως γινόμενο δύο αριθμών διάφορων του  δεν είναι πρώτος.( τα
δεν είναι πρώτος.( τα  ,
,  είναι προφανώς
είναι προφανώς  , διότι, αν κάποιο ήταν
, διότι, αν κάποιο ήταν  , θα είχαμε εύκολα
, θα είχαμε εύκολα  ή
ή  , με τις δύο περιπτώσεις να είναι προφανώς αδύνατες. μιας και
, με τις δύο περιπτώσεις να είναι προφανώς αδύνατες. μιας και  .).
.).Τα υπόλοιπα αύριο...
Κερδίζουμε ό,τι τολμούμε!
-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4770
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
ΑΣΚΗΣΗ 592: (Βαθμός δυσκολίας 6, με κλίμακα από 1 μέχρι 10)
Αν , να αποδείξετε ότι
, να αποδείξετε ότι 
Αν
 , να αποδείξετε ότι
, να αποδείξετε ότι 
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Μία λύση με πολλές, πολλές πράξεις.ΔΗΜΗΤΡΗΣ έγραψε:ΑΣΚΗΣΗ 592: (Βαθμός δυσκολίας 6, με κλίμακα από 1 μέχρι 10)
Αν, να αποδείξετε ότι
Εξισώνοντας την δεύτερη με την τρίτη σχέση λαμβάνουμε ότι
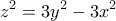 (1).
(1).Εξισώνοντας τώρα την πρώτη με την δεύτερη σχέση και χρησιμοποιώντας την (1), παίρνουμε ότι
 .
.Ομοίως, με την πρώτη και την τρίτη σχέση είναι
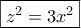 .
.Έχουμε τώρα τέσσερις περιπτώσεις
1)

2)
 κλπ
κλπΑς δούμε την πρώτη περίπτωση. Εξισώνοντας πρώτη και τέταρτη σχέση και χρησιμοποιώντας τις σχέσεις
 , παίρνουμε ότι
, παίρνουμε ότι  . Ο αριθμός στην παρένθεση είναι προφανώς διάφορος του μηδέν, αφού
. Ο αριθμός στην παρένθεση είναι προφανώς διάφορος του μηδέν, αφού  ενώ το
ενώ το  είναι άρρητος.
είναι άρρητος.Συνεπώς,
 και εύκολα
και εύκολα  , που είναι και το ζητούμενο.
, που είναι και το ζητούμενο.Ομοίως και οι υπόλοιπες περιπτώσεις.
Κερδίζουμε ό,τι τολμούμε!
-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4770
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Ωραιότατα Ορέστη!!!orestis26 έγραψε:Μία λύση με πολλές, πολλές πράξεις.ΔΗΜΗΤΡΗΣ έγραψε:ΑΣΚΗΣΗ 592: (Βαθμός δυσκολίας 6, με κλίμακα από 1 μέχρι 10)
Αν, να αποδείξετε ότι
Εξισώνοντας την δεύτερη με την τρίτη σχέση λαμβάνουμε ότι(1).
Εξισώνοντας τώρα την πρώτη με την δεύτερη σχέση και χρησιμοποιώντας την (1), παίρνουμε ότι.
Ομοίως, με την πρώτη και την τρίτη σχέση είναι.
Έχουμε τώρα τέσσερις περιπτώσεις
1)
2)κλπ
Ας δούμε την πρώτη περίπτωση. Εξισώνοντας πρώτη και τέταρτη σχέση και χρησιμοποιώντας τις σχέσεις, παίρνουμε ότι
. Ο αριθμός στην παρένθεση είναι προφανώς διάφορος του μηδέν, αφού
ενώ το
είναι άρρητος.
Συνεπώς,και εύκολα
, που είναι και το ζητούμενο.
Ομοίως και οι υπόλοιπες περιπτώσεις.
Ας δούμε και μια ακόμα λύση: Έχουμε:
 , (1)
, (1)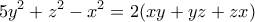
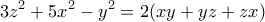
Με πρόσθεση κατά μέλη των πιο πάνω εξισώσεων, παίρνουμε:

 . Άρα
. Άρα 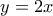 και
και  , δηλαδή
, δηλαδή 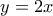 και
και  .
. Τώρα η (1) γράφεται

Άρα
 (που επαληθεύουν και τις αρχικές συνθήκες)
(που επαληθεύουν και τις αρχικές συνθήκες)-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4770
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
- Ορέστης Λιγνός
- Δημοσιεύσεις: 1835
- Εγγραφή: Κυρ Μάιος 08, 2016 7:19 pm
- Τοποθεσία: Χαλάνδρι Αττικής
- Επικοινωνία:
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Καλησπέρα!ΔΗΜΗΤΡΗΣ έγραψε:ΑΣΚΗΣΗ 593: Να λυθεί το σύστημα:
Προσθέτοντας κατά μέλη λαμβάνουμε
 .
.Αυτή γράφεται
 . από όπου έχουμε την λύση
. από όπου έχουμε την λύση  , η οποία όμως δεν επαληθεύει τις αρχικές εξισώσεις και άρα απορρίπτεται.
, η οποία όμως δεν επαληθεύει τις αρχικές εξισώσεις και άρα απορρίπτεται.Υ.Γ. Δεν ξέρω αν είμαι σωστός στις πράξεις.Είναι και η μεσημεριανή ξεκούραση...
Φιλικά,
Ορέστης.
τελευταία επεξεργασία από Ορέστης Λιγνός σε Πέμ Ιουν 16, 2016 3:03 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Κερδίζουμε ό,τι τολμούμε!
-
ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ
- Δημοσιεύσεις: 3600
- Εγγραφή: Πέμ Φεβ 27, 2014 9:05 am
- Τοποθεσία: ΧΑΛΚΙΔΑ- ΑΘΗΝΑ-ΚΡΗΤΗ
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Για την ΑΣΚΗΣΗ 593
Πιστεύω ότι υπάρχει τυπογραφικό.
Η δεύτερη εξίσωση είναι αδύνατη στους πραγματικούς.
Πιστεύω ότι υπάρχει τυπογραφικό.
Η δεύτερη εξίσωση είναι αδύνατη στους πραγματικούς.
-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4770
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
Όχι Σταύρο, δεν υπάρχει τυπογραφικό. Η ιδέα της κατασκευής ήταν να λυθεί με τον τρόπο που έκανε ο Ορέστης και ύστερα όμως να γίνει οπωσδήποτε η επαλήθευση. Τώρα βέβαια, πολύ καλά παρατήρησες ότι έβγαινε αδύνατο και μόνο από την δεύτερη εξίσωση, οπότε και πάλι είναι αδύνατο το σύστημα. Αυτό θα μπορούσε να διορθωθεί , αν το σύστημα δινόταν π.χ ως εξής:ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε:Για την ΑΣΚΗΣΗ 593
Πιστεύω ότι υπάρχει τυπογραφικό.
Η δεύτερη εξίσωση είναι αδύνατη στους πραγματικούς.



Τότε με τον τρόπο που έκανε ο Ορέστης, λύνεται εύκολα.
-
ΔΗΜΗΤΡΗΣ ΙΩΑΝΝΟΥ
- Επιμελητής
- Δημοσιεύσεις: 4770
- Εγγραφή: Τρί Αύγ 31, 2010 10:37 pm
- Τοποθεσία: Ιστιαία Ευβοίας
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
ΑΣΚΗΣΗ 594: (Βαθμός δυσκολίας 3, με κλίμακα από το 1 μέχρι το 10) . Αν ο αριθμός 
δεν διαιρείται με το , να βρεθεί ο μη αρνητικός ακέραιος αριθμός
, να βρεθεί ο μη αρνητικός ακέραιος αριθμός 

δεν διαιρείται με το
 , να βρεθεί ο μη αρνητικός ακέραιος αριθμός
, να βρεθεί ο μη αρνητικός ακέραιος αριθμός 
-
papamixalis
- Δημοσιεύσεις: 200
- Εγγραφή: Σάβ Ιουν 13, 2015 3:38 pm
Re: Εισαγωγή σε Διαγωνιστικά Μαθηματικά για Γυμνάσιο
594 μια προσπάθεια.αν κάνουμε τις πράξεις καταλήγουμε στο  όλοι οι όροι διαιρούνται με το
όλοι οι όροι διαιρούνται με το  Εκτός εαν
Εκτός εαν 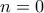
 όλοι οι όροι διαιρούνται με το
όλοι οι όροι διαιρούνται με το  Εκτός εαν
Εκτός εαν 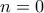
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης





