Ο λεπτοδείκτης διαγράφει σε μία ώρα (60 λεπτά) γωνίαΠαύλος Μαραγκουδάκης έγραψε:ΠΡΟΒΛΗΜΑ 22
Ποια στιγμή, ανάμεσα στις εννέα και δέκα η ώρα, οι δείκτες ενός ρολογιού είναι μαζί;
 , άρα σε 1 λεπτό διαγράφει γωνία
, άρα σε 1 λεπτό διαγράφει γωνία  . Αντίστοιχα ο ωροδείκτης σε μία ώρα διαγράφει γωνία
. Αντίστοιχα ο ωροδείκτης σε μία ώρα διαγράφει γωνία  , άρα σε 1 λεπτό διαγράφει γωνία
, άρα σε 1 λεπτό διαγράφει γωνία  .
.Έστω ότι οι δείκτες θα συμπέσουν σε
 λεπτά. Τότε ο λεπτοδείκτης θα έχει διαγράψει γωνία
λεπτά. Τότε ο λεπτοδείκτης θα έχει διαγράψει γωνία  και αντίστοιχα ο ωροδείκτης γωνία
και αντίστοιχα ο ωροδείκτης γωνία  .
.Αλλά,

 λεπτά και
λεπτά και  του δευτερολέπτου.
του δευτερολέπτου.Οι δείκτες λοιπόν θα συμπέσουν στις
 και
και  του δευτερολέπτου.
του δευτερολέπτου.
 μέχρι
μέχρι  ) ,
) , 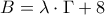 , όπου
, όπου  ο βαθμός ,
ο βαθμός ,  ένας συντελεστής και
ένας συντελεστής και  ο βαθμός του γραπτού .
ο βαθμός του γραπτού . ?
?

 ,
, 
 .
. 




 και μετά πολλαπλάσια του
και μετά πολλαπλάσια του  θα πάρει ο καθένας από
θα πάρει ο καθένας από  μήλα.Δηλαδή μείναν
μήλα.Δηλαδή μείναν  για να εχουν ίδιο αριθμό μήλων με τον πρώτο
για να εχουν ίδιο αριθμό μήλων με τον πρώτο ενός αριθμού προσθέσουμε τον αριθμό 2 , και στο αποτέλεσμα αυτό αφαιρέσουμε το
ενός αριθμού προσθέσουμε τον αριθμό 2 , και στο αποτέλεσμα αυτό αφαιρέσουμε το 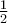 του αριθμού αυξημένο κατα 6 βρίσκουμε το
του αριθμού αυξημένο κατα 6 βρίσκουμε το  του αριθμού ελλατωμένο κατα 3. Να βρεθεί ο αριθμός αυτός εάν γνωρίζουμε οτι είναι πολλαπλάσιο του 9 και περιέχεται μεταξύ των 50 και 80.
του αριθμού ελλατωμένο κατα 3. Να βρεθεί ο αριθμός αυτός εάν γνωρίζουμε οτι είναι πολλαπλάσιο του 9 και περιέχεται μεταξύ των 50 και 80.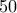 σκαλιά. Μετά ανέβηκε την ίδια σκάλα πάλι σκαλί σκαλί και πέρασε από
σκαλιά. Μετά ανέβηκε την ίδια σκάλα πάλι σκαλί σκαλί και πέρασε από  σκαλιά. Υποθέτοντας ότι έκανε
σκαλιά. Υποθέτοντας ότι έκανε  όταν κατέβαινε, πόσα σκαλιά θα βλέπαμε αν σταματούσε η κυλιόμενη σκάλα; Οι ταχύτητες με τις οποίες ανέβηκε και κατέβηκε ήταν σταθερές.
όταν κατέβαινε, πόσα σκαλιά θα βλέπαμε αν σταματούσε η κυλιόμενη σκάλα; Οι ταχύτητες με τις οποίες ανέβηκε και κατέβηκε ήταν σταθερές. σκαλοπάτια . Σε καθένα λοιπόν βήμα προς τα κάτω ''χάνονται''
σκαλοπάτια . Σε καθένα λοιπόν βήμα προς τα κάτω ''χάνονται''  σκαλοπάτια .
σκαλοπάτια . σκαλοπάτια . Σε καθένα λοιπόν βήμα προς τα πάνω ''χάνονται''
σκαλοπάτια . Σε καθένα λοιπόν βήμα προς τα πάνω ''χάνονται''  σκαλοπάτια .
σκαλοπάτια .




 σκαλοπάτια .
σκαλοπάτια . γνωρίζουμε ότι η γωνία
γνωρίζουμε ότι η γωνία  είναι διπλάσια της γωνίας
είναι διπλάσια της γωνίας  Σχεδιάζουμε τις διχοτόμους
Σχεδιάζουμε τις διχοτόμους  του τριγώνου και ονομάζουμε
του τριγώνου και ονομάζουμε  το σημείο τομής τους. Γνωρίζουμε ακόμα ότι
το σημείο τομής τους. Γνωρίζουμε ακόμα ότι  Να βρείτε τις γωνίες του τριγώνου
Να βρείτε τις γωνίες του τριγώνου 
 και
και 
 θα πάρουμε την εξίσωση (που προκύπτει με την βοήθεια των διχοτόμων):
θα πάρουμε την εξίσωση (που προκύπτει με την βοήθεια των διχοτόμων):









 Γνωρίζουμε ακόμα ότι
Γνωρίζουμε ακόμα ότι  Να βρείτε τις γωνίες του τριγώνου
Να βρείτε τις γωνίες του τριγώνου  ως παραπληρωματικές με την
ως παραπληρωματικές με την 

 και
και  αν ονομάσουμε
αν ονομάσουμε  και
και 

 :
:







 που έχει
που έχει  και
και  . Έστω
. Έστω  το μέσον της
το μέσον της  και
και  το μέσον της
το μέσον της  .
.  , σαν συνάρτηση του
, σαν συνάρτηση του  .
.
 . Τώρα:
. Τώρα:




 ,
,  ,
,  θα λάβουμε:
θα λάβουμε:


 η περίμετρος του τριγώνου θα ισχύει:
η περίμετρος του τριγώνου θα ισχύει:





 λεπτά και
λεπτά και  του δευτερολέπτου .
του δευτερολέπτου . και πάνω στην προέκταση της
και πάνω στην προέκταση της  και προς το μέρος του
και προς το μέρος του  παίρνουμε ένα
παίρνουμε ένα  έτσι ώστε να είναι
έτσι ώστε να είναι  . Αν η γωνία
. Αν η γωνία  , να υπολογίσετε το μέτρο της γωνίας
, να υπολογίσετε το μέτρο της γωνίας 
 τότε
τότε  . Οπότε:
. Οπότε:  και
και  .
. έχουμε:
έχουμε: 




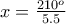

 λεπτά και
λεπτά και  του δευτερολέπτου .
του δευτερολέπτου .


 η εξίσωση αληθεύει για κάθε πραγματικό αριθμό , δηλ. είναι ταυτότητα .
η εξίσωση αληθεύει για κάθε πραγματικό αριθμό , δηλ. είναι ταυτότητα . ή
ή  ή
ή  .
. μ. και θέλει να κατασκευάσει ένα ορθογώνιο πλαίσιο με αναλογίες χρυσής τομής . Μπορείτε να βοηθήσετε τον μαραγκό να βρει τις διαστάσεις του ορθογωνίου με προσέγγιση χιλιοστού; Δίνεται ο αριθμός της χρυσής τομής φ=
μ. και θέλει να κατασκευάσει ένα ορθογώνιο πλαίσιο με αναλογίες χρυσής τομής . Μπορείτε να βοηθήσετε τον μαραγκό να βρει τις διαστάσεις του ορθογωνίου με προσέγγιση χιλιοστού; Δίνεται ο αριθμός της χρυσής τομής φ= .
. οι πλευρές του ορθογωνίου με
οι πλευρές του ορθογωνίου με 



 το πλάτος του με
το πλάτος του με 
 έχουμε
έχουμε 

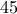 , μιας και είμαστε σε περίοδο οικονομικής κρίσης και τίποτα δεν πρέπει να χάνεται, πόσο μάλλον να ξοδεύεται...
, μιας και είμαστε σε περίοδο οικονομικής κρίσης και τίποτα δεν πρέπει να χάνεται, πόσο μάλλον να ξοδεύεται... μεγαλύτερη από του Μπάμπη, ενώ ο Μπάμπης χάνει στη θάλασσα τα
μεγαλύτερη από του Μπάμπη, ενώ ο Μπάμπης χάνει στη θάλασσα τα 
 της δικής του. Μόλις φτάνουν κι οι δύο στο νησί, υπολογίζουν το συνολικό διάστημα που καθένας διάνυσε (σε στεριά και θάλασσα) και διαπιστώνουν ότι είναι συνολικά σο ίδιο και για τους δυο. Να βρεθεί η γωνία που σχηματίζει η ευθεία στην οποία κολύμπησε ο Νώντας με τη νοητή ευθεία της ακτής. (Ο Μπάμπης κολύμπησε κάθετα προς την ακτή).
της δικής του. Μόλις φτάνουν κι οι δύο στο νησί, υπολογίζουν το συνολικό διάστημα που καθένας διάνυσε (σε στεριά και θάλασσα) και διαπιστώνουν ότι είναι συνολικά σο ίδιο και για τους δυο. Να βρεθεί η γωνία που σχηματίζει η ευθεία στην οποία κολύμπησε ο Νώντας με τη νοητή ευθεία της ακτής. (Ο Μπάμπης κολύμπησε κάθετα προς την ακτή). διάστημα
διάστημα 
 η ταχύτητα του Μπάμπη στη στεριά. Τότε η ταχύτητα του Μπάμπη στη θάλασσα θα είναι
η ταχύτητα του Μπάμπη στη στεριά. Τότε η ταχύτητα του Μπάμπη στη θάλασσα θα είναι 
 μεγαλύτερη στη στεριά, δηλαδή είναι
μεγαλύτερη στη στεριά, δηλαδή είναι  ενώ στη θάλασσα είναι
ενώ στη θάλασσα είναι 
 και στη θάλασσα
και στη θάλασσα  μέτρα.
μέτρα. και στη θάλασσα
και στη θάλασσα  μέτρα. To συνολικό διάστημα είναι το ίδιο και για τους δύο, άρα οδηγούμαστε στην εξίσωση
μέτρα. To συνολικό διάστημα είναι το ίδιο και για τους δύο, άρα οδηγούμαστε στην εξίσωση 

 του νησιού ενώ ο Νώντας στο σημείο
του νησιού ενώ ο Νώντας στο σημείο  Αν
Αν  μέτρα
μέτρα  μέτρα.
μέτρα. είναι
είναι  οπότε η ζητούμενη γωνία είναι
οπότε η ζητούμενη γωνία είναι 