exdx έγραψε:Άσκηση 21
Εύκολη - απαιτούνται γνώσεις Β΄ Γυμνασίου
Μια διαδικασία ολοκληρώνεται από τον Α σε

ώρες , από τον Β σε
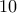
ώρες και από τον Γ σε

ώρες .
Αν εργαστούν και οι τρεις μαζί σε πόσες ώρες θα την ολοκληρώσουν ;
Έστω ότι η διαδικασία θα ολοκληρωθεί σε

ώρες. Τότε σε

ώρα , ο

, θα έχει εκτελέσει τα

της διαδικασίας, ο

τα

και ο

, τα

της διαδικασίας. Επομένως, μέσα σε μια ώρα, και οι τρεις μαζί, θα έχουνε εκτελέσει τα

της διαδικασίας, δηλαδή τα

της διαδικασίας.
Επομένως, μέσα σε μια ώρα, θα έχει εκτελεστεί η μισή διαδικασία και άρα ολόκληρη θα εκτελεστεί μέσα σε

ώρες.
Edit: Διόρθωσα μια λανθασμένη διατύπωση που μου την είπε ο gauss1988
 ΠΑΡΟΜΟΙΑ ΜΕ ΑΥΤΟ ΤΟ ΠΡΟΒΛΗΜΑ ΕΙΝΑΙ ΚΑΙ ΤΑ ΕΠΟΜΕΝΑ:
ΠΡΟΒΛΗΜΑ 22.
ΠΑΡΟΜΟΙΑ ΜΕ ΑΥΤΟ ΤΟ ΠΡΟΒΛΗΜΑ ΕΙΝΑΙ ΚΑΙ ΤΑ ΕΠΟΜΕΝΑ:
ΠΡΟΒΛΗΜΑ 22. Μια βρύση, γεμίζει μια δεξαμενή σε

ώρες. Μια άλλη σε

ώρες. Και οι δύο μαζί σε πόσες ώρες θα την γεμίσουν;
ΠΡΟΒΛΗΜΑ 23. Μια βρύση, γεμίζει μια δεξαμενή σε

ώρες. Μια άλλη, που είναι στο κάτω μέρος της δεξαμενής, μπορεί να την αδειάσει σε

ώρες. Άμα ανοιχτούνε και οι δύο μαζί, σε πόση ώρα θα γεμίσει η δαξαμενή;
ΠΡΟΒΛΗΜΑ 24. Σε κυλιόμενες σκάλες ενός πολυκαταστήματος, ένας πελάτης, άμα σταθεί ακίνητος, ανεβάίνει σε

λεπτά.
Άμα όμως έχει κοπεί το ρεύμα, παρατήρησε ότι ανεβαίνει σε

λεπτά. Πόσο χρόνο θα χρειαστεί να ανέβει, όταν και ο ίδιος ανεβαίνει αλλά και οι σκάλες λειτουργούνε;
που ικανοποιούν τη σχέση
και αφού
τα πράγματα είναι απλά.
 :αυτό πως το παρατήρησες;
:αυτό πως το παρατήρησες;

 εμφανίζονται το άθροισμα,τα διπλάσια γινόμενα των 3 μεταβήτών και το γινόμενο τους και έτσι το πρόβλημα αναχθηκέ στην αναζήτηση του
εμφανίζονται το άθροισμα,τα διπλάσια γινόμενα των 3 μεταβήτών και το γινόμενο τους και έτσι το πρόβλημα αναχθηκέ στην αναζήτηση του  που στην προκειμένη είναι πολύ απλό.
που στην προκειμένη είναι πολύ απλό.

![\displaystyle{\Leftrightarrow (z-2)[x(y-2)-2(y-2)]=-1\Leftrightarrow (z-2)(y-2)(x-2)=-1} \displaystyle{\Leftrightarrow (z-2)[x(y-2)-2(y-2)]=-1\Leftrightarrow (z-2)(y-2)(x-2)=-1}](/forum/ext/geomar/texintegr/latexrender/pictures/2303884eeda741b01c09abf49f77fe73.png)
 , ή
, ή , ή........ κλπ
, ή........ κλπ , ή
, ή  , ή ,
, ή ,  , ή
, ή 

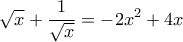 . Επειδή
. Επειδή 
 ( θυμηθείτε
( θυμηθείτε  ), ενώ το τριώνυμο του β' μέλους έχει μέγιστη τιμή
), ενώ το τριώνυμο του β' μέλους έχει μέγιστη τιμή  για
για  ( θυμηθείτε την κορυφή της παραβολής που είναι η γρ. παράσταση του τριωνύμου ).
( θυμηθείτε την κορυφή της παραβολής που είναι η γρ. παράσταση του τριωνύμου ).  ώρες , από τον Β σε
ώρες , από τον Β σε 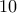 ώρες και από τον Γ σε
ώρες και από τον Γ σε  ώρες .
ώρες . είιναι αρκετά δύσκολη για κάποιον που δεν είναι εξικοιωμένος με την παραγοντοποίηση όμως δεν χρειάζεται καμία επιπλέον γνώση εκτός αυτής της παραγοντοποίησης.Ο Κλεόβουλος είπε σαφέστατα ότι θέλει να ξέρει την θεωρία και τίποτα παραπάνω.Δεν μπορώ να καταλάβω το ύφος της απάντησης σου karanus.
είιναι αρκετά δύσκολη για κάποιον που δεν είναι εξικοιωμένος με την παραγοντοποίηση όμως δεν χρειάζεται καμία επιπλέον γνώση εκτός αυτής της παραγοντοποίησης.Ο Κλεόβουλος είπε σαφέστατα ότι θέλει να ξέρει την θεωρία και τίποτα παραπάνω.Δεν μπορώ να καταλάβω το ύφος της απάντησης σου karanus. ώρες. Τότε σε
ώρες. Τότε σε  ώρα , ο
ώρα , ο  , θα έχει εκτελέσει τα
, θα έχει εκτελέσει τα  της διαδικασίας, ο
της διαδικασίας, ο  τα
τα  και ο
και ο  , τα
, τα  της διαδικασίας. Επομένως, μέσα σε μια ώρα, και οι τρεις μαζί, θα έχουνε εκτελέσει τα
της διαδικασίας. Επομένως, μέσα σε μια ώρα, και οι τρεις μαζί, θα έχουνε εκτελέσει τα  της διαδικασίας, δηλαδή τα
της διαδικασίας, δηλαδή τα  της διαδικασίας.
της διαδικασίας.  ώρες. Μια άλλη σε
ώρες. Μια άλλη σε  ώρες. Και οι δύο μαζί σε πόσες ώρες θα την γεμίσουν;
ώρες. Και οι δύο μαζί σε πόσες ώρες θα την γεμίσουν; ώρες. Μια άλλη, που είναι στο κάτω μέρος της δεξαμενής, μπορεί να την αδειάσει σε
ώρες. Μια άλλη, που είναι στο κάτω μέρος της δεξαμενής, μπορεί να την αδειάσει σε  λεπτά. Πόσο χρόνο θα χρειαστεί να ανέβει, όταν και ο ίδιος ανεβαίνει αλλά και οι σκάλες λειτουργούνε;
λεπτά. Πόσο χρόνο θα χρειαστεί να ανέβει, όταν και ο ίδιος ανεβαίνει αλλά και οι σκάλες λειτουργούνε; είναι διάφοροι του μηδενός και αν
είναι διάφοροι του μηδενός και αν  , να υπολογίσετε την αριθμητική τιμή της παράσρασης:
, να υπολογίσετε την αριθμητική τιμή της παράσρασης: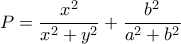
 . Σε καθένα τώρα από τα κλάσματα της παράστασης
. Σε καθένα τώρα από τα κλάσματα της παράστασης  , προσπαθήστε να εμφανίσετε τους λόγους
, προσπαθήστε να εμφανίσετε τους λόγους 
 της δεξαμενής.
της δεξαμενής. αυτής. Άρα για να βρω το
αυτής. Άρα για να βρω το  , από όπου προκύπτει
, από όπου προκύπτει  ώρες.
ώρες. , από όπου προκύπτει
, από όπου προκύπτει  ώρες.
ώρες. , απ'ο 'οπου
, απ'ο 'οπου  λεπτ'α.
λεπτ'α.

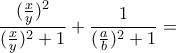

 , με
, με  , θεωρούμε σημείο
, θεωρούμε σημείο  στην βάση
στην βάση  και σημείο
και σημείο  στην πλευρά
στην πλευρά  , έτσι ώστε η γωνία
, έτσι ώστε η γωνία  να ισούται με το διπλάσιο της γωνίας
να ισούται με το διπλάσιο της γωνίας  .
. .
. , με άγνωστο τον πραγματικό αριθμό
, με άγνωστο τον πραγματικό αριθμό  .
. . Επομένως, πρέπει να αποδείξω ότι οι γωνίες
. Επομένως, πρέπει να αποδείξω ότι οι γωνίες  και
και  είναι ίσες.
είναι ίσες. και επομένως, θα ισούται με το άθροισμα των απέναντι εσωτερικών γωνιών του. Δηλαδή,
και επομένως, θα ισούται με το άθροισμα των απέναντι εσωτερικών γωνιών του. Δηλαδή,  (i)
(i) , είναι εξωτερική στο τρίγωνο
, είναι εξωτερική στο τρίγωνο  , και επομένως,
, και επομένως,  , δηλ.
, δηλ.  (ii)
(ii)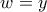 , δηλ.
, δηλ.  είναι τέλειοι κύβοι, να αποδειχθεί ότι και οι φυσικοί αριθμοί
είναι τέλειοι κύβοι, να αποδειχθεί ότι και οι φυσικοί αριθμοί  είναι τέλειοι κύβοι.
είναι τέλειοι κύβοι. ακέραιοι αριθμοί, έτσι ώστε οι αριθμοί
ακέραιοι αριθμοί, έτσι ώστε οι αριθμοί  να είναι διαδοχικοί ακέραιοι. Να αποδείξετε ότι ο
να είναι διαδοχικοί ακέραιοι. Να αποδείξετε ότι ο  είναι τέλειο τετράγωνο.
είναι τέλειο τετράγωνο. και έχουμε ότι :
και έχουμε ότι :