Ολοκλήρωμα με λογάριθμο και ημίτονα

#1

Ας υπολογισθεί το $\displaystyle{\int_{0}^{\pi/4}\ln\left(\frac{1+\sin x}{1-\sin x}\right)\,dx}$ .

S.E.Louridas · #2

Αναστάση αν το ολοκλήρωμα το ονομάσουμε

και λαμβάνοντας υπ’ όψιν συζυγείς παραστάσεις κ.τ.λ. και με κάθε επιφύλλαξη λόγω κάποιων "διαισθητικών μείον" γιά την συνέχεια, έχουμε:

$\begin{array}{*{20}c} {I = \int\limits_0^{\frac{\pi } {4}} {\ln \frac{{\left( {1 + \sin x} \right)^2 }} {{\cos ^2 x}}dx = 2\int\limits_0^{\frac{\pi } {4}} {\ln \left( {1 + \sin x} \right)dx - 2\int\limits_0^{\frac{\pi } {4}} {\ln \left( {\cos x} \right)dx = } } } } \\ {4\int\limits_0^{\frac{\pi } {4}} {\ln \left( {\sin \frac{x} {2} + \sin \left( {\frac{\pi } {2} - \frac{x} {2}} \right)} \right)dx - 2\int\limits_0^{\frac{\pi } {4}} {\ln \left( {\cos x} \right)dx = } \frac{\pi } {2}\ln 2 + 4\int\limits_0^{\frac{\pi } {4}} {\ln \cos \left( {\frac{x} {2} - \frac{\pi } {4}} \right)dx - } } } \\ {2\int\limits_0^{\frac{\pi } {4}} {\ln \left( {\cos x} \right)dx = \frac{\pi } {2}\ln 2 + 8\int\limits_{ - \frac{\pi } {4}}^{ - \frac{\pi } {8}} {\ln \left( {\cos x} \right)dx - 2\int\limits_0^{\frac{\pi } {4}} {\ln \left( {\cos x} \right)dx = } } ...} } \\ \end{array}$

S.E.Louridas

#3

και μετά; Τα δυο τελευταία ολοκληρώματα είναι πολύ ζόρικα και βγαίνουν συναρτήσει του αριθμού Catalan. Το γνωστό που έχουμε ξανασυζητήσει είναι σε διάστημα ολοκλήρωσης μήκους $\pi/2$ .

S.E.Louridas · #4

S.E.Louridas έγραψε:.... και με κάθε επιφύλλαξη λόγω κάποιων "διαισθητικών μείον" γιά την συνέχεια, έχουμε:...

Αναστάση είδωμεν

S.E.Louridas

#5

$\displaystyle{\int\limits_0^{\pi /4} {\ln \left( {\frac{{1 + \sin \left( x \right)}}{{1 - \sin \left( x \right)}}} \right)dx} = \mathop = \limits^{x = \pi /2 - y} = \int\limits_{\pi /4}^{\pi /2} {\ln \left( {\frac{{1 + \cos \left( y \right)}}{{1 - \cos \left( y \right)}}} \right)dy} = \int\limits_{\pi /4}^{\pi /2} {\ln \left( {\frac{{2{{\cos }^2}\left( {y/2} \right)}}{{2{{\sin }^2}\left( {y/2} \right)}}} \right)dy} = - 2\int\limits_{\pi /4}^{\pi /2} {\ln \left( {\tan \left( {y/2} \right)} \right)dy} = }$

$\displaystyle{ = \mathop = \limits^{y/2 = x} = - 4\int\limits_{\pi /8}^{\pi /4} {\ln \left( {\tan \left( x \right)} \right)dx} = \mathop = \limits^{\tan \left( x \right) = y} = - 4\int\limits_{\sqrt 2 - 1}^1 {\frac{{\ln \left( y \right)}}{{1 + {y^2}}}dy} = - 4\int\limits_{\sqrt 2 - 1}^1 {\ln \left( y \right)\sum\limits_{n = 0}^\infty {{{\left( { - 1} \right)}^n}{y^{2n}}} dy} = }$

$\displaystyle{ = - 4\sum\limits_{n = 0}^\infty {{{\left( { - 1} \right)}^n}\int\limits_{\sqrt 2 - 1}^1 {\ln \left( y \right){y^{2n}}dy} } = \mathop = \limits^{\sqrt 2 - 1 = a} = - 4\sum\limits_{n = 0}^\infty {{{\left( { - 1} \right)}^n}\left( { - \ln a\frac{{{a^{2n + 1}}}}{{2n + 1}} - \frac{1}{{{{\left( {2n + 1} \right)}^2}}} + \frac{{{a^{2n + 1}}}}{{{{\left( {2n + 1} \right)}^2}}}} \right)} }$

$\displaystyle{ \Rightarrow \boxed{\int\limits_0^{\pi /4} {\ln \left( {\frac{{1 + \sin \left( x \right)}}{{1 - \sin \left( x \right)}}} \right)dx} = 4\ln a\sum\limits_{n = 0}^\infty {{{\left( { - 1} \right)}^n}\frac{{{a^{2n + 1}}}}{{2n + 1}}} + 4\sum\limits_{n = 0}^\infty {{{\left( { - 1} \right)}^n}\frac{1}{{{{\left( {2n + 1} \right)}^2}}}} - 4\sum\limits_{n = 0}^\infty {{{\left( { - 1} \right)}^n}\frac{{{a^{2n + 1}}}}{{{{\left( {2n + 1} \right)}^2}}}} }}$ με $\displaystyle{{a = \sqrt 2 - 1}}$

Όμως $\displaystyle{\sum\limits_{n = 0}^\infty {\frac{{{{\left( { - 1} \right)}^n}{x^{2n + 1}}}}{{2n + 1}}} = \arctan x}$ http://en.wikipedia.org/wiki/List_of_ma ... cal_series , οπότε $\displaystyle{\boxed{\sum\limits_{n = 0}^\infty {\frac{{{{\left( { - 1} \right)}^n}{a^{2n + 1}}}}{{2n + 1}}} = \arctan \left( {\sqrt 2 - 1} \right) = \frac{\pi }{8}}}$

και $\displaystyle{\boxed{\sum\limits_{n = 0}^\infty {\frac{{{{\left( { - 1} \right)}^n}}}{{{{\left( {2n + 1} \right)}^2}}}} = G}}$ όπου

η σταθερά του Catalan με G = 0,915965594177...

http://en.wikipedia.org/wiki/Catalan%27s_constant

Επίσης $\displaystyle{\sum\limits_{n = 0}^\infty {\frac{{{{\left( { - 1} \right)}^n}{x^{2n + 1}}}}{{2n + 1}}} = \arctan x \Rightarrow \sum\limits_{n = 0}^\infty {\frac{{{{\left( { - 1} \right)}^n}{x^{2n}}}}{{2n + 1}}} = \frac{{\arctan x}}{x} \Rightarrow \sum\limits_{n = 0}^\infty {\frac{{{{\left( { - 1} \right)}^n}}}{{2n + 1}}\int\limits_0^a {{x^{2n}}dx} } = \int\limits_0^a {\frac{{\arctan x}}{x}dx} = \int\limits_0^{\sqrt 2 - 1} {\frac{{\arctan x}}{x}dx} }$ .

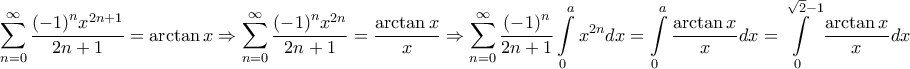και τελικά $\displaystyle{\boxed{\int\limits_0^{\pi /4} {\ln \left( {\frac{{1 + \sin \left( x \right)}}{{1 - \sin \left( x \right)}}} \right)dx} = \frac{\pi }{2}\ln \left( {\sqrt 2 - 1} \right) + 4G - 4\int\limits_0^{\sqrt 2 - 1} {\frac{{\arctan x}}{x}dx} }}$

-----------------------------------------------------------------------------------------------------------------------------------------------------------

Επειδή $\displaystyle{\int\limits_0^1 {\frac{{\arctan x}}{x}dx} = G\left( {Catalan} \right)}$ υποψιάζομαι ότι το ολοκλήρωμα $\displaystyle{{\int\limits_0^{\sqrt 2 - 1} {\frac{{\arctan x}}{x}dx} }}$ μπορεί να εκφραστεί συναρτήσει της

, δεν κατάφερα όμως να το υπολογίσω .. anyway .. που λέει κι ο φίλος μου ο Αναστάσης.

#6

http://www.mateforum.ro/viewtopic.php?t=4876

#7

Σεραφείμ έγραψε:για το ολοκλήρωμα $\displaystyle{{\int\limits_0^{\sqrt 2 - 1} {\frac{{\arctan x}}{x}dx} }}$

Μπορεί κανείς να δει και εδώ σελίδες 26-27. Δε φαίνεται να υπολογίζεται συναρτήσει γνωστών σταθερών.

Για την ιστορία το θέμα αυτό το είχαν βάλει στο mateforum στον κατάλογο με τα σχολικά, όπως φαίνεται και στο πάνω λινκ (και σημειωτέον ότι το έβαλε ο Cezar Lupu, που δεν έιναι και τυχαίος). Και έπειτα κάποιος άλλος ήρθε και το έβαλε εδώ... Πάλι καλά που δεν το έβαλε στα σχολικά κι αυτός... Anyway, τουλάχιστον έγινε κουβέντα.

Ολοκλήρωμα με λογάριθμο και ημίτονα

Ολοκλήρωμα με λογάριθμο και ημίτονα

Re: Ολοκλήρωμα με λογάριθμο και ημίτονα

Re: Ολοκλήρωμα με λογάριθμο και ημίτονα

Re: Ολοκλήρωμα με λογάριθμο και ημίτονα

Re: Ολοκλήρωμα με λογάριθμο και ημίτονα

Re: Ολοκλήρωμα με λογάριθμο και ημίτονα

Re: Ολοκλήρωμα με λογάριθμο και ημίτονα

Μέλη σε σύνδεση