 θετικός ακέραιος και
θετικός ακέραιος και ![f:[0,1] \to \mathbb{R} f:[0,1] \to \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/d961f003d1b32deb05785be107ca82fb.png) συνεχής συνάρτηση έτσι ώστε
συνεχής συνάρτηση έτσι ώστε  για κάθε
για κάθε  . Να δειχθεί ότι
. Να δειχθεί ότι 
Συντονιστής: Demetres
 βαθμού, έστω
βαθμού, έστω  τέτοιο ώστε
τέτοιο ώστε  για κάθε
για κάθε  .
.


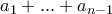
 (1)
(1) και το
και το  είναι
είναι  βαθμού άρα πρεπει
βαθμού άρα πρεπει  (2)
(2) και επιπλέον (συγκρίνοντας τους συντελεστές του
και επιπλέον (συγκρίνοντας τους συντελεστές του  έχουμε ότι
έχουμε ότι  άρα
άρα 

 ή ισοδύναμα
ή ισοδύναμα 
Κατά αρχάς υπάρχουν κάποια τυπογραφικά στην λύση του Σιλουανού.silouan έγραψε: ↑Τετ Ιαν 25, 2012 4:46 pmΞεθάβω αυτή τη λύση μου από το mathlinks από το 2008
Αναζητούμε πολυώνυμοβαθμού, έστω
τέτοιο ώστε
για κάθε
.
Οπότε καταλήγουμε στο σύστημα

...
...
...
Το σύστημα αυτό πρφανώς έχει λύση . Θα αναζητήσουμε τώρα το άθροισμα
Θεωρούμε το πολυώνυμο(1)
Από το σύστημα έχουμε ότικαι το
είναι
βαθμού άρα πρεπει
(2)
Εξισώνοντας τις (1),(2) βρίσκουμε ότικαι επιπλέον (συγκρίνοντας τους συντελεστές του
έχουμε ότι
άρα
Επίσης είναι
Τώρα έχουμεή ισοδύναμα









 έχω
έχω  .
.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες