Στην προσπάθεια για κάτι άλλο, κατέληξα στο παρακάτω. Το δίνω προς απόδειξη (ή απόρριψη, αν έχει γίνει λάθος στην απόδειξη που έκανα).
Να αποδειχθεί ή να απορριφτεί καθένας από τους παρακάτω ισχυρισμούς:
Έστω
 υποσύνολο του
υποσύνολο του  με κανένα σημείο συσσώρευσης.
με κανένα σημείο συσσώρευσης.1)Έστω τριώνυμο
 , με
, με  . Τότε, όλες οι πραγματικές ρίζες του
. Τότε, όλες οι πραγματικές ρίζες του  για τις διάφορες τιμές των
για τις διάφορες τιμές των  σχηματίζουν υποσύνολο του
σχηματίζουν υποσύνολο του  με κανένα σημείο συσσώρευσης.
με κανένα σημείο συσσώρευσης.2)Έστω πολυώνυμο
 , με
, με  .Τότε, όλες οι πραγματικές ρίζες του
.Τότε, όλες οι πραγματικές ρίζες του  για τις διάφορες τιμές των
για τις διάφορες τιμές των  σχηματίζουν υποσύνολο του
σχηματίζουν υποσύνολο του  με κανένα σημείο συσσώρευσης.
με κανένα σημείο συσσώρευσης.3)Έστω πολυώνυμο
 , με
, με  .Τότε, όλες οι πραγματικές ρίζες του
.Τότε, όλες οι πραγματικές ρίζες του  για τις διάφορες τιμές των
για τις διάφορες τιμές των  σχηματίζουν υποσύνολο του
σχηματίζουν υποσύνολο του  με κανένα σημείο συσσώρευσης.
με κανένα σημείο συσσώρευσης.
 και κάτω ίσους με το μηδέν).
και κάτω ίσους με το μηδέν). 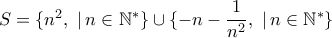 παρατηρούμε ότι τα στοιχεία του είναι διακριτά (απέχουν τουλάχιστον
παρατηρούμε ότι τα στοιχεία του είναι διακριτά (απέχουν τουλάχιστον  , οπότε δεν έχουν σ.σ.). Από την άλλη το πολυώνυμο
, οπότε δεν έχουν σ.σ.). Από την άλλη το πολυώνυμο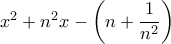

 , αληθεύουν οι ισχυρισμοί;
, αληθεύουν οι ισχυρισμοί; , πάλι οι ρίζες μπορεί να έχουν σημείο συσσώρευσης. Για παράδειγμα το πολυώνυμο
, πάλι οι ρίζες μπορεί να έχουν σημείο συσσώρευσης. Για παράδειγμα το πολυώνυμο έχει ρίζα
έχει ρίζα 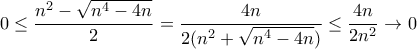
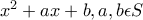 έχει το
έχει το  σημείο συσσώρευσης.
σημείο συσσώρευσης. όρων του
όρων του  ή
ή 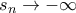 .
. , με ρίζα
, με ρίζα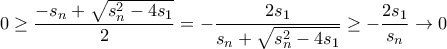 .
.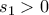 , αφού τελικά οι όροι της ακολουθίας είναι θετικοί.
, αφού τελικά οι όροι της ακολουθίας είναι θετικοί.