Να δειχθεί ότι σε τυχόν τρίγωνο
 ισχύει η ανισότητα
ισχύει η ανισότητα ![|AB|+|AC|\leq \dfrac{|BC|}{sin[(\angle BAC)/2]} |AB|+|AC|\leq \dfrac{|BC|}{sin[(\angle BAC)/2]}](/forum/ext/geomar/texintegr/latexrender/pictures/765408d6872d193bb497ecb93a3ec274.png) .
.[Ευχαριστώ τον Γιώργο Βισβίκη για διόρθωση στην φορά της ανισότητας!]
Συντονιστής: Παύλος Μαραγκουδάκης
 ισχύει η ανισότητα
ισχύει η ανισότητα ![|AB|+|AC|\leq \dfrac{|BC|}{sin[(\angle BAC)/2]} |AB|+|AC|\leq \dfrac{|BC|}{sin[(\angle BAC)/2]}](/forum/ext/geomar/texintegr/latexrender/pictures/765408d6872d193bb497ecb93a3ec274.png) .
. .
. .
. ,
,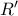 η ακτίνα του περιγεγραμμένου κύκλου του
η ακτίνα του περιγεγραμμένου κύκλου του  .
. είναι μικρότερη είτε ίση από τη διάμετρο του προαναφερθέντος κύκλου.
είναι μικρότερη είτε ίση από τη διάμετρο του προαναφερθέντος κύκλου. και του νόμου συνημιτόνων.
και του νόμου συνημιτόνων.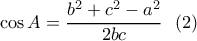

 .
. : Είναι
: Είναι  λόγω της τριγωνικής ανισότητας.
λόγω της τριγωνικής ανισότητας. και πολλαπλασιάζοντας με
και πολλαπλασιάζοντας με  τα 2 μέλη της ζητούμενης έχουμε διαδοχικά:
τα 2 μέλη της ζητούμενης έχουμε διαδοχικά:
 δηλαδή αν και μόνο αν
δηλαδή αν και μόνο αν  .
. είναι το έγκεντρο και
είναι το έγκεντρο και  η ακτίνα του εγγεγραμμένου κύκλου,
η ακτίνα του εγγεγραμμένου κύκλου, 
 , που ισχύει.
, που ισχύει. είναι και διχοτόμος δηλαδή όταν το τρίγωνο είναι ισοσκελές με βάση την
είναι και διχοτόμος δηλαδή όταν το τρίγωνο είναι ισοσκελές με βάση την  .
. το μέσο του τόξου
το μέσο του τόξου  του περιγεγραμμένου κύκλου.
του περιγεγραμμένου κύκλου. .
.Με
 έγκεντρο του
έγκεντρο του  από Van Aubel έχουμε
από Van Aubel έχουμε . Αλλά
. Αλλά 
 . Αρκεί λοιπόν :
. Αρκεί λοιπόν :  ,
, , η οποία ισχύει αφού το α' μέλος είναι το
, η οποία ισχύει αφού το α' μέλος είναι το  ,
,  , είναι
, είναι  , με την ισότητα αν
, με την ισότητα αν  ( ισοσκελές ) .
( ισοσκελές ) . με
με  ,
,  ,
,  , όπου
, όπου  ,
,  . Το πηλίκο
. Το πηλίκο 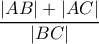 μπορεί λοιπόν να εφρασθεί ως συνάρτηση του
μπορεί λοιπόν να εφρασθεί ως συνάρτηση του  ,
,  . Ισχύει η
. Ισχύει η  , άρα το μέγιστο της
, άρα το μέγιστο της  επιτυγχάνεται σε ένα από τα άκρα του διαστήματος
επιτυγχάνεται σε ένα από τα άκρα του διαστήματος ![[0, 1] [0, 1]](/forum/ext/geomar/texintegr/latexrender/pictures/264884439b70ab09a86bc848421c6de6.png) . Εύκολα βλέπουμε ότι
. Εύκολα βλέπουμε ότι  , και αυτό μας οδηγεί στην (ανα)ζητούμενη ανισότητα.
, και αυτό μας οδηγεί στην (ανα)ζητούμενη ανισότητα. .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες