και το σχετιζόμενο θέμα της απαλοιφής .
Λοιπόν , να σχεδιαστεί ο γεωμετρικός τόπος των σημείων
 , αν:
, αν: 
Συντονιστής: Παύλος Μαραγκουδάκης
 , αν:
, αν: 
Για
 έχουμε το αποδεκτό σημείο
έχουμε το αποδεκτό σημείο 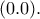 Έστω τώρα
Έστω τώρα  τότε, αν θέσουμε
τότε, αν θέσουμε 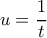 η "καμπύλη γράφεται":
η "καμπύλη γράφεται":  οπότε έχουμε:
οπότε έχουμε: 
Γεια σας και χρόνια πολλά! Να καταθέσω μία σκέψη: το σημείο του παραπάνω κύκλου με τετμημένη 1 (και τεταγμένη 0) νομίζω ότι εξαιρείται από τον ζητούμενο γεωμετρικό τόπο. Με πολλή εκτίμηση προς το πρόσωπό σας κύριε Λουρίδα!S.E.Louridas έγραψε: ↑Σάβ Δεκ 26, 2020 9:31 pmΓιαέχουμε το αποδεκτό σημείο
Έστω τώρα
τότε, αν θέσουμε
η "καμπύλη γράφεται":
οπότε έχουμε:

Προφανώς και έχεις απόλυτα δίκιο και σίγουρα χαίρομαι που το διαπίστωσες.left έγραψε: ↑Σάβ Δεκ 26, 2020 10:28 pmΓεια σας και χρόνια πολλά! Να καταθέσω μία σκέψη: το σημείο του παραπάνω κύκλου με τετμημένη 1 (και τεταγμένη 0) νομίζω ότι εξαιρείται από τον ζητούμενο γεωμετρικό τόπο. Με πολλή εκτίμηση προς το πρόσωπό σας κύριε Λουρίδα!S.E.Louridas έγραψε: ↑Σάβ Δεκ 26, 2020 9:31 pmΓιαέχουμε το αποδεκτό σημείο
Έστω τώρα
τότε, αν θέσουμε
η "καμπύλη γράφεται":
οπότε έχουμε:

 και
και 
Σας ευχαριστώ πολύ για την κατατοπιστική απάντηση, να είστε καλά!S.E.Louridas έγραψε: ↑Κυρ Δεκ 27, 2020 12:07 amΠροφανώς και έχεις απόλυτα δίκιο και σίγουρα χαίρομαι που το διαπίστωσες.left έγραψε: ↑Σάβ Δεκ 26, 2020 10:28 pmΓεια σας και χρόνια πολλά! Να καταθέσω μία σκέψη: το σημείο του παραπάνω κύκλου με τετμημένη 1 (και τεταγμένη 0) νομίζω ότι εξαιρείται από τον ζητούμενο γεωμετρικό τόπο. Με πολλή εκτίμηση προς το πρόσωπό σας κύριε Λουρίδα!S.E.Louridas έγραψε: ↑Σάβ Δεκ 26, 2020 9:31 pmΓιαέχουμε το αποδεκτό σημείο
Έστω τώρα
τότε, αν θέσουμε
η "καμπύλη γράφεται":
οπότε έχουμε:

Απλά δεν έδωσα πλήρως την λύση παρά μόνο μία τεχνική-σκέψη , ώστε να δούμε σε ποια καμπύλη ή γενικότερα ένωση σημειοσυνόλων ευρίσκονται τα σημεία του τόπου, χωρίς κατανάγκην να είναι όλα τα σημεία της καμπύλης ή της ένωσης των υποσυνόλων (με λίγα λόγια έμεινα στην Ανάλυση) για τούτο και οι τελίτσες. Προφανώς σε πλήρη λύση (που αποτελείται από τα βήματα: Ανάλυση-Σύνθεση-Απόδειξη-Διερεύνηση) θα πρέπει σίγουρα να βρούμε τα πεδία τιμών τωνκαι

 και
και 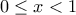 .
.  , γι'αυτό είχε προκύψει ημικύκλιο .
, γι'αυτό είχε προκύψει ημικύκλιο .Θανάση, νομίζω ο τόπος είναι όλος ο κύκλος (πλην του σημείου
 στο δεξί άκρο), όπως άλλωστε γράφουν οι παραπάνω.
στο δεξί άκρο), όπως άλλωστε γράφουν οι παραπάνω. . Tρόπος του λέγειν (αλλά μην με ψέξετε) είναι η περίπτωση
. Tρόπος του λέγειν (αλλά μην με ψέξετε) είναι η περίπτωση 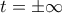 .
.Είναι άμεσο για κάποιον που γνωρίζει αυτό: https://en.m.wikipedia.org/wiki/Weierst ... bstitution
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης