cretanman έγραψε: ↑Τετ Ιούλ 18, 2018 11:54 pm
Υ.Γ. Ήμουν μαθητής στην Α Λυκείου εκείνη τη χρονιά...

.
Αλέξανδρε, για την ιστορία το θέμα αυτό (Θαλής, Α' Λυκείου 1996) το είχα τοποθετήσει o ίδιος ως μέλος της τότε Επιτροπής Διαγωνισμών της ΕΜΕ. Η κατασκευή του προήλθε από τα εξής:
Δίδασκα εκείνο το εξάμηνο ένα μάθημα στο Μαθηματικό Κρήτης με τίτλο Θεωρητική Αριθμητική Ανάλυση. Αφού συζητήσαμε την απόσταση σημείων ως προς διάφορες νόρμες του

φτάσαμε και στο παραπάνω παράδειγμα, του οποίου η περίπτωση της νόρμας

είναι γνωστή. Πρόκειται για την απόσταση ελάχιστων τετραγώνων (least squares distance). Αναρωτήθηκα λοιπόν τι γίνεται με την περίπτωση της νόρμας
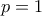
, και χάρηκα όταν διαπίστωσα ότι έχει ωραία απάντηση. Από εκεί ορμώμενος το πρότεινα ως θέμα στον ΘΑΛΗ.
Η λύση που έδωσα για τον διαγωνισμό είναι αυτή του αναφέρεις. Στους φοιτητές όμως έδωσα και την εξής δεύτερη λύση.
Εξετάζουμε το γράφημα της

. Αφού

είναι άμεσο το γράφημα αποτελείται από ευθύγραμμα τμήματα με άκρα στα σημεία με

. Οι κλίσεις των ευθυγράμμων τμημάτων είναι

, δηλαδή ακέραιοι, ακριβέστερα περιττοί αν τα σημεία είναι περιττό πλήθος, και άρτιοι αλλιώς. Τα σχήματα παρακάτω είναι δύο ενδεικτικές περιπτώσεις, με 5 και με 6 σημεία, αντίστοιχα.
Από το σχήμα διαβάζουμε το ελάχιστο. Στην περίπτωση περιττού πλήθους είναι στο μεσαίο σημείο, αλλιώς είναι σε ολόκληρο διάστημα.
 διακεκριμένα σημεία
διακεκριμένα σημεία  πάνω σε μια ευθεία. Να βρεθεί σημείο
πάνω σε μια ευθεία. Να βρεθεί σημείο  της ευθείας για το οπoίο πετυχαίνουμε το
της ευθείας για το οπoίο πετυχαίνουμε το 
 διακεκριμένα σημεία
διακεκριμένα σημεία  πάνω σε μια ευθεία. Να βρεθεί σημείο
πάνω σε μια ευθεία. Να βρεθεί σημείο  της ευθείας για το οπoίο πετυχαίνουμε το
της ευθείας για το οπoίο πετυχαίνουμε το 
 από κάθε σημείο
από κάθε σημείο  . Αν τα σημεία είναι 2
. Αν τα σημεία είναι 2  τότε το ελάχιστο άθροισμα δίνεται από κάθε σημείο
τότε το ελάχιστο άθροισμα δίνεται από κάθε σημείο  ίσο με την απόσταση αυτών. Αν
ίσο με την απόσταση αυτών. Αν  με έστω το τρίτο σημείο εντός του διαστήματος
με έστω το τρίτο σημείο εντός του διαστήματος ![\left [ a_1, a_2 \right ] \left [ a_1, a_2 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/1a423b68cfd120c916fbcfc3efe6a06e.png) τότε έχουμε ελάχιστο για
τότε έχουμε ελάχιστο για  . Αν
. Αν  με διάταξη έστω
με διάταξη έστω  τότε το ελάχιστο προκύπτει για κάθε σημείο
τότε το ελάχιστο προκύπτει για κάθε σημείο ![\left [ a_2, a_3 \right ] \left [ a_2, a_3 \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/fd0ca7838450623183240c2721e90a12.png) . Ουσιαστικά μιλάμε για το median των τιμών
. Ουσιαστικά μιλάμε για το median των τιμών  που είναι το μεσαίο σε διάταξη σημείο αν
που είναι το μεσαίο σε διάταξη σημείο αν  (και όμοια για οποιοδήποτε περιττό) η απόδειξη είναι εδώ
(και όμοια για οποιοδήποτε περιττό) η απόδειξη είναι εδώ  φτάσαμε και στο παραπάνω παράδειγμα, του οποίου η περίπτωση της νόρμας
φτάσαμε και στο παραπάνω παράδειγμα, του οποίου η περίπτωση της νόρμας  είναι γνωστή. Πρόκειται για την απόσταση ελάχιστων τετραγώνων (least squares distance). Αναρωτήθηκα λοιπόν τι γίνεται με την περίπτωση της νόρμας
είναι γνωστή. Πρόκειται για την απόσταση ελάχιστων τετραγώνων (least squares distance). Αναρωτήθηκα λοιπόν τι γίνεται με την περίπτωση της νόρμας 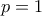 , και χάρηκα όταν διαπίστωσα ότι έχει ωραία απάντηση. Από εκεί ορμώμενος το πρότεινα ως θέμα στον ΘΑΛΗ.
, και χάρηκα όταν διαπίστωσα ότι έχει ωραία απάντηση. Από εκεί ορμώμενος το πρότεινα ως θέμα στον ΘΑΛΗ. . Αφού
. Αφού  είναι άμεσο το γράφημα αποτελείται από ευθύγραμμα τμήματα με άκρα στα σημεία με
είναι άμεσο το γράφημα αποτελείται από ευθύγραμμα τμήματα με άκρα στα σημεία με  . Οι κλίσεις των ευθυγράμμων τμημάτων είναι
. Οι κλίσεις των ευθυγράμμων τμημάτων είναι  , δηλαδή ακέραιοι, ακριβέστερα περιττοί αν τα σημεία είναι περιττό πλήθος, και άρτιοι αλλιώς. Τα σχήματα παρακάτω είναι δύο ενδεικτικές περιπτώσεις, με 5 και με 6 σημεία, αντίστοιχα.
, δηλαδή ακέραιοι, ακριβέστερα περιττοί αν τα σημεία είναι περιττό πλήθος, και άρτιοι αλλιώς. Τα σχήματα παρακάτω είναι δύο ενδεικτικές περιπτώσεις, με 5 και με 6 σημεία, αντίστοιχα.