Ανισότητα με συνάρτηση!

#1

Αν $\displaystyle{f(x)=\frac{x-1}{\ln x}, ~~0<x\ne 1}$ , να αποδείξετε ότι

$\displaystyle{f(a^2)+f(b^2)\geq 2f(ab)}$

για οποιαδήποτε $\displaystyle{a,b\in(0,1)\cup (1,+\infty),}$ με $\displaystyle{ab\ne 1.}$

Την παραπάνω ανισότητα την κατασκεύασα με τρόπο, ο οποίος δεν φαίνεται να οδηγεί σε επέκταση σε περισσότερες από δύο μεταβλητές.
Υπάρχει άραγε τέτοια επέκταση;

#2

matha έγραψε: ↑
Κυρ Ιουν 17, 2018 1:40 pm
Αν $\displaystyle{f(x)=\frac{x-1}{\ln x}, ~~0<x\ne 1}$ , να αποδείξετε ότι

$\displaystyle{f(a^2)+f(b^2)\geq 2f(ab)}$

για οποιαδήποτε $\displaystyle{a,b\in(0,1)\cup (1,+\infty),}$ με $\displaystyle{ab\ne 1.}$

Την παραπάνω ανισότητα την κατασκεύασα με τρόπο, ο οποίος δεν φαίνεται να οδηγεί σε επέκταση σε περισσότερες από δύο μεταβλητές.
Υπάρχει άραγε τέτοια επέκταση;

Προς το παρόν δεν την βλέπω την επέκταση, καθώς η

δεν είναι κυρτή

Για την περίπτωση των δύο μεταβλητών όπως τέθηκε παραπάνω ... εύλογα υποθέτω $b\geq a$ και θεωρώ την g(b)=f(a^2)+f(b^2)-2f(ab)

. Αρκεί, λόγω g(a)=0

, να δειχθεί η g'(b)>0

για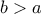

, αρκεί δηλαδή να δειχθεί η bf'(b^2)>af'(ab)

, για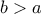

πάντοτε. Ύστερα από λίγες πράξεις παρατηρούμε ότι η ζητούμενη ανισότητα είναι ισοδύναμη προς την

$\dfrac{b^2ln(b^2)-b^2+1}{(ln(b^2))^2}>\dfrac{(ab)ln(ab)-(ab)+1}{(ln(ab))^2},$

όπου, από b>a

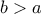, έχουμε

. Αρκεί δηλαδή να δειχθεί ότι είναι αύξουσα η $h(y)=\dfrac{ylny-y+1}{(lny)^2}$ . Ισχύει η

$h'(y)=\dfrac{y(lny)^2-2ylny+2y-2}{(lny)^3},$

οπότε, επειδή χρειαζόμαστε την $h'(y)\geq0$ και ο αριθμητής της h'(y)

μηδενίζεται για y=1

ενώ ο παρονομαστής της h'(y)

αλλάζει πρόσημο στο y=1

, αρκεί να δειχθεί ότι ο αριθμητής είναι αύξουσα συνάρτηση του

, κάτι που προκύπτει από την (y(lny)^2-2ylny+2y-2)'=(lny)^2>0

.

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ · #3

matha έγραψε: ↑
Κυρ Ιουν 17, 2018 1:40 pm
Αν $\displaystyle{f(x)=\frac{x-1}{\ln x}, ~~0<x\ne 1}$ , να αποδείξετε ότι

$\displaystyle{f(a^2)+f(b^2)\geq 2f(ab)}$

για οποιαδήποτε $\displaystyle{a,b\in(0,1)\cup (1,+\infty),}$ με $\displaystyle{ab\ne 1.}$

Την παραπάνω ανισότητα την κατασκεύασα με τρόπο, ο οποίος δεν φαίνεται να οδηγεί σε επέκταση σε περισσότερες από δύο μεταβλητές.
Υπάρχει άραγε τέτοια επέκταση;

Νομίζω ότι η απόδειξη του Γιώργου δίνει την ανισότητα και στην περίπτωση που

$\displaystyle{a,b\in (0,+\infty)}$

Ο λόγος είναι ότι αν θέσουμε f(1)=1

τότε η

είναι τουλάχιστον δυο φορές παραγωγίσιμη στο

$\displaystyle{ (0,+\infty)}$

Συμπλήρωμα .Η η

είναι άπειρες φορές παραγωγίσιμη στο

$\displaystyle{ (0,+\infty)}$

#4

Θεωρώ την συνάρτηση $g:\mathbb{R} \to \mathbb{R}$ με τύπο $\displaystyle g(x) = f(e^x) = \frac{e^x-1}{x}$ για $x \neq 0$ και g(0) = 1

. Η

είναι κυρτή (*) οπότε από Jensen έχουμε $\displaystyle \frac{g(x_1) + \cdots + g(x_n)}{n} \geqslant g\left( \frac{x_1 + \cdots + x_n}{n}\right)$

Θέτoντας $y_i = e^{x_i}$ παίρνω:

$\displaystyle f(y_1^n) + \cdots + f(y_n^n) = g(nx_1) + \cdots + g(nx_n) \geqslant ng\left( x_1 + \cdots + x_n\right) = nf(y_1\cdots y_n)$

(*) Έχουμε $\displaystyle g''(x) = \frac{e^x(x^2-2x+2)-2}{x^3}$ οπότε αρκεί να δείξουμε ότι η h(x) = e^x(x^2-2x+2)-2

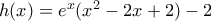είναι θετική για x>0

και αρνητική για x < 0

. Όμως

. Άρα η

είναι γνησίως αύξουσα και επειδή h(0) = 0

το ζητούμενο έπεται. [Χρειάζεται λίγη προσοχή με τις παραγώγους του

στο

. Αν κοιτάξουμε το ανάπτυγμα Taylor παρατηρούμε ότι δεν υπάρχει κάποιο πρόβλημα με αυτές τις παραγώγους και την ύπαρξη/συνέχειά τους στο

.]

Ανισότητα με συνάρτηση!

Ανισότητα με συνάρτηση!

Re: Ανισότητα με συνάρτηση!

Re: Ανισότητα με συνάρτηση!

Re: Ανισότητα με συνάρτηση!

Μέλη σε σύνδεση